Introduction :
Dans les transceivers des radioamateurs, les électroniques analogiques ont été de plus en plus remplacées depuis des années par des circuits numériques. Les premiers DSP (Digital Signal Processor) ont commencé leur apparition dans les maillons de la chaîne basse fréquence des récepteurs et leur utilisation s’est ensuite étendue jusqu’à la sortie des mélangeurs de la moyenne fréquence (MF). Il y avait donc une dernière étape à franchir : celle de raccorder l’entrée d’un circuit numérique directement à l’antenne d’émission-réception HF et de raccorder une sortie BF à un haut-parleur et une entrée à un microphone.
Les circuits logiques et numériques ont depuis longtemps la faculté d’être programmables et les progrès de l’informatique ont permis de créer des applications logicielles permettant à l’utilisateur de dialoguer avec un ensemble de circuits numériques préprogrammés. Une radio logicielle (SDR : Software Defined Radio) est donc constituée d’un ensemble de circuits numériques préprogrammés (paramétrés) réalisant des fonctions définies auxquelles l’utilisateur n’a pas l’accès, mais en revanche celui-ci peut en exploiter les fonctions grâce à une application logicielle.
Définition du terme « système de radiocommunication défini par logiciel (SDR) » par l’UIT (Union Internationale des Télécommunications), recommandation SM.2152-0 :
«Système de radiocommunication défini par logiciel (SDR) : émetteur et/ou récepteur de radiocommunication utilisant une technologie qui permet de régler ou de modifier au moyen d'un logiciel les paramètres d'exploitation RF, par exemple la gamme de fréquences, le type de modulation ou la puissance de sortie (la liste n'est pas exhaustive), à l'exclusion de modifications des paramètres d'exploitation qui interviennent pendant l'exploitation normale préinstallée et prédéterminée d'un appareil de radio conformément à une norme ou à une spécification de système».
Le domaine du numérique exige une nouvelle manière de réfléchir :
Les changements de l’analogique vers le numérique demandent de nouvelles adaptations quant à notre manière de réfléchir, autrement dit on ne peut plus raisonner en numérique comme on le faisait en analogique. Nous le verrons plus loin par exemple avec les convertisseurs analogiques-numériques (ADC : Analog to Digital Converter).
L’architecture elle-même de la partie réceptrice d’un transceiver SDR à conversion directe est complètement différente de celle d’un récepteur basé sur le principe du superhétérodyne avec plusieurs changements de fréquence. Ce n’est donc plus la peine d’essayer de tester les réjections des Fréquences Intermédiaires car il n’y a plus de FI analogique !
Principe de la conversion directe :
Le principe de la conversion directe dans un récepteur est de translater le contenu d’une modulation située sur une fréquence porteuse directement sur ce qu’on appelle la bande de base, c’est-à-dire la bande de fréquence strictement nécessaire occupée par un signal modulé ou parfois tout simplement la bande passante du signal « modulant » sans que celui-ci ne soit situé sur une fréquence porteuse. Pour un signal dit « en bande de base » (Baseband), tout se passe comme si ce signal n’avait pas subi à l’origine une transposition en fréquence, autrement dit après la conversion directe d’un récepteur, dans le signal en bande de base, il n’y a plus de HF ni de MF ni de FI. Dans le principe de la conversion directe d’un récepteur on parlera même de Zéro FI (ZIF : Zero Intermediate Frequency).
Le principe de la conversion directe dans un émetteur est de translater le contenu du signal en bande de base directement sur une porteuse HF. Voici donc deux exemples qui nous amènent à adopter une nouvelle manière de réfléchir dans le domaine du numérique des SDR.
Dans un transceiver SDR à conversion directe, la translation du signal HF modulé vers la bande de base en réception et la translation du signal modulant en bande de base vers un signal HF en émission s’effectuent toutes deux exclusivement par des circuits numériques préprogrammés. La translation en fréquence dans un récepteur s’effectuera par un convertisseur numérique abaisseur de fréquence qui est appelé Digital Down Converter (DDC) et la translation en fréquence dans un émetteur s’effectuera par un convertisseur numérique élévateur de fréquence qui est appelé Digital Up Converter (DUC). Les deux fonctions DDC et DUC sont réalisées dans un circuit numérique programmé et ultra rapide du type FPGA (Field-Programmable Gate Array) qui peut effectuer des opérations avec une fréquence d’horloge de base de temps très élevée.
Décimation et interpolation :
Dans un récepteur SDR, le DDC nécessite une fréquence d’horloge très élevée pour pouvoir effectuer une conversion à partir du signal HF. Lorsqu’on a obtenu le signal en bande de base, celui-ci est traité par un DSP qui va réaliser les fonctions de filtrage et de démodulation avec une vitesse d’horloge beaucoup plus faible que celle du FPGA. On passe donc d’un signal HF numérisé au moyen d’un nombre élevé d’échantillons par unité de temps au niveau du FPGA vers un signal en bande de base qui doit comporter beaucoup moins d’échantillons par unité de temps pour que celui-ci puisse être traité par un DSP. Cette réduction d’échantillonnage (Down-Sampling) s’effectue par un procédé appelé décimation qui consiste à traiter un seul échantillon parmi plusieurs, par exemple un sur 4 ou un sur 10, etc. La vitesse d’échantillonnage ainsi réduite correspond à celle qui est strictement nécessaire pour traiter un signal en bande de base dont l’étendue ne dépasse pas celui des « basses » fréquences.
Dans un émetteur SDR, le signal en bande de base est traité avec une faible vitesse d’échantillonnage par le DSP. En revanche, le DUC nécessite un échantillonnage à haute vitesse pour être compatible avec les fréquences HF.
On va rajouter de toutes pièces un nombre fixe d’échantillons entre ceux qui existent à la sortie du DSP pour atteindre l’échantillonnage requis par le DUC, il s’agit donc d’une élévation d’échantillonnage (Up-Sampling). Cette opération est appelée interpolation.
Qu’est-ce qu’un FPGA (Field-Programmable Gate Array) ?
Il s’agit d’un circuit intégré électronique qui est constitué de réseaux de portes logiques (Gate Array) qui peuvent être « câblées » et « re-câblées » entre elles à volonté par une programmation sur le terrain (Field Programmable), c’est-à-dire dans n’importe quel laboratoire d’électronique au moyen d’un ordinateur. La programmation va réaliser le « câblage » (routage) entre les portes logiques de façon à réaliser des fonctions logiques combinatoires ou séquentielles. La programmation va aussi déterminer l’emplacement des portes logiques d’une manière rationnelle sur la puce (Chip) du FPGA.
Grâce à un circuit composé de plusieurs blocs de portes logiques (CLB : Configurable Logic Block), on pourra ainsi réaliser en nombres binaires des opérations d’addition, de soustraction, de multiplication, de division, d’élévation au carré, d’extraction de racine carrée, de calcul d’arc-tangente et même de logarithme. On pourra aussi réaliser des opérations sur des nombres complexes en traitant leur partie réelle et leur partie imaginaire ou en traitant leur module et leur argument. En agissant par calcul sur l’argument d’un nombre complexe, cela revient à effectuer un déphasage constant sur un signal quelle que soit sa fréquence, ce qui est parfaitement impensable conceptuellement avec un circuit analogique à large bande. Tout ceci va être particulièrement précieux pour effectuer une conversion directe (DDC ou DUC) par calculs purement mathématiques sur des nombres complexes en traitant des signaux en quadrature de phase (déphasés de 90 °) sur le principe du mélangeur I et Q (I = In-Phase et Q = Quadrature-Phase). Le principe d’un mélangeur I et Q sera examiné plus loin.
Contrairement aux autres circuits intégrés du type ASIC (Application Specific Integrated Circuit), PAL (Programmable Array Logic), GAL (Gate Array Logic), etc., les FPGA peuvent être reprogrammés à volonté. Le langage de programmation des FPGA est adapté à la méthodologie de conception de circuits en logique « câblée » (par programmation) et met directement en œuvre des équations booléennes (algèbre des portes logiques) sans devoir passer par l’analyse des tables de vérité. Deux langages principaux existent (HDL : Hardware Description Langage) : VHDL pour les VHSIC (Very-High-Speed Integrated Circuit) et Verilog. Ces langages sont relativement complexes et peuvent paraître aussi rébarbatifs que du langage Assembleur. National Instruments a dès lors développé un module spécifique pour de la programmation HDL sous forme graphique dans son logiciel Lab View. La programmation HDL peut aussi être effectuée par l’intermédiaire des langages usuels d’informaticiens tels que C, C++, Python ou C# (C Sharp) avec des boites d’outils où certains « composants » ont été développés (Framework), comme par exemple avec Microsoft DotNet. Le logiciel Math Lab peut effectuer des simulations de programmations en HDL.
Le programme est ensuite compilé par des logiciels appropriés à la programmation des FPGA.
Le fichier de programmation du FPGA est transféré dans celui-ci par l’intermédiaire d’une interface série appelée JTAG (Joint Test Action Group). Historiquement, cette appellation provient du groupe de travail qui a conçu la norme IEEE 1149.1 qui définit un standard de port d’accès à des circuits numériques programmables de façon à tester les connexions qui relient les broches des différents circuits intégrés sur un circuit imprimé. Cette norme a été développée pour le test automatique des cartes électroniques à haute intégration de circuits numériques dans l’industrie (Standard Test Access Port and Boundary-Scan Architecture).
Les opérations mathématiques effectuées par un FPGA sont pratiquement réalisées en temps réel (il faut juste tenir compte du temps de propagation des états logiques des portes), ce qui rend ces dispositifs bien plus rapides que les microprocesseurs qui doivent effectuer des opérations arithmétiques et logiques (ALU : Arithmetic Logic Unit) une par une et d’une manière purement séquentielle en scrutant les instructions d’un programme informatique.
Les FPGA se sont complexifiés d’années en années à telle enseigne qu’ils intègrent actuellement non seulement des réseaux de portes logiques, mais aussi plusieurs « tranches » (Slice) avec des DSP et même un microprocesseur rapide grâce à un jeu minimal d’instructions (RISC : Reduced Instruction Set Computer). Ces « noyaux durs » (Hard-Core) à microprocesseurs RISC sont souvent du type d’architecture ARM (Advanced Risc Machine). Les ARM sont conçus depuis 1987 par la société britannique Acorn Computers devenue ARM Limited. Les FPGA avec noyau dur ARM deviennent des « systèmes sur puce » à part entière (SoC : System on Chip). On prendra pour exemple les SoC FPGA « Virtex » et « Zynq » conçus par la société Xilinx. Le FPGA Zynq dédié RFSoC (Radio Frequency System on Chip) intègre quatre processeurs (Quad Core) ARM « Cortex A-53 » et en plus deux processeurs (Dual Core) « Cortex R-5 ».
Les transceivers SDR du constructeur Flex Radio de la série 6000 Signature utilisent un FPGA Virtex-6 de la société Xilinx et un DSP de technologie « DaVinci » (Digital Multimedia Processing) de la société Texas Instruments. Les DSP DaVinci (alias de Digital Video) sont des SoC qui intègrent un processeur ARM.
Tables de correspondance (LUT : Look-Up Table) :
Certaines fonctions mathématiques, par exemple les fonctions trigonométriques, les logarithmes, etc. ne peuvent être calculées par les microprocesseurs ou par un réseau de portes logiques que par une décomposition en série d’opérations simples d’addition de plusieurs termes pour arriver au résultat. Ces décompositions en séries ont été découvertes par les mathématiciens Taylor, Mac Laurin et Riemann. Voici un exemple :
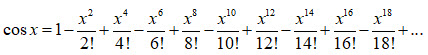
Pour arriver à une précision suffisante du résultat du calcul d’une fonction trigonométrique, le microprocesseur ou le FPGA doit procéder à un nombre élevé d’itérations afin de calculer un grand nombre de termes de la décomposition en série de cette fonction. Le nombre de cycles des calculs prennent donc beaucoup de temps pour être accomplis. C’est la raison pour laquelle les valeurs des fonctions trigonométrique sont pré-encodées dans une table mémoire du FPGA. Parmi nos aînés, certains OM se souviendront avoir utilisé des tables de logarithmes à l’école avant que les calculatrices de poche aient fait leur apparition dans l’enseignement.
Comme on ne peut pas raisonnablement encoder un nombre infini de valeurs dans une table mémoire, on choisit d’en encoder un nombre limité. Pour arriver à un résultat
de calcul qui se trouverait entre deux valeurs de la table, on procède à une interpolation mathématique, ce qui est une tâche facile à accomplir par un microprocesseur ou un FPGA.
Afin de réduire le nombre de valeur dans une table de correspondance, certaines fonctions trigonométriques peuvent être caractérisées seulement par un quart de leur domaine de définition. Par exemple un cosinus peut être défini pour des variables dont les valeurs sont comprises entre 0 et π/2. Entre π /2 et π, on retrouve les mêmes valeurs mais de manière croissante (en valeur absolue) et affectées du signe négatif.
Entre π et 3 π /2 ainsi qu’entre 3 π /2 et 2 π, les valeurs sont aussi des répliques de celles de l’intervalle compris entre 0 et π /2. Pour accéder aux valeurs des fonctions trigonométriques, la table est adressée au moyen d’un multiplexeur, un compteur ou un registre. Certaines tables de vérité de fonctions logiques complexes peuvent aussiêtre encodées dans des LUT (Look-Up Table) d’un FPGA afin d’optimiser les ressources de celui-ci.
FIN DE L'EXTRAIT
Ceci était l'introduction de mon article « SDR à conversion numérique directe : comment fonctionne ce qui est dans la boite noire et comment évaluer les performances ».
Commentaires :
Bonjour Cher OM,
Bravo pour ce travail de synthèse en français que vous venez de réaliser.
73 Jean-Louis F5CTP
Cet article peut être téléchargé au format PDF. Il suffit de cliquer sur ce lien :