Ferrites, ununs et baluns

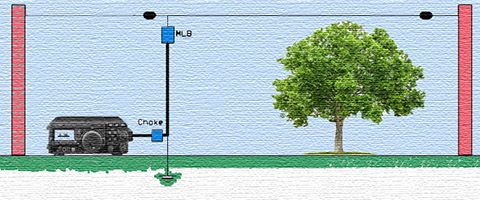
Les baluns et ununs constituent un sujet qui passionne beaucoup d’OMs et en rebute tout autant d’autres. Pourtant, rarement un sujet n’a été traité aussi empiriquement !
En effet, chacun reprend les travaux des autres et les erreurs prolifèrent au point que plus personne ne se pose de question. Le plus bel exemple en est le balun réalisé sur un tore T200­2 d’Amidon avec deux ou trois fois 9 spires. Son rendement est déplorable sur les bandes basses et personne ne s’en inquiète, semble-t-­il ! On attribue cela l’antenne ou à  d’autres facteurs. Mais si on se donne la peine de faire les calculs d’inductance et de réactance, à l’aide de MiniRK, par  exemple http://www.dl5swb.de/html/mini_ring_core calculator.htm, on s’aperçoit que la réactance est seulement de 22 Ω sur 80m et de 11 Ω sur 160m ! Et le TX est sensé « voir » une charge de 50 Ω… Or sur 40m, il ne voit encore que 44 Ω. Et à cela, il faut mettre l’impédance de l’antenne en parallèle.
A votre avis, qu’est ­ce que la boîte de couplage accorde en réalité ? Voilà pourquoi il faut un T200 (2" ou 50mm) alors qu’un FT140­61 (1,4" ou 36mm) serait bien suffisant.
Il y a une réalisation commerciale basé sur ce tore mais elle comporte 14 spires pour 50 ohms, soit 51 ohms sur 80m. Pas suffisant. En principe, il faut 10 fois l’impédance de charge sur la fréquence la plus basse, soit 500 Ω. Cela voudrait dire … 44 spires pour 50 Ω !!! Donc un magnetic balun devrait comporter plus de 130 spires pour descendre au 160m et 60 spires pour couvrir le 80m… Impensable car il ne monterait pas plus haut que le 20m du fait des résonances parasites.
Nous en verrons un exemple plus loin. Néanmoins, l’expérience montre qu’on peut accepter une réactance égale à 5 fois l’impédance de charge. C’est ainsi qu’avec un tore T140­61, trois fois 10 spires (réactance de 300 Ω sur 80m) suffisent pour couvrir du 80 au 10m avec un ROS <1,5:1. En réception son fonctionnement est acceptable et suffisant pour couvrir une plage allant de 100KHz à 50MHz En effet, la puissance des émetteurs P.O. et G.O. est très élevée et le QRN en est au prorata. La sensibilité requise est donc bien moindre qu’en décamétrique.

Tests

Un balun ou un unun se teste comme n’importe quel autre circuit HF passif : avec un TX, un ROS­mètre et une résistance ohmique. Il suffira de lui souder une résistance égale à la valeur de la charge qu’il est sensé recevoir et de le raccorder à un TX via un ROS­mètre. Bien entendu un analyseur d’antenne sera d’une aide bien plus précieuse encore, mais tous les OMs n’en possèdent pas car il faut en avoir une utilité suffisante.

Les résistances de charge

200 Ω (balun ou unun 4:1) :
deux résistances de 100 Ω­ 2W­ en série ou quatre fois deux résistances de 100 Ω, 1W ou plus, en parallèle ; les quatre groupes sont, à leur tour, montés en série. Dans le premier cas, il faut choisir des résistances métal­-film de 2W. La seconde version s’impose si vous ne pouvez en trouver que de 1W.

300 Ω (balun 6:1 pour Windom ou T2FD) :
quatre fois deux résistances de 150 Ω.

450 Ω (unun 9:1 ou MLB) :
trois résistances de 150 Ω en série ou quatre résistances de 1800 Ω en parallèle, 2W si possible.

La mesure

Réglez votre TX pour qu’il donne la puissance la plus faible possible, 5W s’il l’accepte. Sinon, commutez-­le en AM : la porteuse a, généralement, le quart de la puissance PEP ou CW.
N’ayez pas peur d’appliquer une puissance un peu supérieure à la dissipation totale des résistances : elles chaufferont et peuvent même aller jusqu’à se dessouder mais cela est sans danger pour les « métal film » qui le supporteront bien.
N’appliquez toutefois la puissance que le temps strictement nécessaire à la mesure et laissez refroidir quelques dizaines de secondes si c’est vraiment très chaud.
Mesurez alors le TOS comme pour une antenne normale. Répétez la mesure pour le milieu de chaque bande WARC (c’est suffisant) et notez ­là.
Si le TOS est élevé sur 160 ou 80m, et très faible sur 10m , ajoutez une ou deux spires. Si c’est le contraire, retirez des spires. L’idéal est d’avoir une courbe de réponse équilibrée.
Si vous voulez un ROS proche de 1:1 sur vos bandes de prédilection, il faudra procéder de même.

Les caractéristiques d’un tore

En plus de ses dimensions physiques, un tore possède des propriétés magnétiques. Le magnétisme est une matière très complexe, avec de nombreux paramètres. Pour la ferrite et la poudre de fer, les fabricants donnent des courbes de caractéristiques majoritairement obtenues par mesure et expérimentation car il n’y a pas beaucoup de règles mathématiques absolues qui s’appliquent à ces matériaux.

La perméabilité

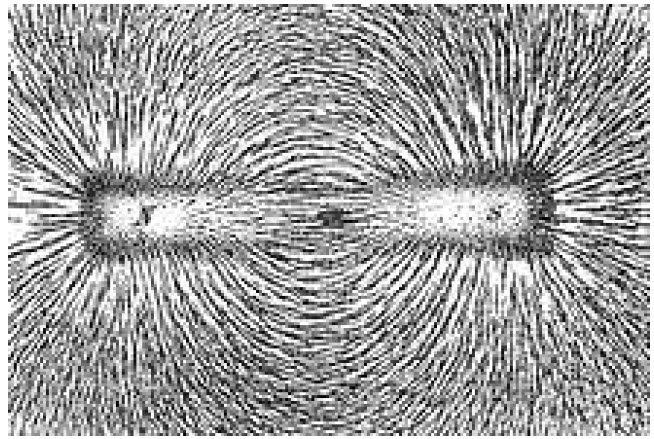
Illustration de Wikipédia

La perméabilité est la propriété d’un corps à capturer ces lignes de champ et à les maintenir en son sein. Chaque spire d’un bobinage génère un champ magnétique qui est induit dans les autres spires (c’est pour cela que l’inductance est proportionnelle au carré du nombre de spires). Mais les lignes de champ qui sont en dehors du noyau ou du centre du bobinage n’ont que peu d’effet. Par contre, un tore en maintient un maximum (dépendant de sa perméabilité) dans sa matière, au grand bénéfice des autres spires.
Lorsque vous approchez l’un de l’autre deux bobinages sur air ou sur mandrin, vous avez un couplage. Sur tore, ce couplage est inexistant car les lignes de champ ne circulent pratiquement pas en dehors. C’est pour cela qu’il est possible de mettre deux bobinages sur tore à proximité l’un de l’autre sans interférence (on ne doit plus court-circuiter le bobinage inutilisé). Voyez les coupleurs automatiques et les filtres de sortie d’un TX. Et c’est aussi pour cela qu’il est quasiment impossible de mesurer un circuit oscillant sur tore à l’aide d’un grid-­dip.

La saturation

C’est comme pour l’eau dans un tuyau : il y a un moment où la matière magnétique ne peut plus admettre plus de lignes de champ, le tuyau est plein. A ce moment ­là, tout ce qui dépasse une certaine tension est écrêté, comme avec un clipper, et cela engendre des harmoniques. On le voit parce que le TOS augmente. Cela se produit instantanément.
Avec la ferrite, la puissance admissible est toujours limitée par la saturation qui est déterminée par la tension appliquée et non par le courant, comme on le croit souvent.
Avec la poudre de fer, c’est souvent l’élévation de température qui limite la puissance.

Les pertes

Lorsque vous glissez une tige d’acier dans un solénoïde (= une bobine de fil de cuivre) et que vous y appliquez une tension, le métal s’aimante et reste aimanté par la suite. Pour le désaimanter, il faut appliquer le courant en sens inverse.
La ferrite et la poudre de fer (les FTxx­yy et Txx­y de chez Amidon) souffrent toutes deux du même phénomène mais à un niveau extrêmement faible. En cas de courant alternatif, une alternance magnétise le noyau dans un sens, l’autre alternance le magnétise dans l’autre sens. Mais avant de magnétiser dans l’autre sens, il faut d’abord ramener l’aimantation à zéro et tout cela implique une dépense d’énergie qui se traduit en chaleur. C’est pour cette raison que les fils employés dans les baluns et ununs sont gainés téflon.
Dans un noyau parfait, l’aimantation suivrait fidèlement la sinusoïde, sans rémanence.
L’autre type de perte significatif est « l’effet four à micro­ ondes » : la HF fait chauffer la matière et cet effet se fait sentir de manière croissante à mesure que la fréquence augmente.

Effet de la température

Les pertes dans le tore convertissent l’énergie en chaleur. Passé une certaine température (allant de 120 à 300°), la matière atteint un état paradoxal où sa perméabilité disparaît.
C’est le point de Curie. Un autre paradoxe est que la perméabilité augmente avec la température avant de s’effondrer littéralement. Cela se voit aussi au ROS­mètre car le TOS grimpe d’un coup à une valeur très élevée. Ce phénomène se produit après un temps d’émission plus ou moins long et se manifeste surtout en RTTY, PSK, FM, etc.
Cela peut conduire à la destruction du tore qui se casse en morceaux !

La courbe de réponse d’un bobinage sur tore

Sur 80m, c’est la ferrite qui gère tout. Sur 6m, elle n’a plus autant d’influence et on se rapproche d’un bobinage sur air (avec, en plus, les pertes dans le noyau). Un bobinage a une fréquence de résonance propre grâce ou à cause de la capacité répartie entre spires qui constitue le condensateur du circuit oscillant. C’est ainsi que, alors que le tore fonctionne toujours parfaitement, on voit le TOS grimper sur une plage de fréquence puis rediminuer.
La seule solution est de séparer un peu les spires et d’utiliser un isolant ayant un diélectrique faible. En d’autres termes, il vaut mieux du fil émaillé que du fil isolé PVC ou téflon et
éviter un trop grand nombre de spires.

La courbe de réponse est aussi influencée par les pertes : comme il y a échauffement, il y a une forme de résistance et celle ­ci vient en parallèle sur l’impédance vue par le balun.
C’est comme si le rapport de transformation était plus faible. Mais cela a un effet pervers. Exemple : si votre antenne a une impédance 10% trop élevée (donc un ROS de 1,1) et votre tore a 10% de pertes (soit 1,1 de ROS aussi, mais dans l’autre sens), les TOS peuvent s’annuler (ou, du moins, se réduire) et vous avez 1:1 ; ce qui est loin d’être idéal comme le laisserait penser la mesure ! C’est ce qui se passe parfois avec des ununs sur T200­2 sur les bandes basses.

Nous parlions tout à l’heure de l’impédance faible de certains baluns sur les bandes basses. La réactance (= l’impédance du bobinage) vient en parallèle sur la charge et diminue celle ­ci. Il y a physiquement une self non négligeable entre la base de votre antenne et la terre alors que ce devrait être une self de choc. C’est pour cela, qu’on conseille une réactance égale à 10 fois l’impédance de charge. Mais c’est en vertu de ce phénomène que certains fabricants pouvaient affirmer que leur magnetic balun avait un rapport de transformation qui s’adapte à la fréquence.

Les tores de récupération

Nous en trouvons à profusion dans de nombreux appareils et beaucoup sont de belle dimension. Mais la taille n’a pas grand’chose à voir, c’est la section du tore qui détermine la puissance qu’ils peuvent supporter :

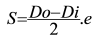
Avec :
S = la section du tore
Do : diamètre extérieur
Di = diamètre intérieur
e : épaisseur du tore
Vous pouvez donc avoir un tore plus petit mais qui admet une puissance plus élevée. Et si vous empilez plusieurs tores identiques, la puissance admissible sera proportionnelle à ce nombre et l’élévation de température sera répartie entre les tores.
Exemple : vous disposez d’un tore qui admet 100W. Vous en mettez un second et l’ensemble admettra 200W. Puis 300W pour trois, etc.
Si l’élévation de température est de 120° (très plausible) deux tores atteindront 60° et trois ne chaufferont que jusque 40°. Tout cela simplement parce que la section utilisable est plus importante et l’énergie se répartit entre eux. Et, en prime, il faudra moins de spires mais cela peut être un inconvénient au point de vue puissance admissible.

Pour déterminer la perméabilité, vous bobinez 10 spires d’un fil quelconque que vous répartirez sur la circonférence du tore et vous en mesurez l’inductance. MiniRK possède une fonction pour déterminer les caractéristiques d’un tore inconnu. La perméabilité que vous obtiendrez sera celle disponible à vide. La température, la tension et le courant (même continu) influent sur celle­ ci dans de grandes proportions. Mais c’est souvent en mieux !

La valeur idéale pour le trafic en décamétrique se situe entre 100 et 300 mais peut aller jusque 1000 tout en donnant des résultats très acceptables. Seulement, un tore grade 61 chez Amidon ou C65 chez Ferroxcube vous donnera le moins de pertes et le meilleur rendement en large bande.

Les tores peints sont souvent en poudre de fer. On les détecte en donnant un petit coup de lime. Si elle glisse, ce sera de la ferrite. Si elle mord, c’est de la poudre de fer.
Attention : on trouve très souvent des tores peints et tendres (ou encapsulés dans deux coquilles en plastique) mais d’une perméabilité énorme (de 10.000 à 15.000 !). Ils sont, en fait, réalisés à l’aide d’un très mince ruban de fer doux enroulé sur lui ­même. Ces tores conviennent très bien pour la BF (pour reproduire les fameuses selfs de 88mH) mais absolument pas pour la HF !

Il y a des tores peints qui présentent une perméabilité de de >50 (types 26 ou 52 chez Amidon). Ils ne conviennent absolument pas pour réaliser un balun car ils absorbent une grande quantité d’énergie. Ils sont conçus pour le filtrage et, dans ce domaine, ils excellent. Ils sont souvent jaunes avec une face blanche (à ne pas confondre avec les Txx­6) pour le grade 26 et verts avec une face bleue pour le type 52.

Unun sur 2 piles de 3 tores en ferrite

µ = 800

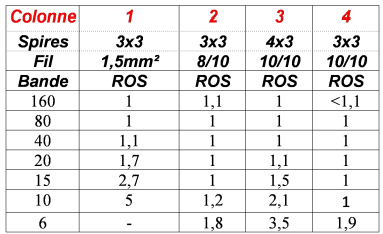
Le diamètre du fil a bien plus d’influence qu’on ne le pense généralement. Remarquez, colonne 1, l’entrée en résonance du bobinage.
Les tores tout verts sont différents et d’un autre fabricant.
Vous en dénicherez dans le filtrage basse tension des alimentations à découpage des PC. Ce sont souvent des T80 à T130 (ce nombre étant le diamètre en centième de pouce).
Passez-­y quatre spires au moins d’un fil d’alimentation ou d’un coaxial pour réaliser un choke balun par exemple. Si vous en empilez plusieurs, l’effet sera (très) approximativement proportionnel au carré du nombre de tores empilés. Il est préférable de mettre deux fois trois tores côte à côte qu’une pile de 6 tores pour la bonne raison qu’il faudra moins de spires et, de là, moins de pertes de
rendement (il y aura moins de fil susceptible de rayonner la HF avant qu’elle ne soit arrêtée). Cela est valable dans tous les cas.

On trouve aussi des tubes. Ils sont toujours en ferrite. Il y en a de deux types génériques : ceux à faible perméabilité (de 200 à 800) et de haute perméabilité (de 1000 à 3000). Les
premiers conviennent pour un balun, les seconds trouveront leur place dans un PA à transistor. A conserver donc. En application self de choc, ils ne conviennent vraiment qu’en VHF.

Les ferrites spéciales

Il y a des composants spéciaux qui fonctionnent très bien en applications HF comme les carcasses de transfo THT de TV ou moniteurs à CRT ainsi que les bobines de déflexions.
Leur perméabilité est souvent de 200 environ. Ne vous préoccupez pas de leur forme biscornue. Collez les éléments ensemble avec de la colle cyanolite (Super Glue). Cela fonctionne très bien et le très léger entrefer créé est même un peu bénéfique à la puissance supportée !
Cela est aussi valable pour un tore que vous avez cassé. Voilà une nouvelle qui va faire des heureux ou qui vont regretter de ne pas l’avoir su plus tôt…
Les carcasses E­-I ou similaires utilisés pour les transformateurs d’alimentation à découpage ne conviennent que pour les fréquences assez basses : de 20 à 200KHz.
Mais voyez les résultats d’une très faible partie des mesures que nous avons effectuées sur des baluns et ununs fonctionnels.

Le unun décrit ci­-contre tel qu’il a été conçu. Remarquez les fils de couleur. L’ordre est celui des couleurs standardisées en électronique et qui sont appliquées, notamment, aux
résistances. Le fil nu est la masse, le brun est le 1:1, le rouge est le 4:1 et l’orange est le 9:1. Pour la masse, comme c’est le fil du bobinage qui est employé pour la connexion, nous l’avons laissé nu.

Unun sur gros tube antiparasite en ferrite

Diam 28,5mm, long 28,5mm, µ = 650

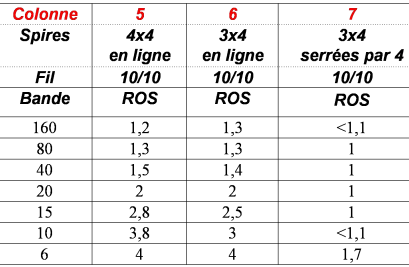  3x4 spires serrées par 4 : la meilleure configuration. P in : 188W sur 80m

Cadres ferrite de BCR PO­GO

µ = 125

1. barreau      10 sp = 9µH
2. barreaux   10 sp = 13µH
3. barreaux   12 sp = 22µH

Évolution de l’inductance.

2. barreaux : L multipliée par racine carrée de 2
3. barreaux : L multipliée par racine carrée de 3. Etc.

Ce gros tube est d’origine totalement inconnue ! Le fait est qu’il fonctionne très bien pour nos applications. Remarquez deux détails : les spires sont groupées par trois et sont volontairement légèrement espacées.

Ununs réalisés sur un fagot de trois barreaux de ferrite BCR ­

µ = 125

Le collage des trois barreaux. Il est conseillé de remplir les « V » entre les ferrites (photo ci­-contre) afin d’éviter qu’elles ne se brisent lors du bobinage du fil car elles ne sont jamais bien droites.

Unun sur 2 piles de 3 tores en ferrite

Les tores sont des anneaux en ferrite de+/­20mm de diamètre. On les trouve dans toutes sortes d’appareils, du côté de l’alimentation secteur. Elles servent d’antiparasite.
On y trouve un ou plusieurs fils enroulés environ 5 fois. Leur perméabilité est d’environ 600 mais peut monter à plus de deux fois cette valeur.
En général, elles correspondent plus ou moins à un Amidon FT82­43. Ce sont les plus courantes en récupération. Si vous y bobinez 10 spires, vous devez obtenir une inductance de 40µH environ. Si l’inductance est de plus de 50, elles ne conviennent pas car vous aurez trop de pertes sur les bandes hautes. Si elle est inférieure à 20, ce sera trop peu pour les bandes hautes. Vous pourrez néanmoins les utiliser à condition de mettre 40% de spires en plus, soit 5 ou 6 spires par enroulement.
Comme les anneaux sont grands, nous avons utilisé du fil d’installation électrique de 1,5mm² de section pour un premier essai comme le préconisent certains auteurs sur Internet.
Voyez la colonne 1.
Si nous le changeons pour du fil émaillé de 8/10, nous avons les résultats colonne 2. C’est nettement mieux ! Le PVC du fil électrique est donc à proscrire.
A la colonne 3, nous avons ajouté un quatrième enroulement pour obtenir du 16:1. Résultat acceptable sur une bonne partie du spectre décamétrique.
A la suite d’autres essais, il est apparu que le fait d’ajouter un quatrième enroulement était néfaste. Nous revenons donc à 3 enroulements en vrac et les uns à la suite des autres.
Miracle : nous obtenons des résultats très enviables colonne 4 ! C’est très rare dans le commerce où on publie rarement les courbes de TOS. Et pour cause… Remarquez, en passant, que le TOS est amélioré avec du fil de 10/10 au lieu de 8/10. Il est bien entendu que vous pouvez n’utiliser que deux enroulements pour faire un unun ou un balun 4:1. Pour réaliser un balun, le coaxial ira au début du premier enroulement et la masse (la tresse) au point de jonction des deux enroulements.
Un unun ou balun ainsi réalisé tiendra allégrement la puissance de nos transceivers. Vous pouvez ne mettre que 2 x 2 tores pour le QRP à condition d’ajouter une spire : 4 au
lieu de 3. Si vous en mettez 2 x 4, vous pourrez utiliser un petit linéaire sur 80m et un « gros » au dessus. Ainsi donc, lorsque vous en trouverez à très bon prix dans une caisse sur une brocante ou une foire OM, débarrassez­ en vite le vendeur !

Unun sur un gros tube en ferrite

Ces tubes sont aussi courants. En général, c’est un groupe de fil qui le traverse. De ce fait, la perméabilité est souvent élevée : de 1500 à 2500. Mais on en trouve qui ont une perméabilité de 500 à 800. Ceux-­là semblent fonctionner à merveille dans nos applications. Et nous avons eu la chance d’en trouver un particulièrement volumineux dans notre boîte ­à­ tores. Il mesure 28,5mm de diamètre extérieur, 15mm intérieur et 28,5mm de haut également.3 C’est donc du massif. Quatre spires donnent une impédance suffisante sur 80m.
Les colonnes 5 à 7 donnent les principaux résultats de nos tests ; car il y en a eu au moins une dizaine, tous plus décevant les uns que les autres. Jusqu’au moment…
Colonne 5 : 4 enroulements pour obtenir du 16:1. Le fil est réparti sur le pourtour du tube. Le résultat est mauvais.
Colonne 6 : on enlève simplement un enroulement. Là, ça devient très légèrement plus intéressant. Mais la différence est infiniment moins sensible que dans le unun précédent !
Ce qui marche pour deux piles de tores ne fonctionnent pas avec un tube ou un empilement simple de tores. Découverte à ne pas perdre de vue. On en revient donc à l’enroulement traditionnel des baluns et ununs : on bobine « trois fils en main ». Nous avons donc quatre spires de fils jointifs par trois. Et là, re-­miracle ! C’est encore mieux qu’avec notre unun à 2 x 6 tores ! Mais il ne
tiendra <que> 250 à 280W sur 80m (puissance calculée mais non vérifiée).

Ununs réalisés sur un fagot de trois barreaux de ferrite BCR

Un auteur anglais a réalisé un unun 9:1 à l’aide d’un barreau de ferrite récupéré sur un transistor défunt. Il a été reproduit à de nombreux exemplaires par les OMs. Vous avez probablement, vous aussi, une botte de ces antennes ­cadres dans vos tiroirs. Les expérimentations passées nous ont appris qu’un seul barreau était insuffisant pour supporter la puissance de nos TX. Deux sont de rigueur. Et tant qu’à faire, nous en mettrons trois.
Des mesures préalables nous montrent que le coefficient AL est défavorable : le flux n’est pas bouclé comme avec un tore. Il est en effet concentré dans le barreau mais doit faire le restant du chemin de retour « à pied » alors que, dans un tore, il est emprisonné dans l’anneau et peut se déployer à son aise. Il faudra donc nettement plus de spires. Nous en avons mis 13 (par enroulement) mais il en aurait fallu bien 15 !
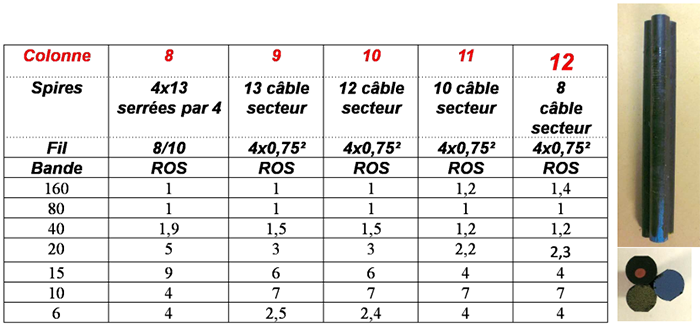
Colonne 8 : quatre enroulements de 13 spires serrées par 4 . Catastrophe : c’est juste bon pour le 160 et le 80m. Au-­delà, c’est inutilisable.
On essaye le système d’un OM anglais : un câble secteur à quatre conducteurs. Nous commençons par 13 spires et nous diminuons jusque 8 spires. 8 et 10 spires, c’est ce que cet auteur préconise. Vous pouvez en voir les résultats colonnes 9 à 12. No comment, les chiffres parlent d’eux­-mêmes.
Vous aurez remarqué que, après être monté assez haut, le TOS baisse à mesure que la fréquence augmente. C’est probablement dû à un phénomène de résonance naturelle des enroulements. Ceux-­ci forment, avec les capacités réparties entre spires, un circuit accordé. En effet, plus on « monte en fréquence », moins la ferrite est active. Et comme ici, il y a beaucoup de spires (39 spires) et que les fils sont proches les uns des autres, les capacités parasites ne sont plus négligeables.

Et pour terminer…

Les photos d’un petit balun 4:1 tout mignon, qui tient dans le creux de la main, mais redoutable ! En effet, ses performances sont comparables à celles des ununs qui ont été décrits dans cet article et il « tient » ses 100W, même sur 80m si le TOS n’est pas trop élevé.

Conclusion

Nous avons, à notre disposition, des composants précieux avec lesquels nous réaliserons des baluns et des ununs qui pourront rivaliser sans honte avec les meilleures réalisations commerciales vendues à prix d’or. Notez bien les remarques et les observations faites et voyez si elles ne sont pas applicables à des produits commerciaux.
Le unun 9:1 est valable mais pas n’importe comment et avec n’importe quoi. Une différence de 2, voir 3 points au S-­mètre entre un bon unun et de la camelote n’est pas si rare que cela. Le Magnetic Balun originel est réalisé comme à la colonne 6 mais avec beaucoup plus de spires et un enroulement externe de couplage. Là est sans doute la raison pour laquelle ses concepteurs pouvaient dire que le MLB « s’adaptait à la fréquence de travail ». Pour info : il était déconseillé de lui appliquer plus de …2W.
CQFD

Article paru dans le QSP N°30 de mars 2013

A propos de l'auteur

Guy Marchal

Administrateur-délégué chez Centre Multimédia Don Bosco a s b l. Il écrit de nombreux articles dans le CQ-QSO belge. Président du radio-club de Namur.

See author's posts