Faisant suite à un article qui expliquait la fabrication de trappes coaxiales construire son dipôle pour le 30m 40m et 80 m, j'ai voulu approfondir le problème des trappes. En parcourant d' anciennes revues ON5VL j'ai vu que l'on en avait déjà parlé. José ROBAT, ON7TP avait traduit un article de Robert C.SOMMER, N4UU.
Cet article est d'un accès facile et très bien expliqué c'est pourquoi en guise d'explication je vous le repropose.
Les trappes d’antenne à haute réactance effective donnent une bonne performance et une largeur de bande effective accrue.
L’auteur donne des informations détaillées pour les trappes à câbles coaxial de même que des courbes pour les deux types de câbles
Ci-contre quelques exemples de trappes construites avec du câble coaxial vue de mon ancien article
La conception habile d'utiliser la même longueur de câble coaxial pour former le bobinage et le condensateur d'une trappe d'antenne à résonance parallèle apparut pour la première fois dans une publication radio-amateur en 1981.
On s'est aperçu que les trappes à câble coaxial étaient à large bande, bon marché, facile à construire, stables par rapport aux variations de la température et capables de fonctionner à des hauts niveaux de puissance assez surprenants. En outre, ces trappes peuvent être de petite taille et légères.
Cet article montre un diamètre optimum pour une telle trappe, permettant l'obtention d'une fréquence de résonance spécifique en n'utilisant qu'une longueur minime de câble. En minimisant la longueur du câble, non seulement on en réduit le coût, le poids et les pertes associées au câble, mais on atteint le maximum de largeur de bande sur laquelle l'impédance à résonance parallèle demeure haute. Les données de construction de ces trappes, pour chacune des bandes HF, sont données dans les figures (1).
Un peu de mathématique :
La figure 1 montre la coupe d'une trappe à câble coaxial. Supposons que l'épaisseur du câble (diamètre extérieur) est de « t » en pouce, et que le câble est enroulé sur un support cylindrique dont le diamètre extérieur est de « d » en pouce, de façon à nous donner un bobinage de « n » spires. Assumons que le bobinage est à spires jointives, obtenant ainsi la plus grande inductance pour un nombre de spires donné. Assumons également qu'un demi pouce de câble blindé est utilisé à chaque bout du bobinage, en « queue de cochon » pour entrer dans le support du bobinage. La longueur totale du câble blindé sous de telles conditions s'approche de très près de πn (d +t) + 1 pouce (2,54 cm). Si la capacité distribuée du câble est de Co pF par pied (30,48 cm), la capacité totale du câble est égale à dans l'équation 1 :
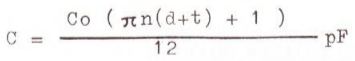(équation 1)
En utilisant la formule standard pour inductance, l'inductance du bobinage formé par le câble coaxial peut être exprimé comme ceci dans l'équation 2 :
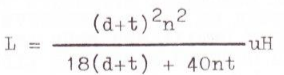(équation 2)
Vu que le diamètre moyen du bobinage est d+t et la longueur du bobinage à spires jointives est nt. Lorsque l'âme du câble, d'un côté est connectée à la masse de l'autre côté du câble, comme on peut voir sur la figure 1, nous sommes en présence d'un circuit à résonance parallèle. La fréquence de résonance est donnée par la formule connue dans l'équation 3 :
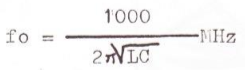(équation 3)
L étant exprimé en microhenry et C en picofarad. Pour tout jeu sélectionné de paramètres de trappes (d, t, n et Co) on utilise les équations 1 et 2 pour déterminer C et L respectivement, et l'équation 3 donne, avec précision, la fréquence de résonance.
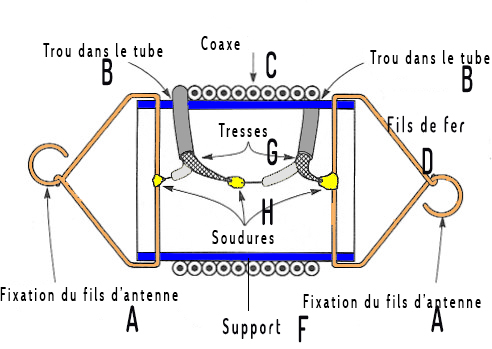
Figure 1 : vue en courbe d’une trappe construite avec du câble coaxial sur un support en PVC
Explication de la figure 1 ci-dessus :
- A : Attaches pour le fil d'antenne (à souder)
- B : Trous dans le tube PVC
- C : Spires avec le câble coaxial
- D : Fil de fer rigide
- E : Même que A
- F : Support du bobinage
- G : Tresse (masse) du câble coaxial
- H : Soudures
Paramètre d’une trappe optimum :
Comme décrit ci-dessus, il est facile de déterminer fo dès que l'on a sélectionné les paramètres de la trappe. En pratique, on choisit une valeur de fo et ensuite on détermine les paramètres de façon à obtenir la valeur sélectionnée de fo.
Ceci s'obtient en plaçant les données correctes des équations 1 et 2 dans l'équation 3 pour accomplir quelques manipulations algébriques pour arriver à l'équation cubique :
A3n³ + a2n² + a1n + a0 (équation 4)
Où : a0 = -216.000.000 (d+t)
a1 = -480.000.000 t
a2 = (2πfo)² (d+t)² Co
a3 = π (2πfo)² (d+t)³ Co
Donc, on sélectionne les paramètres d, t, fo et Co, on calcule les coefficients a0, a1, a2 et a3 et ensuite on résout l'équation 4 pour trouver la valeur propre de n. Dès que n est déterminée, la longueur totale du câble coaxial peut être calculée à partir de la formule :
L = π n(d+t) + 1 pouce (équation 5)
En utilisant, par exemple, du câble RG-174/U et 14,174 MHz comme fréquence fo, les équations 4 et 5 étaient évaluées pour différentes valeurs de d et t, et les résultats donnant la longueur « L » requise du câble en fonction du diamètre extérieur du support d sont montrées en figure 2.
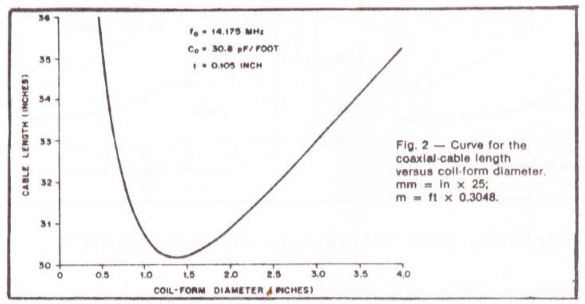
Figure 2 : Courbe du câble coaxial par rapport au diamètre du support du bobinage. (inches = 2,54 cm)
Sur cette figure 2, la longueur du câble est inscrite verticalement et le diamètre du support de la bobine est inscrit horizontalement. Toutes les mesures sont données en pouces (inches).
Il est intéressant de noter qu'une longueur minimum de câble permet d'atteindre la résonance à une fréquence de résonance sélectionnée. Par conséquent, la figure 2 montre qu’une trappe résonante dans la bande des 20 mètres faite avec du coaxial RG174/U sera optimum si ce câble est enroulé sur un support d'un diamètre de 1,4 pouce. (3,556 cm)
Courbes :
Les équations 4 et 5 furent utilisées pour pouvoir établir les courbes montrées en figure 3 (de A à D) lorsqu'on se sert de câble coaxial RG174/U et les courbes de la figure 4, lorsqu'on utilise du câble coaxial RG58/U.
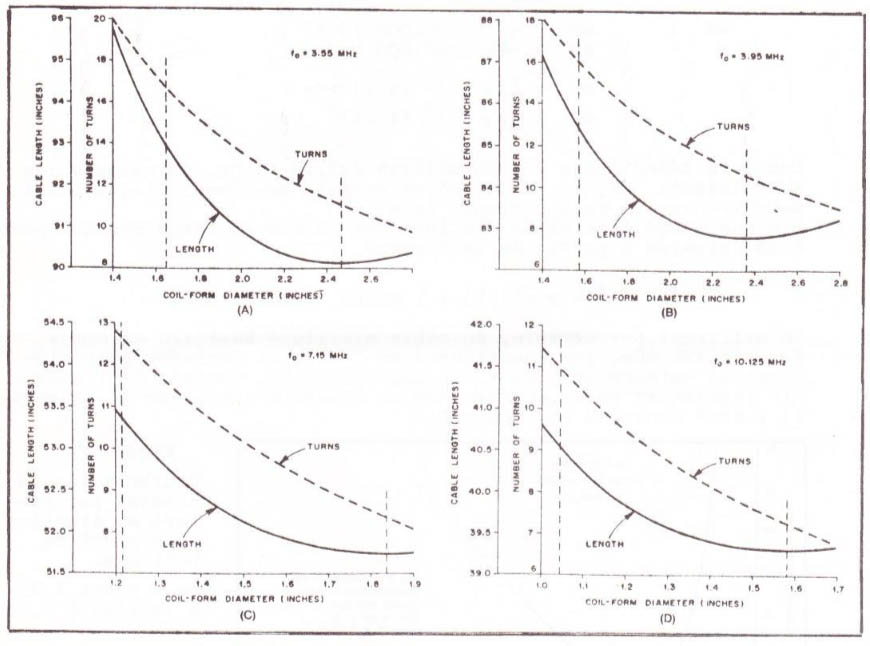
Figure 3 : Courbes établies pour utilisation du câble RG174/U.
Les paramètres nominaux de câble utilisés pour ces calculs sont :
RG174/U : t = 0,105 pouces (2,667 mm) | Co = 30,8 pF/pied (par 30,48 cm)
RG58/U : t = 0,200 pouces (5,08mm) | Co = 28,5 pF/pied (par 30,48 cm)
Chaque carte de courbe montre la longueur du câble et le nombre de spires requis pour la résonance dans une des bandes HF amateur à travers une échelle étroite de diamètres du support du bobinage. La ligne verticale (en pointillé) se trouvant à droite indique la valeur précise de « d » qui minimise « L ». Ce point peut être trouvé en utilisant différents calculs et en ressoudant une équation de cinquième ordre.
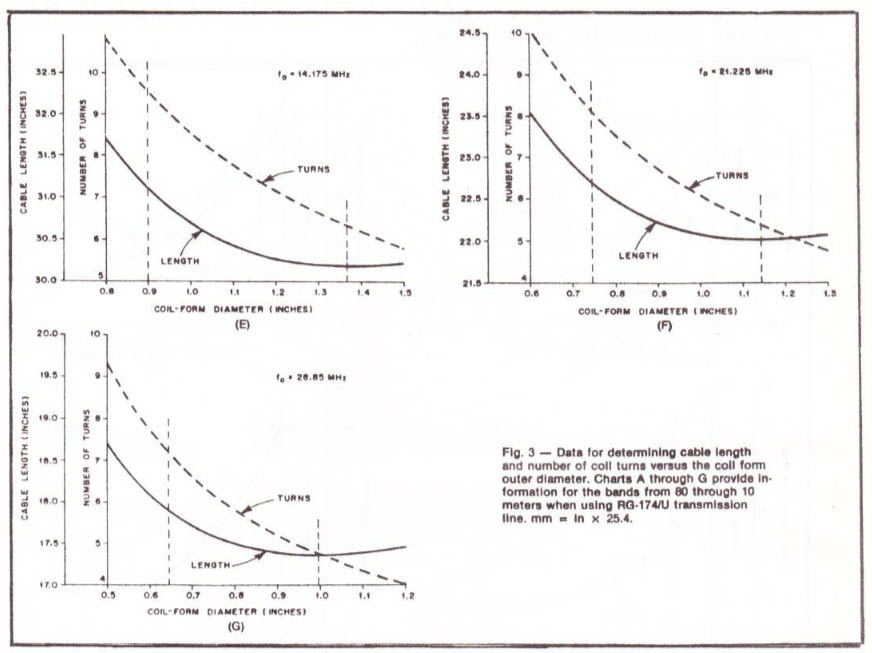
Figure 4 : (de E à G). Comme la figure 3 (A à D), ces courbes déterminent la longueur du câble et le nombre de spires par rapport au diamètre extérieur du support du bobinage.
Lorsque l'on utilise du câble coaxial RG174/U cela donne dans les figures 3 et 4 : A et B pour le 80 m | E pour le 20 m | C pour le 40 m | D pour le 30 m | F pour le 15 m | G pour le 10 m, lorsqu'on utilise du câble coaxial RG174/U.
Les résultats montrent qu'une trappe à câble coaxial optimale est caractérisée par une configuration de bobinage dans laquelle la longueur du bobinage « nt » est égale à 0,450 fois le diamètre principal du bobinage « d+t ».
De ce fait, les deux termes dans le dénominateur de l'équation 2 sont égaux. La ligne verticale (en pointillé) à gauche indique cette valeur « d » qui donne source à une configuration carrée de la bobine, dans laquelle la longueur (L) et le diamètre (d) de la bobine sont égaux.
En général, des bobinages carrés ont un « Q » assez élevé (Q= coefficient de surtension). Il n'est probablement pas prudent de choisir un diamètre inférieur à celui de la configuration du bobinage. Pour obtenir le maximum de performance de la trappe, le diamètre du support du bobinage doit être tel que la longueur du câble est minimisée. Étant donné que cela n'est pas toujours possible du fait que la mesure propre du matériel utilisé n'est pas toujours disponible, il faudra se servir d'un diamètre plus petit, mais un diamètre plus grand que celui qui donné source à un bobinage. En tous cas, l'échelle des diamètres entre les configurations optimum est assez vaste pour qu'on puisse trouver le matériel nécessaire.
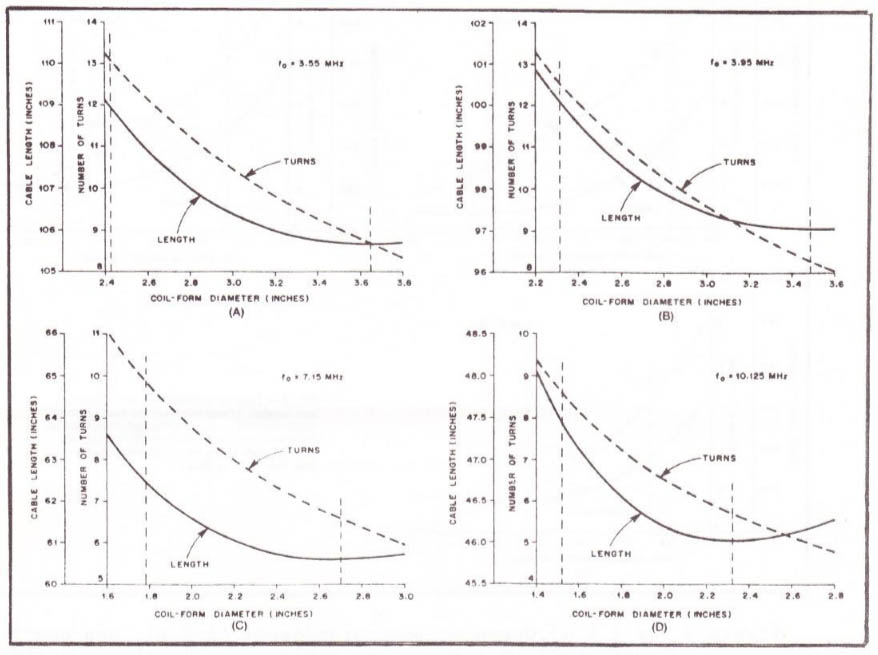
Figure 5 (A à D) : mêmes courbes qu’en figure 3 mais en utilisant du câble coaxial RG58/U
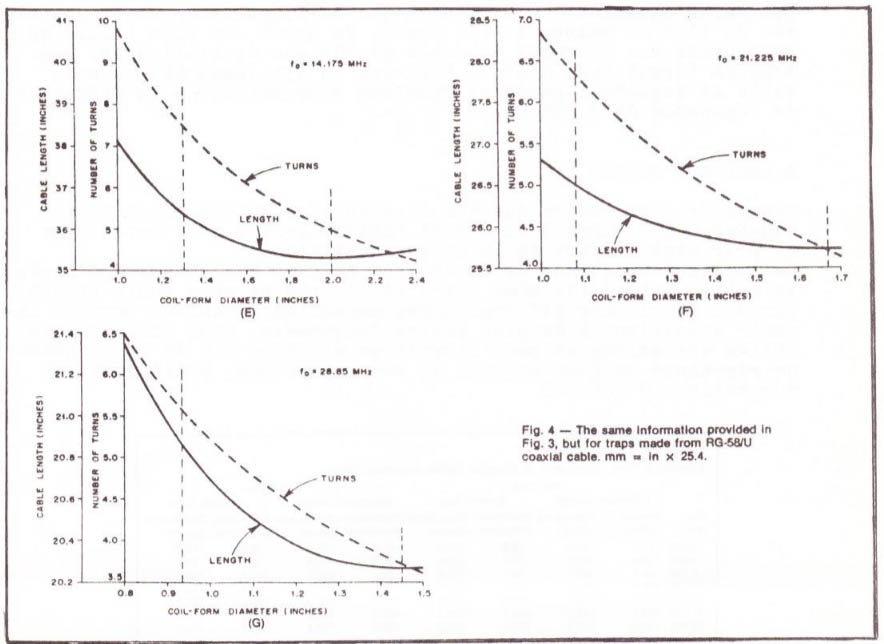
Figure 6 (E à G) Mêmes courbes qu'en figure 4 mais en utilisant du câble coaxial RG58/U
Exemples de construction :
► Supposons la construction d'une trappe pour le 15 mètres avec du câble coaxial RG174/U.
D'après la ligne verticale (en pointillé) de la figure 3F on voit que le support du bobinage doit être plus grand que 0,75 pouce (1,905 cm), un diamètre de 1,14 pouce (2.54 cm) étant optimum. On peut trouver chez le marchand des tubes en PVC de 3/4 de pouce ayant un diamètre extérieur de 1,10 pouce (2,794 cm) (près du diamètre optimum).
La figure 3F montre qu'en utilisant un diamètre de 1,10 pouce (2,795 cm), la trappe nécessite une longueur de 22 pouces (55,88 cm) de câble, bobiné en une self de 5 spires et demi.
► Comme deuxième exemple, supposons une trappe pour le 20 mètres, faite avec du coaxial RG58/U. D'après la ligne verticale (en pointillé) de la figure 6E, le diamètre du support de la bobine doit être supérieure à 1,3 pouce (3,302 cm), le diamètre optimum étant de 2 pouces (5,08 cm).
En ce cas, on utilisera un morceau de tuyau PVC de 1-1/4 pouces (3,175cm) dont le diamètre extérieur sera de 1,66 pouces (4,2164 cm). La figure 6E montre que cette trappe nécessite une longueur de câble de 35-1/2 pouces (90,17 cm) bobinée en 5-3/4 spires.
► Comme exemple final, voyons le projet d'une trappe pour le 80 mètres à construire avec du câble coaxial RG174/U, et, résonant sur 3.550 MHz. Pour une pour une fo = 3.55 MHz voyons les courbes de la figure 3A. Il est clair que le diamètre le plus approprié pour le support du bobinage pour la partie inférieure de la bande est de plus ou moins 2,47 pouces (6,2738 cm). En ce cas, un tube en PVC, ayant un diamètre extérieur de 2,25 pouces (5,715 cm) peut être utilisé pour construire une paire de trappes à mettre sur une antenne en « V inversée » par exemple. Il faut 12 spires pour une résonance sur 3.55 MHz. L'équation 5 nous montre que la longueur requise du câble est de plus ou moins 84 -1/4 pouces (213,995 cm). Vu qu'il est plus facile de raccourcir une longueur de câble plutôt que de l'allonger, ces trappes doivent tout d'abord être bobinées en utilisant 86 pouces (218,44 cm) de câble et ensuite légèrement réduites pour arriver à la fréquence de résonance de 3.55 MHz.
A propos d’accord :
Notre expérience montre que des trappes construites proches des données des figures 3 et 4 sont habituellement résonantes avec 1% d'écart de la fréquence voulue. De légères variations de « Co » et de « t » peuvent être observé d'après le câble utilisé et d'après ce même câble produit par des fabricants différents. Des capacités parasites peuvent devenir signifiant à de plus hautes fréquences. Pour compenser de telles variations et pour fournir un ajustage fin de la fréquence de résonance pour un segment de bande préférée, voici quelques suggestions d'accord avec 2 câbles coaxial différents
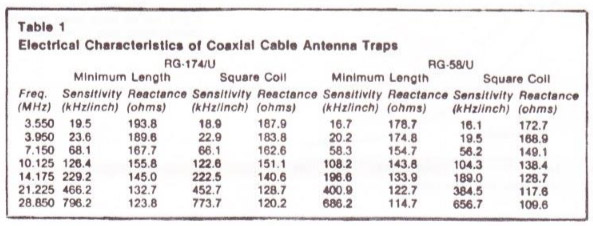
Tableau 1 : Caractéristiques électriques d’une trappe et d’un câble coaxial. (Minimum length = longueur minimum) (Square coil = bobinage).
Les valeurs de « L » et de « n » que l'on retrouve en figure 3 laissent une queue de cochon de 1/2 pouce (1,27 cm) de câble blindé à chaque extrémité du bobinage. Il faut donc commencer la trappe en laissant un supplément de 1 à 2 pouces (2.54/5,08 cm) pour les connexions. Si une longueur additionnelle de câble blindé est laissée à l'intérieur du support du bobinage, la capacité augmentera ; par conséquent, la fréquence de résonance diminuera. Cette sensibilité de la fréquence de résonance par rapport à la longueur du câble fut calculée et on la trouve dans le tableau 1 ci-dessus, en réduction d'unités de kilohertz en fo par pouce de câble coaxial additionnel.
Pour obtenir la résonance près de 7.050 MHz avec du RG174/U, par exemple, le tableau 1 qu'une longueur additionnelle d’un pouce de câble coaxial à l'intérieur du support de la bobine diminuera la fréquence « fo » de plus ou moins 66 à 68 kHz. Une longueur additionnelle de 1 -1/2 pouce fera chuter la fréquence « fo » de plus ou moins 100 kHz, donc la fo tombera de 7.150 MHz à 7.050 MHz.
[wp-svg-icons icon="thumbs-up" wrap="i"] Pour augmenter la fréquence de résonance, le câble coaxial à l'intérieur du support peut être redressé de façon à réduire la capacité, et pour réduire l'inductance, on peut écarter légèrement les spires sur le support.
Largeur de bande :
La largeur de bande utilisable de la trappe est la partie sur laquelle l'impédance de résonance parallèle reste assez élevée pour isoler ou pour « piéger » les sections extrêmes de l'antenne. Faisant abstraction des pertes, il peut être aisément démontré que l'impédance d'un circuit à résonance parallèle peut être exprimé comme suit dans l'équation 6 :
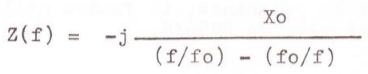
Où Xo est la réactance de chaque élément (C et L) à la fréquence de résonance « fo » et « f » étant la fréquence de travail. On remarquera que Z(f) est proportionnel à Xo.
Par conséquent, un Xo de grande valeur donnera une largeur de bande opérationnelle relativement grande. La longueur minimum du câble équivaut à Xo maximum. Les valeurs de réactance montrées dans le tableau 1 sont les valeurs de Xo pour des trappes à câble coaxial. Basé sur ces données, les trappes faites avec du RG174/U possèdent une largeur de bande opérationnelle légèrement plus grande que les trappes faites avec du RG58/U. Dans les deux cas ces trappes auront la largeur de bande opérationnelle la plus grande.
Techniques de construction :
Tableau 2 : caractéristiques de quelques trappes utilisant du câble coaxial RG174/U
La technique de construction décrite par CARTER (illustré en figure 1) donne des trappes poids—plume si construites avec du câble coaxial RG174/U .
En début de cet article on peut voir une « famille » construite par l'auteur, pour être utilisée avec des dipôles. Leurs caractéristiques sont données dans le tableau 2 ci-contre donnant colonne par colonne la bande de résonance, le diamètre (en pouce) du support du bobinage, le nombre de spires, le poids total (en once (1 oz=28,35 gr). Des configurations alternatives pour des trappes pour dipôles furent décrites par DeMaw et Johns, lesquels considèrent également la construction de trappes à câble coaxial pour des antennes verticales et des beams. En tous les cas, on peut appliquer les données et les courbes de cet article-ci.
Puissance :
Les trappes à câble coaxial peuvent travailler avec des niveaux de puissance (alimentation) assez élevées. Une antenne en « V inversée » pour les 40/80/160 mètres fut construites avec du RG174/U, donc, des trappes miniatures comme décrites dans cet article. Aucun problème en 40 et en 80 mètres avec une puissance d'entrée d'environ 1 kW. En travaillant sur le 160 mètres en CW avec une puissance de sortie de 1 ,4 kW, une des trappes du 80 mètres fut totalement anéantie.
Ceci était due au surchauffe excessive, causant un court-circuit interne entre l'âme et la masse du câble coaxial. Les autres trappes montrèrent des signes de surchauffe mais maintenaient leur intégrité électrique. D'après cette expérience, il apparait que des trappes miniatures à câble coaxial, faites avec du RG174/U, peuvent être utilisées en toute sécurité si la puissance moyenne vers l'antenne n'excède pas 500 W. Pour de plus hauts niveaux de puissance, il faudra utiliser des trappes plus grandes faites avec du RG58/U.
Reconnaissance :
Je tiens à remercier Mr.Nicholas Perriello, qui produisit le dessin de la figure 1 ; Mr.Steven Van Weddingen, qui fit pas mal de calculs sur sa calculatrice programmable (?) ; Dr.F.A. Burkle-Young, qui donna un coup de main pour les calculs et fit le manuscrit et, Ms.Diane Weeks qui prépara le texte dactylographié.
Références :
(1) R.H.Johns "Coaxial Cable Antenna Traps". QST MAY 1981
D. DEMAW "Lightweight Trap Antennas-Some Thoughts"QST JUNE 83 )
E.D. Carter "Small Yightweight traps for a 40/80 dipole" Potmoac Valley Radio Club News letter.
The ARRL Handbook for the Radio Amateur, 62nd edition
Conversion mesures : 1 pouce = 25,4 mm ; 1 pied = 0.3048 mètres
Traduction française José ROBAT ON7TP pour ON5VL de juin 1985.
A propos de l'auteur
