Analyseur de spectre et radioamateurs

L’analyseur de spectre chez les radioamateurs est un des appareils de mesure radiofréquence par excellence.  Il s’agit probablement de l’instrument de mesure le plus prisé après le multimètre électronique,l’oscilloscope et le générateur de signaux.  L’analyseur de spectre est longtemps resté le privilège des ingénieurs en électronique et en radiocommunications mais le monde évolue et heureusement les radioamateurs se sont mis à la page

Ainsi, nous pouvons actuellement disposer d’un tel appareil à un prix OM, par exemple sous la forme d’un module compact qui se raccorde sur un ordinateur portable par l’intermédiaire d’un port de communication USB (Universal Serial Bus).  En outre, il n’est plus rare de nos jours en 2016 d’avoir une prise de contact directe avec l’analyse spectrale des fréquences grâce à la présence d’afficheurs spécifiques sur les émetteurs–récepteurs modernes à l’usage des radioamateurs, ou grâce à des logiciels particuliers et dédiés.

Fig. 1 : Clichés extraits du bandeau d’accueil du site Internet radioamateur ON5VL (2015) illustrant des afficheurs de spectre de fréquence.

À l’heure de l’informatique, qu’en est-il des analyseurs de spectre de laboratoire ?

L’analyseur de spectre radiofréquence reste une des pièces maîtresses des laboratoires professionnels de radiocommunications et est utilisé la plupart du temps dans la recherche d’ingénierie ou pour effectuer des mesures de précision.  L’analyseur de spectre se révèle utile entre autres dans le domaine des transmissions à modulations numériques modernes telles que GSM (Global System for Mobile Communications), réseaux sans fil Wi-Fi (marque de la Wi-Fi Alliance du consortium Wireless Ethernet Compatibility Alliance WECA), 256QAM (Quadrature Amplitude Modulation, symboles représentés par 8 bits), etc.  Les appareils qui équipent de tels laboratoires sont en général du dernier cri des grands constructeurs (comme par exemple les analyseurs de spectre temps réel) et de tels instruments aussi performants sont actuellement inabordables pour les radioamateurs.

Toutefois, les analyseurs de spectre de laboratoire issus du marché de seconde main deviennent de plus en plus abordables pour les radioamateurs.  Certes, ceux-ci sont parfois assez sportifs à utiliser, mais cela peut nous offrir le défi d’apprendre et de maîtriser le contenu d’un des chapitres du programme de l’examen de la licence HAREC (Harmonized Amateur Radio Examination Certificat) avant d’utiliser un analyseur de spectre.  En effet, il vaut mieux apprendre un peu de théorie et de technique avant d’utiliser un appareil de mesure plutôt que faire le contraire et « mettre la charrue avant les bœufs ».

Fig. 2 : Analyseur de spectre et Radioamateur. Illustration d’un émetteur–récepteur FT-736R sous test avec un analyseur de spectre HP 8563E et un générateur à deux canaux HP 3326A.  Les relevés des mesures sont archivés sur un ordinateur portable par l’intermédiaire d’une interface GPIB-USB Prologix (GPIB : General Purpose Interface Bus). L’émetteur sous test est raccordé à l’analyseur de spectre par l’intermédiaire d’un atténuateur de puissance Bird 500-WA-FFN-30 (500 W 30dB) suivi d’un atténuateur Narda 766-20 (20 W 20 dB) tous deux situés en haut à droite de la photo.  Un DC-Block-limiteur Agilent N9355B (+10 dBm) est placé immédiatement à l’entrée de l’analyseur de spectre afin de protéger l’entrée HF de toute fausse manœuvre (Better safe than sorry ! Il vaut mieux prévenir que guérir).

Le but de cet article est de faire un tour d’horizon de ce qu’est un analyseur de spectre afin d’appréhender l’utilisation d’un tel appareil et de montrer de manière ludique les types de mesure que l’on peut effectuer avec cet instrument.  Nous utiliserons bon nombre de termes en anglais mais ceux-ci seront tous chaque fois définis en français.
Nous invitons le lecteur à se documenter pour approfondir le sujet, par exemple avec la série des notes d’application Hewlett-Packard AN150, AN150-1…AN150-15, les publications Rohde & Schwarz, Anritsu, Tektronix, etc...

Qu’est-ce que l’analyse spectrale ?

Intuitivement, dans la vie courante, nous effectuons quotidiennement de l’analyse spectrale, c’est-à-dire l’analyse d’un signal dans le domaine de la fréquence.  Reconnaître le timbre d’un instrument de musique ou identifier une voix humaine, distinguer la couleur d’un feu de signalisation routière au vert ou au rouge, c’est de l’analyse spectrale.  En effet, un signal simple ou complexe peut être décomposé en une série de composantes de différentes fréquences, de différentes amplitudes et de phases relatives entre elles.  Nous devons cette découverte au mathématicien Jean-Baptiste Joseph Fourier né au XVIIIème siècle ayant donné son nom aux séries de Fourier, à l’analyse et à la transformation de Fourier.  L’essentiel de cette découverte est que tout signal peut être décomposé en une somme d’un fondamental et d’harmoniques.

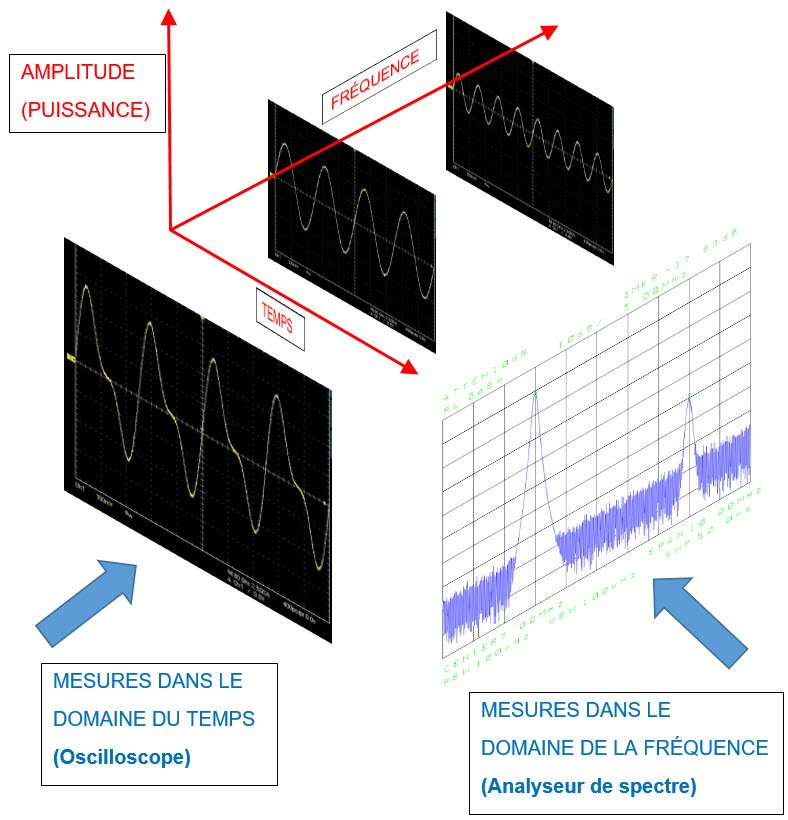
Fig. 3 : Analyse d’un signal : soit dans le domaine du temps soit dans le domaine de la fréquence.

En quoi l’analyse spectrale peut-elle se révéler utile ?

Un signal variable peut être observé dans le domaine du temps et nous informer par exemple sur la forme d’onde de ce signal.  En revanche, un signal observé dans le domaine de la fréquence nous donnera bien plus d’informations sur les composantes qui forment ce signal.  En effet deux sinusoïdes différentes peuvent se ressembler à l’œil nu sur un oscilloscope mais l’une d’entre-elles peut révéler des harmoniques d’amplitudes non négligeables sur un analyseur de spectre.

Dans le domaine des radiofréquences, cela a toute son importance : émettre sur la fréquence porteuse d’un signal modulant est donc envoyer sur l’éther un rayonnement électromagnétique (porteur d’une information) qui est supposé être caractérisé par une fréquence bien connue, bien définie et cela à l’exclusion de toutes autres fréquences porteuses, en particulier de fréquences harmoniques.  La pureté spectrale d’une émission radio est une des caractéristiques essentielles afin d’éviter des brouillages d’émissions de tiers situées en dehors des bandes de fréquences allouées aux radioamateurs.  On n’arrête pas les ondes radio dans l’espace, même si celles-ci s’atténuent selon le carré de la distance.  Comme la perfection n’est pas de ce monde, l’enjeu est d’assurer à nos émissions radioamateur une pureté spectrale suffisante de façon à ce que l’amplitude des harmoniques soit réduite à un niveau acceptable défini par des normes qui sont rendues exécutoires par la législation en matière des radiocommunications.

Les harmoniques d’une fréquence porteuse ne sont qu’une partie émergente de l’iceberg en matière de radio-émissions.  Le signal radiofréquence émis ne se limite pas à une porteuse seule (sauf dans le cas des télécommunications en morse caractérisées par une onde entretenue continue pure, CW Continuous Wave) : l’information transmise sous forme de modulation de la fréquence porteuse a pour conséquence une complexification du signal porteur qui se traduit par l’occupation d’une portion de largeur de bande adjacente à la fréquence porteuse.  Le pilotage correct et efficace de la modulation doit contribuer à une maîtrise de la largeur de bande du signal émis.

Tout cela est vrai dans le meilleur des mondes, mais il subsiste dans la réalité des signaux parasites qui peuvent altérer la pureté spectrale d’une émission aux abords directs (ou non directs) de la porteuse et de la bande occupée par la modulation (la « largeur de bande nécessaire »).  Les signaux parasites sont répertoriés sous les appellations suivantes : « rayonnements non essentiels » (Spurious Emission), « rayonnements non désirés » et « émissions hors bande ».
Pour être bien comprises, ces appellations (ou dénominations) sont clairement définies dans les recommandations de l’UIT-R : ensemble des normes techniques internationales développées par le secteur radiocommunications de l’UIT (Union Internationale des Télécommunications), anciennement CCIR (Comité Consultatif International des Radiocommunications).

Voici ci-dessous ces définitions (extraits de : Recommandation UIT-R SM.329-9).  Ce texte peut apparaître rébarbatif mais il a un lien direct avec l’analyse spectrale.

Rayonnements non essentiels :

Rayonnement sur une ou sur des fréquences situées en dehors de la largeur de bande nécessaire et dont le niveau peut être réduit sans affecter la transmission de l'information correspondante. Ces rayonnements comprennent les rayonnements harmoniques, les rayonnements parasites, les produits d'intermodulation et de conversion de fréquence, à l'exclusion des émissions hors bande.

Rayonnements non désirés :

Ensemble des rayonnements non essentiels et des rayonnements provenant des émissions hors bande.

Émissions hors bande :

Émission sur une ou sur des fréquences situées immédiatement en dehors de la largeur de bande nécessaire, due au processus de la modulation, à l'exclusion des rayonnements non essentiels.

Largeur de bande nécessaire :

Pour une classe d'émission donnée, largeur de la bande de fréquences juste suffisante pour assurer la transmission de l'information à la vitesse et avec la qualité requises dans des conditions données.

Rayonnement harmonique :

Rayonnement non essentiel sur des fréquences qui sont des multiples entiers de la fréquence centrale.

Rayonnement parasite :

Rayonnement non essentiel produit accidentellement sur des fréquences indépendantes à la fois des fréquences porteuses ou caractéristiques d'une émission et des fréquences des oscillations résultant de la production de la fréquence porteuse ou caractéristique.

Produits d’intermodulation :

Les produits d'intermodulation non essentiels résultent de l'intermodulation entre :

• les oscillations sur les fréquences porteuses, ou caractéristiques ou harmoniques d'une émission, ou les oscillations résultant de la production de ces fréquences porteuses ou caractéristiques ; et
• des oscillations de même nature, d'une ou plusieurs autres émissions, en provenance du même ensemble émetteur ou d'émetteurs ou ensembles émetteurs différents.

Produits de conversion de fréquence :

Rayonnements non essentiels, ne comprenant pas les rayonnements harmoniques, sur les fréquences ou des multiples entiers de celles-ci, ou des sommes et différences de multiples de celles-ci, des oscillations utilisées pour produire la fréquence porteuse ou la fréquence caractéristique d'une émission.

Rayonnements à large bande et à bande étroite vis-à-vis de l’appareil de mesure :

Une émission à large bande est une émission « dont la largeur de bande est supérieure à celle des récepteurs ou d'un appareil de mesure donné » (voir Vocabulaire électrotechnique international (VEI)/Commission électrotechnique internationale (CEI), 161-06-11). Une émission à bande étroite est une émission « dont la largeur de bande est inférieure à celle des récepteurs ou d'un appareil de mesure donné » (voir VEI/CEI, 161-06-13).

Question - Que peut donc faire un analyseur de spectre dans tout cela ?

Réponse - voir et mesurer tout cela !  Et bien d’autres choses encore.

Sans être limitatif, voici encore quelques applications possibles avec un analyseur de spectre :

• Effectuer le relevé du bruit de phase d’un oscillateur ou d’un générateur (Phase Noise)
• Mesurer la puissance d’une émission dans un canal adjacent à celui que cette émission occupe
• Mesurer l’indice de modulation (ou déviation de fréquence) d’une porteuse modulée en fréquence
• Effectuer une surveillance (monitoring) du trafic radiofréquence sur une bande de fréquence
• Effectuer des mesures scalaires sur un circuit (mesures d’amplitude en fonction de la fréquence) avec un générateur suiveur à balayage (Tracking Generator) : courbe de réponse d’un filtre, d’un amplificateur, d’un étage mélangeur de fréquence, etc...
• Effectuer des mesures de distorsion harmonique
• Effectuer des mesures d’intermodulation (IMD)
• Démoduler un signal AM ou FM
• Effectuer des mesures sur une émission multiplexée (impulsions d’émission) d’un système TDMA (Time Division Multiple Access) en activant une fonction de déclenchement (Time Gating)
• Effectuer des mesures sur un signal d’une émission pulsée (modulation numérique tout ou rien) : mesure de la largeur d’impulsion et mesure de la répétition de cycle du train d’impulsions
• Effectuer des mesures d’interférences électromagnétiques (EMI)
• etc...

Qu’est-ce qu’un analyseur de spectre ?

Un analyseur de spectre est, en résumé, un super récepteur !  Un récepteur de mesure ?
Oui, il s'agit bien d’un récepteur superhétérodyne comme tous ceux que les radioamateurs utilisent pour la réception des radiocommunications. Toutefois, un analyseur de spectre a la faculté de balayer (avec une base de temps) une bande de fréquence en permanence (comme s'il s'agissait d'un scanner radiofréquence). Il a aussi la faculté de sélectionner à volonté une sélectivité désirée (résolution de bande passante de la fenêtre de réception, RBW : Resolution BandWidth). À la sortie du démodulateur (détecteur d'enveloppe), le signal démodulé n'est pas appliqué à un haut-parleur, mais bien à l'amplificateur de déflexion vertical d’un écran à tube cathodique par l'intermédiaire d'un amplificateur à réponse logarithmique pour obtenir une amplitude graduée en décibels. L’amplificateur horizontal de déflexion du tube cathodique est raccordé à la base de temps qui pilote le balayage en fréquence de l’analyseur de spectre. On obtient ainsi une mesure d’amplitude dans le domaine de la fréquence.

Comment réaliser un balayage en fréquence

Dans un récepteur superhétérodyne (à double ou à multiple changements de fréquences), le premier changement de fréquence s'effectue au moyen d'un mélangeur de fréquences piloté par un oscillateur local (hétérodyne). Il en est de même dans un analyseur de spectre. Le changement de fréquence s'effectue en général par battement supérieur : la fréquence de l'oscillateur local est supérieure à celle de la réception haute-fréquence désirée, avec un écart en fréquence qui correspond à celle de l’étage de la première moyenne fréquence (première fréquence intermédiaire).  C’est donc la fréquence de l'oscillateur local du premier changement de fréquence qui détermine la fréquence d'accord de réception. Cet oscillateur local est piloté par une tension de commande qui détermine sa fréquence d’oscillation : il s'agit d'un oscillateur commandé en tension (VCO : Voltage-Controlled Oscillator). Il suffit donc de piloter ce VCO par la rampe de tension de la base de temps de l'analyseur de spectre et on obtient ainsi le balayage en fréquence de celui-ci.

Comment sélectionner à volonté la sélectivité d’un super récepteur ?

La sélectivité d'un récepteur superhétérodyne tient principalement à celle des étages moyenne fréquence. Ainsi il suffit de placer une série de filtres passe-bande, dont on peut faire varier la largeur de bande passante, pour obtenir une sélectivité réglable à volonté dans l’analyseur de spectre.

Pourquoi est-il nécessaire de régler la sélectivité d’un super récepteur ?

Principalement pour pouvoir distinguer des signaux adjacents et proches en fréquence.  En très résumé, tout est une question de compromis entre l'étendue du balayage en fréquence de l’analyseur de spectre et la sélectivité appropriée pour cette étendue. Le compromis ne se limite pas à la sélectivité. En effet, le temps de transit (throughput) et le temps de montée (rise time) d'un signal à travers un filtre est fonction du nombre de pôles qui le constituent et, indirectement, de la bande passante de celui-ci. Ceci impose en corollaire une vitesse de balayage appropriée en fonction de la résolution de bande passante désirée (sélectivité désirée). Le temps de balayage conditionne indirectement la capacité en vitesse de mesure de l'appareil analyseur de spectre. Nous examinerons plus loin la raison et la nécessité du réglage de la résolution de bande passante d’un analyseur de spectre.

Un petit schéma vaut mieux qu'un long discours. Voici l'intérieur d’un analyseur de spectre en schéma bloc simplifié.

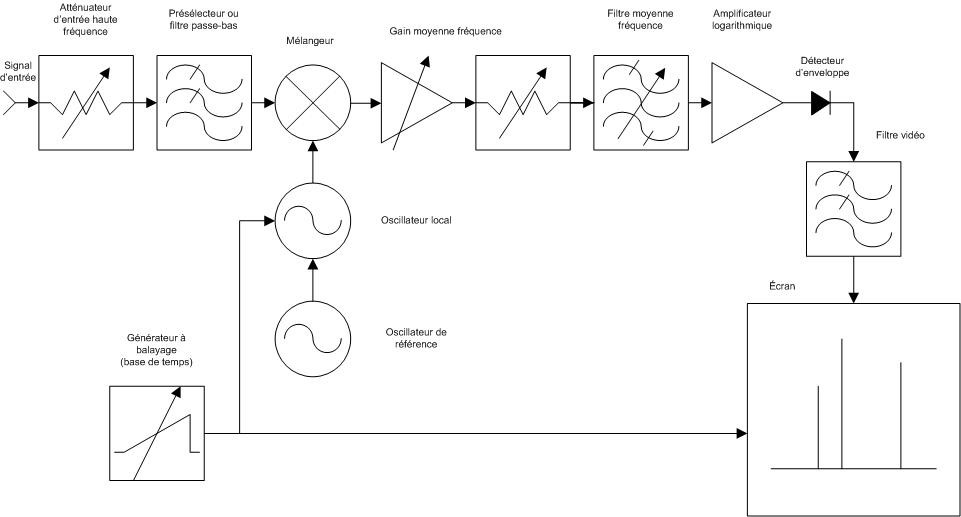
Figure 4 : Schéma bloc d'un analyseur de spectre du type hétérodyne et à balayage de fréquence. La chaîne des étages moyenne fréquence est représentée par un simple changement de fréquence. Dans la réalité, la chaîne moyenne fréquence comporte plusieurs changements de fréquence.

Nous supposons que le lecteur est déjà familiarisé avec le schéma bloc d’un récepteur superhétérodyne d’une station radioamateur.
Dans le schéma bloc ci-dessus, l’oscillateur local est piloté non seulement par la rampe de tension de la base de temps, mais aussi par un oscillateur de référence. L’oscillateur local fait partie en réalité d’une boucle d’asservissement de phase (PLL : Phase Locked Loop).  La fréquence du VCO est comparée à celle de l’oscillateur de référence pour assurer au VCO la précision et la stabilité en fréquence requise. L’oscillateur de référence est en général du type OCXO (Oven Controlled Xtal Oscillator) : oscillateur à quartz situé dans une enceinte chauffée et régulée en température (« four »).  Le VCO est en général du type YTO : YIG Tuned Oscillator ; YIG : Yttrium Iron Garnet, grenat d’yttrium et de fer (Y₃ Fe₅ O₁₂), oscillateur accordé par un résonateur YIG ; il s’agit d’une technologie toute particulière pour réaliser un VCO large bande et sur des fréquences très élevées (jusqu’à plusieurs dizaines de GigaHertz).
Nous avons décrit ci-dessus très sommairement un des types d’analyseur de spectre : analyseur hétérodyne et à accord de fréquence par balayage  (Swept Tuned Spectrum Analyzer). Les analyseurs de spectre temps réel sont basés sur un autre principe : l’analyse suivant la transformée de Fourier rapide (FFT : Fast Fourier Transform), mais cela est une autre histoire...

À quoi donc ressemble un analyseur de spectre ?

Cela ressemble à un « oscilloscope » car il y a un écran à tube cathodique ou un afficheur numérique à cristaux liquides (LCD) visible sur la face avant de l’appareil. En revanche à y voir de plus près, on y découvre une pléthore de boutons aux fonctions d’appellations étranges, c’est-à-dire peu habituelles à celles que l’on s’attend à rencontrer sur un oscilloscope.
Voici quelques photos d’analyseurs de spectre au cours de l’évolution de ce type d’instrument de mesure.  Nous avons choisi quelques modèles représentatifs du constructeur Hewlett Packard Agilent Keysight, mais aussi quelques autres modèles des constructeurs Advantest, Anritsu, IFR Aeroflex, Marconi Instruments, Rohde & Schwarz, Tektronix, etc...

Figure 5 : Le premier analyseur de spectre Hewlett Packard, HP851A/HP8551A en 1964 (Source Internet HP memory Project).

Très fort pour l’époque, en 1964 : un analyseur de spectre capable de mesurer des signaux jusqu’à 10 GHz ! (40 GHz avec mélangeur externe).

Figure 6 : Analyseur de spectre Hewlett Packard, HP141T (1968) (Photo de Dirk Ruffing - DH4YM).

Cet analyseur de spectre est relativement bien connu des radioamateurs. Ce modèle a équipé de nombreux laboratoires d’écoles techniques et universitaires. Sur le marché de seconde main, il n’est pas rare d’en trouver en 2016 à des prix compétitifs compris entre 250 et 1000 € avec tiroirs compris (IF + HF 110 MHz ou 18 GHz).

Figure 7 : Analyseur de spectre Hewlett Packard, HP 8558B HP181T (1973-1975) (Source Internet HP memory Project). Modèle très connu avec le HP 182T ayant aussi équipé de nombreux laboratoires d’écoles techniques et de petites entreprises en radiocommunications.

Figure 8 : Analyseur de spectre Hewlett Packard, HP8568A (1978) (Source Internet HP memory Project).

Figure 9 : Analyseur de spectre Tektronix, 494P (1983) (Source Internet Radau-Funktechnik).

Figure 10 : Analyseur de spectre Marconi Instruments, 2380/2383 (1986) (Source Internet Used Equipment Surplus & Storage Ltd).

Figure 11 : Analyseur de spectre IFR Aeroflex, A-7550 (1986) (Source Internet US Instrument Services).

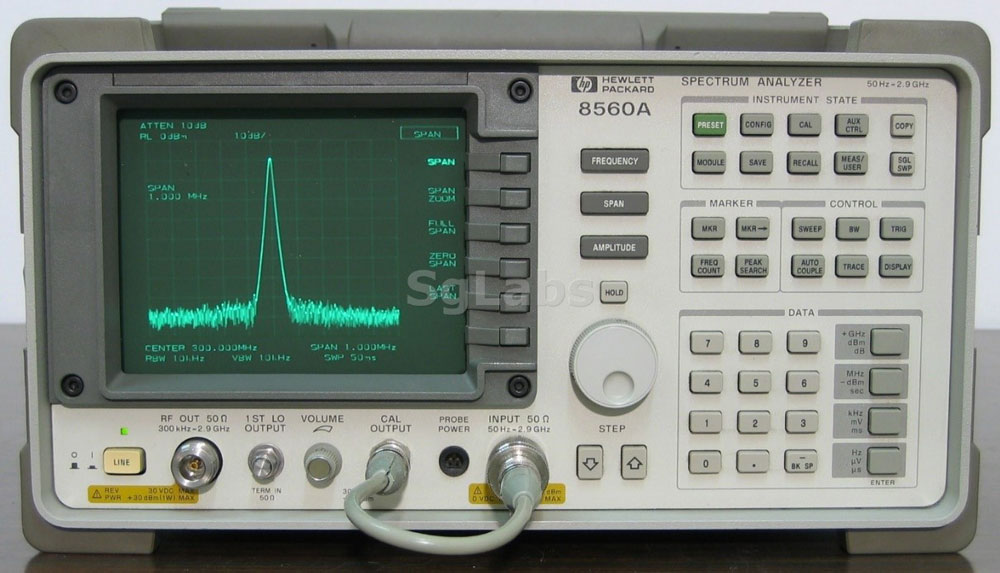
Figure 12 : Analyseur de spectre Hewlett Packard, HP8560A (1987) (Source Internet SG Labs).

Figure 13 : Analyseur de spectre Advantest R3272 (1995) (Source Internet Helmut Singer Elektronik, Feldchen Aachen).

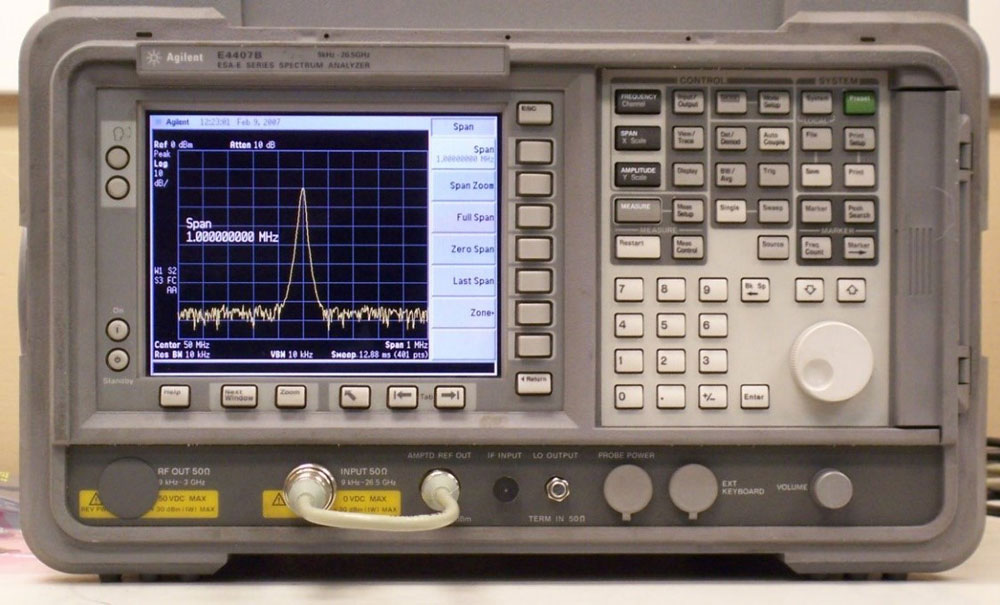
Figure 14 : Analyseur de spectre Agilent E4407B (2000) (Source Internet Cal Center Inc).

Figure 15 : Analyseur de spectre Anritsu MS2668C (2009) (Source Internet Helmut Singer Elektronik, Feldchen Aachen).

Figure 16 : Analyseur de spectre temps réel Tektronix RSA6114A (2009) (Source Internet EE Times).

Figure 17 : Analyseur de spectre temps réel Rohde & Schwarz FSVR (2010) (Source Internet R&S).

Figure 18 : Analyseur de spectre temps réel Agilent N9030A (2012) (Source Internet Microwave & RF).

Figure 19 : Analyseur de spectre portable Keysight N9344C (2011) (Source Internet Keysight).

Quelles sont les principales touches de fonction d’un analyseur de spectre ?

• FREQUENCY CENTER : réglage en fréquence au milieu de l’axe des abscisses du réticule de l’écran, en Hz, kHz, MHz ou GHz.
• FREQUENCY START, STOP : réglage en fréquence au début et en fin d’axe des abscisses du réticule de l’écran. Ces deux fréquences définissent automatiquement la portion de bande affichée à l’écran et donc l’étendue du balayage en fréquence de l’analyseur de spectre.
• SPAN : étalement du balayage en fréquence de l’analyseur, c’est-à-dire la portion de bande de fréquence affichée à l’écran entre le début et la fin du réticule, en Hz, kHz, MHz, ou GHz pour les dix divisions horizontales. On en déduit la largeur du balayage en fréquence en Hz, kHz, MHz ou GHz par division horizontale du réticule. La fonction Zero Span sera décrite plus loin.
• AMPLITUDE REFERENCE LEVEL : il s’agit du réglage du niveau d’amplitude affiché au sommet du réticule en dBm, dBµV, dBmV, V ou W. Cette amplitude représente donc une puissance ou une tension.
• AMPLITUDE LOG dB/DIV : il s’agit d’une graduation logarithmique de l’échelle verticale du réticule pour exprimer l’amplitude en dB par division : 10 ; 5 ; 2 ; 1 dB/Div par exemple. Ce rapport en dB par division indique celui entre le niveau d’amplitude du signal mesuré et le niveau absolu d’amplitude au sommet de l’écran (Reference Level).
• AMPLITUDE LINEAR : détermine une graduation linéaire d’amplitude.

Fig. 20 : Analyseur de spectre HP 8563E : fonctions principales Frequency, Span et Amplitude.

Quelles sont les indications affichées sur l’écran de l’analyseur de spectre ?

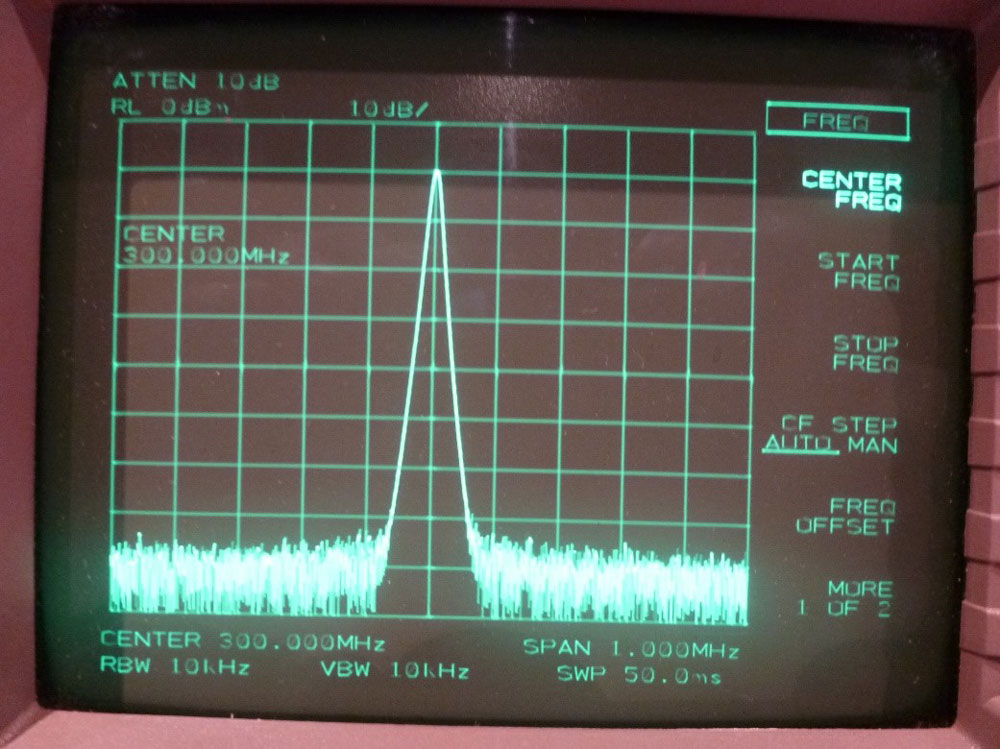
Fig. 21 : Écran afficheur du tube cathodique de l’analyseur de spectre HP 8563E.  Sur la droite de l’écran apparaissent les fonctions secondaires liées aux fonctions principales Frequency, Span, Amplitude.  Les fonctions secondaires sont sélectionnées par des touches de fonction qui sont alignées en regard des fonctions secondaires (principe des menus).

Afin de relever les clichés d’écran, un ordinateur portable est raccordé à l’analyseur de spectre par l’intermédiaire d’une interface GPIB-USB.

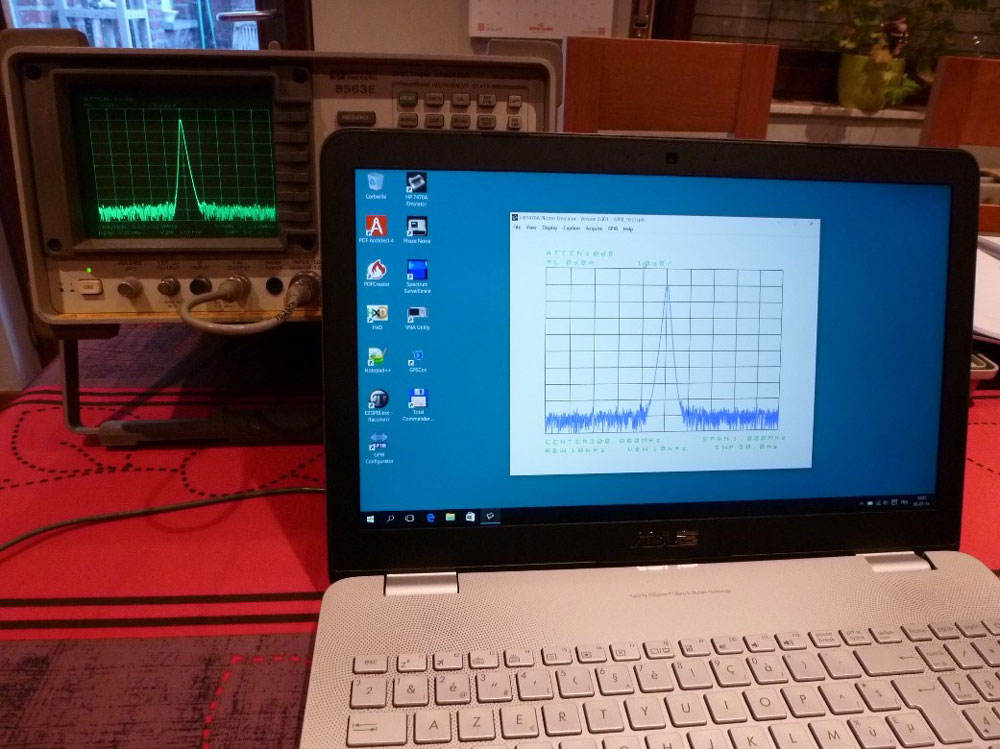
Fig. 22 : Liaison GPIB de l’analyseur de spectre HP8563E avec une entrée USB d’un ordinateur portable afin d’effectuer des relevés d’écran.  Le logiciel d’acquisition est l’émulateur de table traçante HP7470 qui a été réalisé par John Miles KE5FX.  L’interface GPIB-USB utilisée ici est un produit du constructeur Prologix.

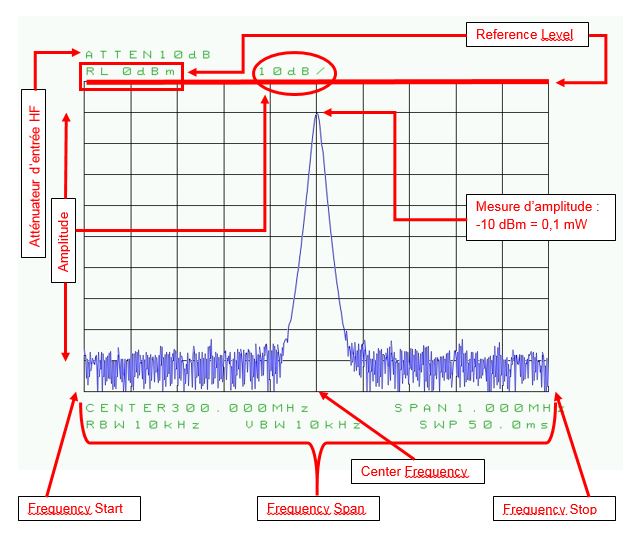
Fig. 23 : Relevé de l’affichage des données de mesure sur l’écran de l’analyseur de spectre : atténuateur d’entrée haute fréquence (ici de 10 dB), Center Frequency, Frequency Start Stop, Span, Reference Level, Log 10 dB par division, etc.

Le Frequency Span sur la figure ci-dessus étant de 1 MHz, on a 100 kHz par division horizontale.  Le Reference Level étant à 0 dBm et la graduation d’amplitude étant de 10 dB par division, la puissance du signal mesuré ici à 300 MHz est de -10 dBm, soit 0,1 mW.  La fréquence centrale étant de 300 MHz et le Span étant de 1MHz, on a un balayage en fréquence de l’analyseur de spectre entre 299,5 MHz et 300,5 MHz.

Nous avons d’autres indications importantes au bas de l’écran : RBW, VBW et SWP :

• RBW  (Resolution BandWidth) : sélectivité réglée à l’analyseur de spectre ;
• VBW (Video BandWidth) : filtrage du signal vidéo de la trace sur l’écran ;
• SWP (Sweep) : vitesse du balayage en fréquence de l’analyseur de spectre.

Ces paramètres RBW, VBW et SWP sont intimement liés et doivent faire l’objet d’un compromis entre eux.  Ils sont automatiquement mis en relation par les algorithmes programmés dans l’unité centrale de calcul de l’analyseur de spectre.  Toutefois, il est possible de débrayer cet automatisme et de sélectionner ces paramètres manuellement.
Le réglage manuel de la sélectivité de l’analyseur de spectre (RWB) ne peut être réduit impunément sans tenir compte du temps de montée et de descente d’un signal lors de son passage à travers les filtres passe-bande de la moyenne fréquence.  Ainsi le signal doit être appliqué pendant un certain temps dans la bande passante du filtre passe-bande afin d’obtenir un signal correctement traité sans distorsion de celui-ci ni dégradation de son amplitude.  L’analyseur de spectre balaye en permanence une plage de fréquence, dès lors le signal « passe » fugitivement au travers du filtre passe-bande, et en particulier dans sa bande passante.  Cette « vitesse » de passage du signal est fonction du paramètre SPAN (étalement en fréquence) et de la vitesse de balayage SWEEP de l’analyseur de spectre entre la fréquence Start et Stop.  Selon le réglage de la résolution de bande passante (RBW) de l’analyseur, le temps de montée du signal est différent : ce temps est allongé pour une résolution plus fine, c’est-à-dire pour un filtre passe-bande à bande plus étroite que celle qui avait été choisie au départ.  En outre, plus le filtre est à bande étroite, moins de temps met le signal pour passer d’une extrémité à l’autre de la bande passante du filtre selon le balayage de l’analyseur.

On peut exprimer le temps que le signal doit rester dans la bande passante du filtre comme suit :

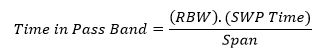
D’autre part, le temps de montée du signal dans un filtre est inversement proportionnel à sa bande passante.

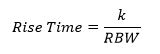
Si on établit une équivalence entre ces deux équations, on obtient :

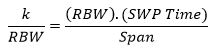
C’est-à-dire :

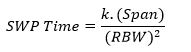
Les filtres passe-bande peuvent avoir différentes formes de courbes de réponse selon le type de filtre.  Dans les analyseurs de spectre, on utilise généralement des filtres passe-bande du type Quasi-Gaussien pour lesquels la valeur k est de l’ordre de 2 à 3.
L’information qu’il y a lieu de retenir ici est que tout changement dans la résolution de bande passante de l’analyseur de spectre a un effet drastique sur la vitesse de balayage (Sweep Time).  Dans les analyseurs classiques, les calibres de résolution évoluent selon une séquence 1, 3, 10, soit une séquence dont l’évolution équivaut grossièrement à la racine carrée de 10.  Ainsi, le temps de balayage (Sweep Time) est affecté d’un facteur 10 à chaque saut de calibre de résolution de bande passante de l’analyseur (voir le dénominateur de l’équation ci-dessus qui est le carré de RBW).

Si le temps de balayage est trop court, l’analyseur indique un message d’erreur : « Meas Uncal », c’est-à-dire que la mesure n’est pas valide ou non calibrée.
Les calibres RBW (résolution) et VBW (filtre vidéo) sont en général automatiquement liés entre eux par un facteur 1, mais il est possible d’effectuer un réglage manuel de la bande passante vidéo (VBW) qui sera le plus souvent d’une bande plus étroite que celle de la résolution (RBW).

Pourquoi la théorie nous apprend qu’une porteuse doit être visible sous la forme d’une raie et qu’en pratique un analyseur de spectre montre une courbe en forme de cloche ?

Il faut se rappeler que notre analyseur de spectre est avant tout un récepteur superhétérodyne à changement de fréquence et ceci explique la raison pour laquelle la réponse en fréquence du signal est d’une largeur de bande définie (voir schéma bloc de la figure 4).  En effet, le résultat du changement de fréquence à la sortie du mélangeur inclut la somme et la différence entre le signal HF d’entrée et de celui de l’oscillateur local (hétérodyne), mais on y retrouve aussi les deux signaux eux-mêmes, c’est-à-dire le signal HF et celui de l’oscillateur local.  Un filtre passe-bande détermine la fréquence du signal désiré et rejette ainsi les autres signaux, en particulier celui qui est issu de la fréquence image du changement de fréquence.  Comme la fréquence du signal HF est fixe et que c’est l’oscillateur local qui effectue le balayage en fréquence, le produit du changement de fréquence subit lui aussi un balayage en fréquence.  Si un signal qui est produit par le changement de fréquence passe par le filtre passe-bande de l’étage de la moyenne fréquence, c’est la forme de la courbe de réponse du filtre passe-bande moyenne fréquence qui sera tracée sur l’écran de l’analyseur de spectre.  Le filtre de bande passante la plus étroite détermine celle qui est tracée sur l’écran.  Cette bande passante la plus étroite définit la résolution de bande passante de l’analyseur de spectre (RBW).

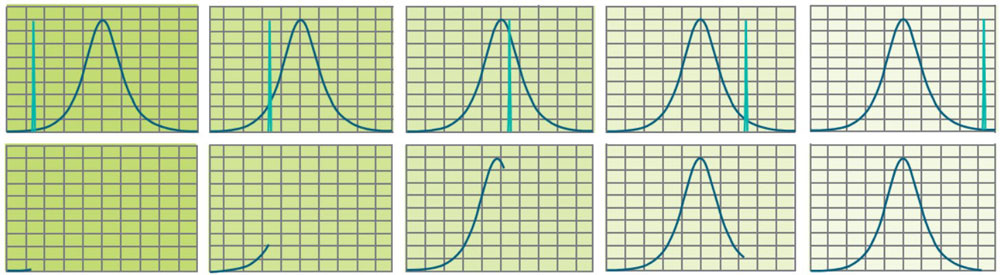
Fig. 24 : Lorsqu’un signal qui est le produit du changement de fréquence sous forme de raie balaye la bande passante du filtre passe-bande du filtre moyenne fréquence, c’est la courbe de réponse du filtre passe-bande qui est tracée sur l’écran de l’analyseur de spectre.  Source Agilent AN-150.

Si on injecte deux signaux à haute fréquence d’égale amplitude à l’entrée de l’analyseur de spectre et que ces signaux sont séparés entre eux d’une certaine différence de fréquence, alors il y a lieu de régler la résolution de bande passante de l’analyseur de façon à bien distinguer les deux signaux.  Autrement dit, la RBW doit être réglée à une bande passante (définie à -3 dB) égale ou inférieure à la valeur de l’écart en fréquence entre les deux signaux à haute fréquence.  Voyons cela.

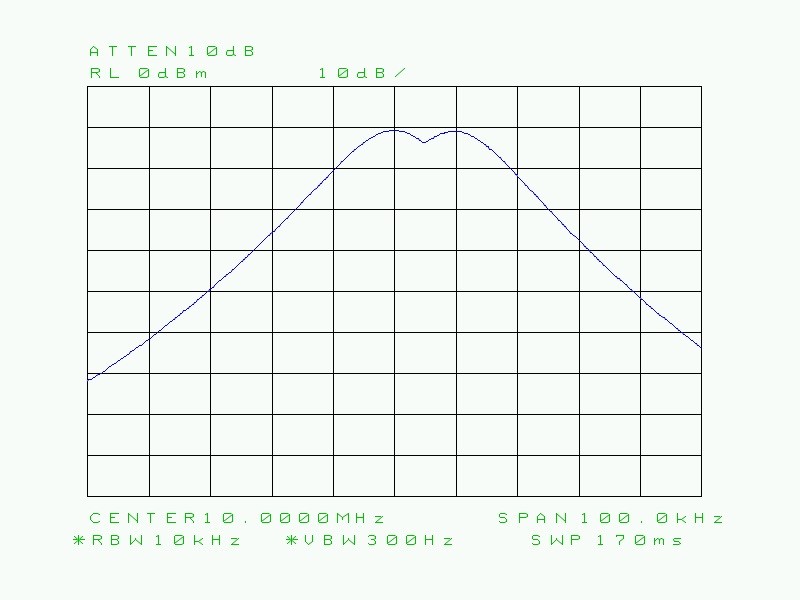
Fig. 25 : Deux porteuses HF (10,000 MHz et 10,010 MHz) RBW de 10 kHz.  La résolution est juste suffisante pour distinguer les deux signaux (le croisement des courbes se situe à -3 dB).

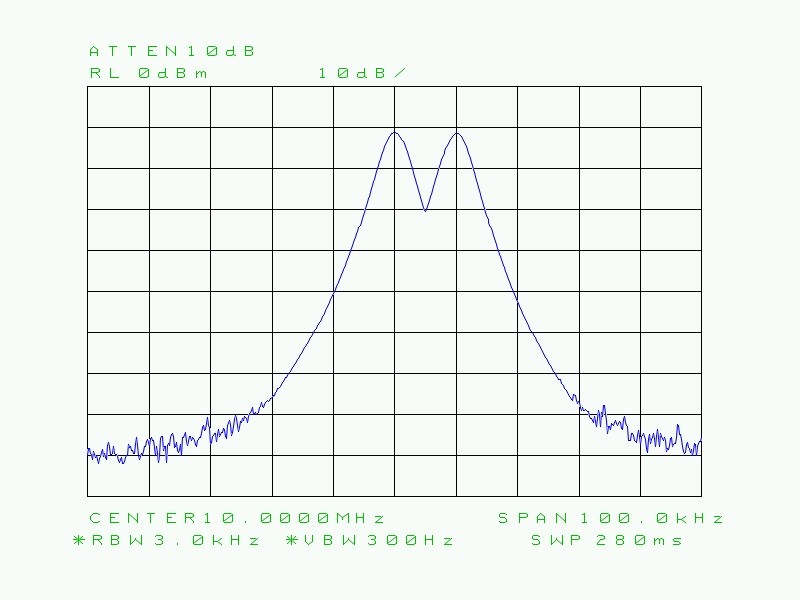
Fig. 26 : Idem ci-dessus mais avec une RBW de 3 kHz.  On commence à mieux distinguer les deux porteuses.

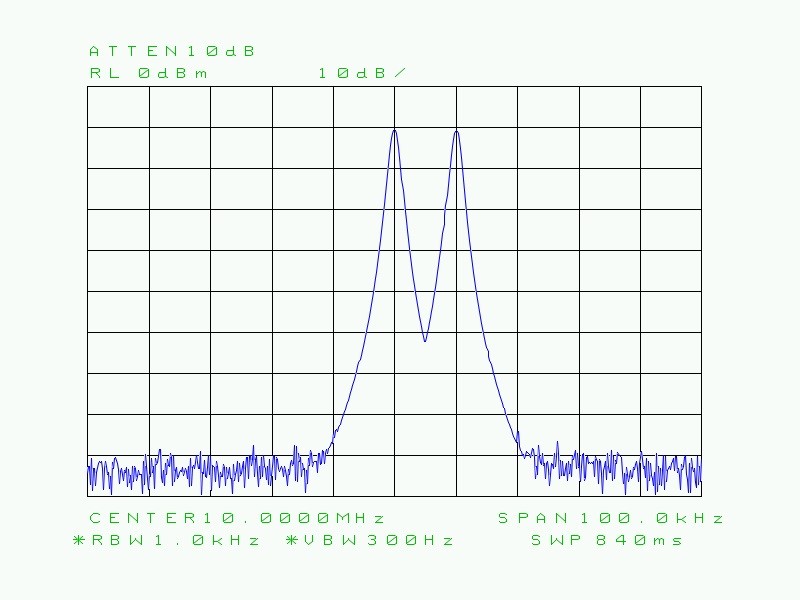
Fig. 27 : Idem ci-dessus mais avec une RBW de 1 kHz.  On distingue encore mieux les deux porteuses.

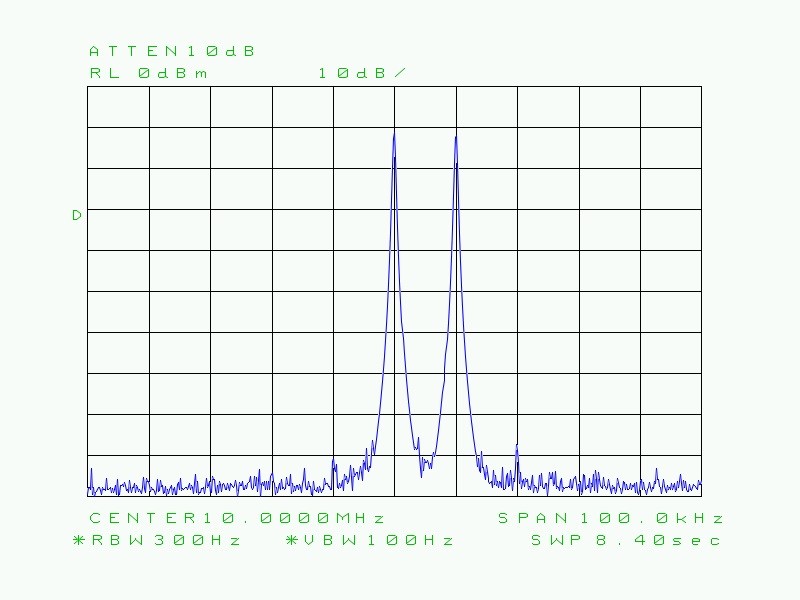
Fig. 28 : Idem ci-dessus mais avec une RBW de 300 Hz.  On distingue parfaitement les deux porteuses.

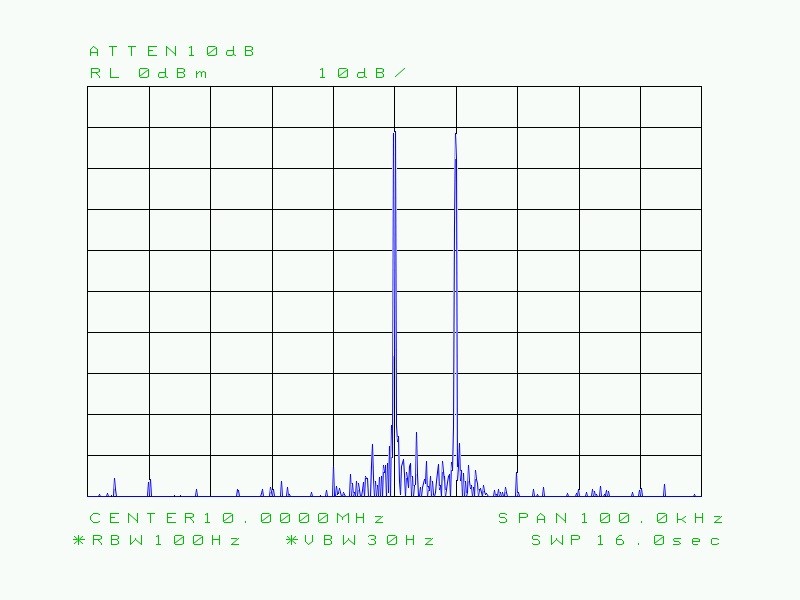
Fig. 29 : Idem ci-dessus mais avec une RBW de 100 Hz.  On distingue les deux porteuses et on commence à apercevoir un léger bruit de phase et une intermodulation du troisième ordre mais d’un niveau négligeable.  L’intermodulation provient d’une interaction entre les deux générateurs des porteuses : le combinateur des deux signaux n’offre pas une isolation HF suffisante entre les générateurs.

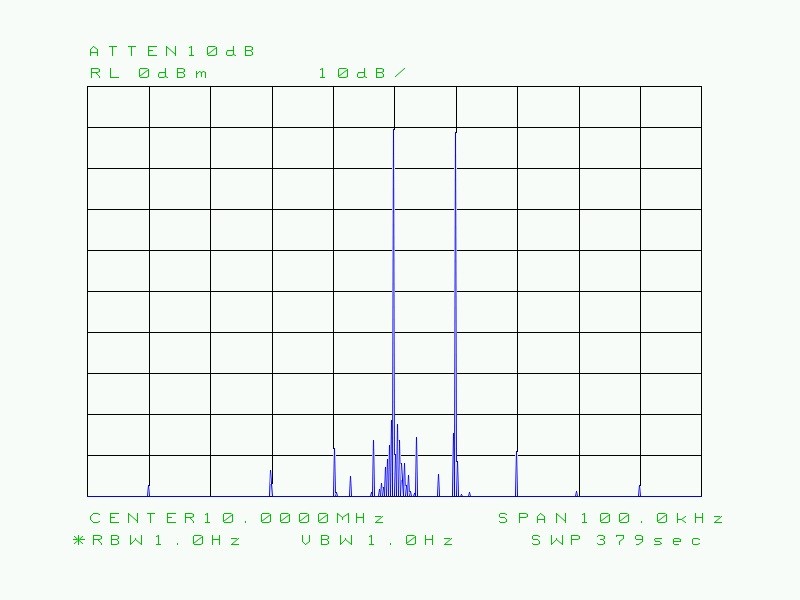
Fig. 30 : Idem ci-dessus mais avec une RBW de 1 Hz, c’est-à-dire la résolution la plus fine dans les capacités de l’analyseur de spectre.  On distingue mieux les produits d’intermodulation mais ceux-ci sont à un niveau d’amplitude d’environ -70 dBc (par rapport aux porteuses).

On comprend mieux à présent que la courbe tracée en forme de cloche (courbe gaussienne) est fonction de la RBW (bande passante du filtre moyenne fréquence).  On constate que le temps de balayage est passé au fur et à mesure de 170 ms à 280 ms, ensuite à 840 ms, puis à 8,4 s, à 16 s et enfin à 379 s pour une RBW extrême de 1 Hz.
La plupart du temps, nous observons des signaux proches l’un de l’autre en fréquence mais d’amplitudes différentes avec un rapport de plusieurs dizaines de décibel d’écart en amplitude.  C’est dans ce cas de figure que se révèle toute l’utilité du réglage de la résolution de l’analyseur de spectre (RBW).  En effet, si la RBW n’est pas suffisante, le signal le plus faible risque d’être masqué à l’écran de l’analyseur par le signal le plus fort.  La raison de ce phénomène de masquage est due à la forme de la courbe de réponse des filtres passe-bande de la chaîne moyenne fréquence, et en particulier de leur « raideur » de sélectivité (skirt, selectivity, shape factor).  Celle-ci s’exprime sous la forme d’un rapport entre la bande passante du filtre à -60 dB et celle à -3 dB comme illustré ci-dessous.

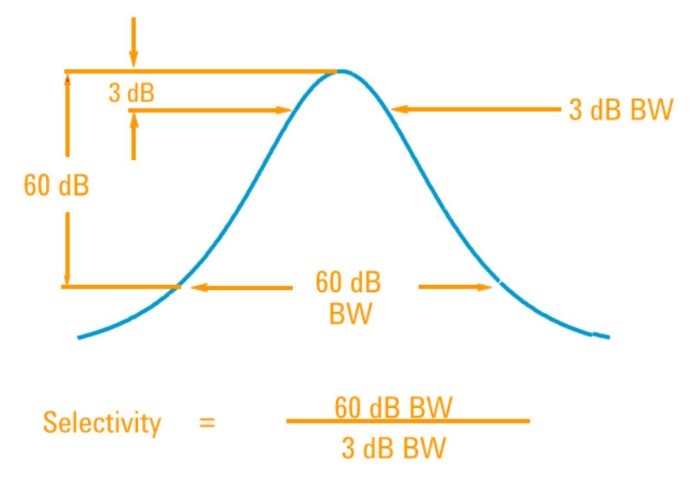
Fig. 31 : Expression de la sélectivité d’un filtre passe-bande.  Source Agilent.

Les filtres gaussiens analogiques classiques ont une sélectivité de l’ordre de 15:1 en revanche les analyseurs haut de gamme disposent de filtres numériques dans la chaîne moyenne fréquence qui porte ainsi la sélectivité à un rapport inférieur à 5:1.  Ces filtres numériques sont en général activés pour les résolutions de 100 Hz, 30Hz, 10 Hz, 3 Hz et 1 Hz.

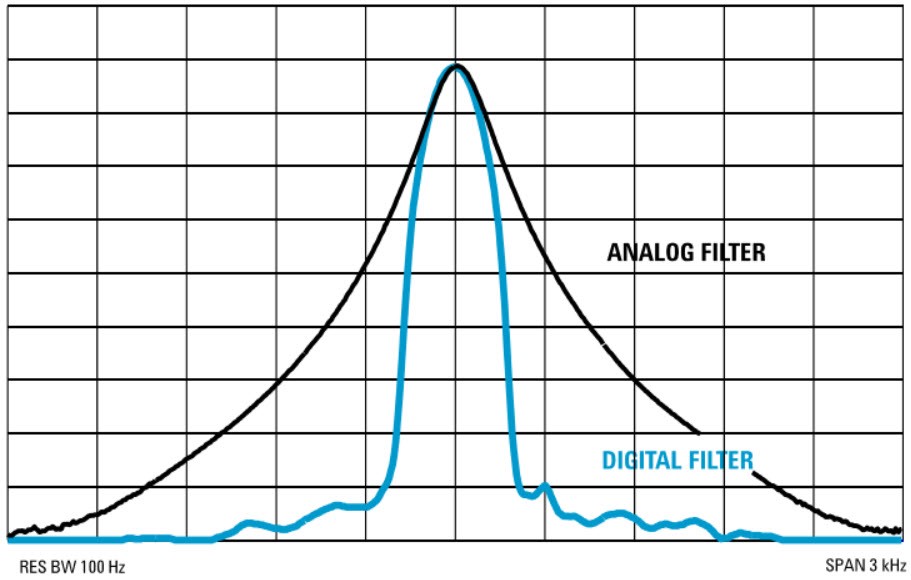
Fig. 32 : Différence de rapport de sélectivité des filtres passe-bande analogiques et numériques.  Source Agilent.

Voici ci-dessous un exemple de signaux proches en fréquence (écart de 10 kHz) et d’amplitudes différentes (50 dB de différence d’amplitude).

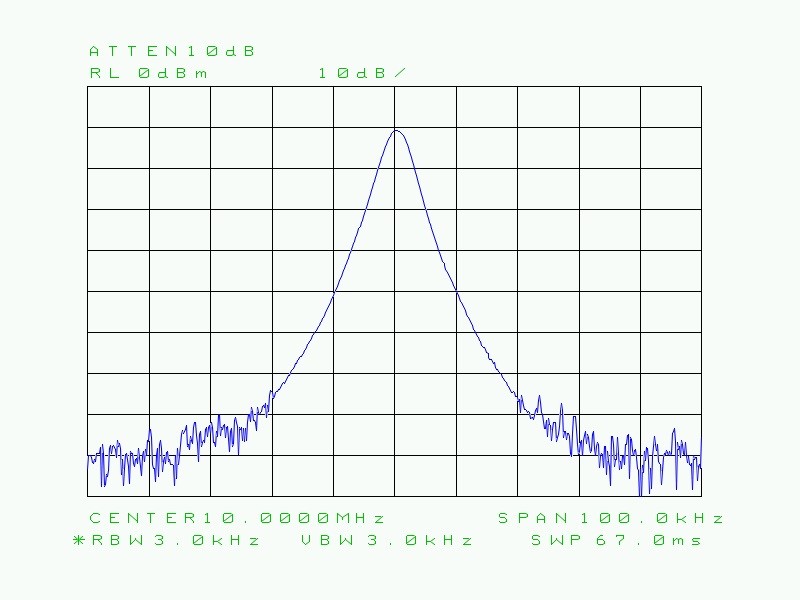
Fig. 33 : Deux porteuses HF (10,000 MHz et 10,010 MHz), Span 100 kHz, RBW de 3 kHz.  La résolution n’est pas suffisante pour détecter la présence d’une deuxième porteuse à environ -50 dB de la première.  La présence de la deuxième porteuse est représentée artificiellement en trait discontinu.

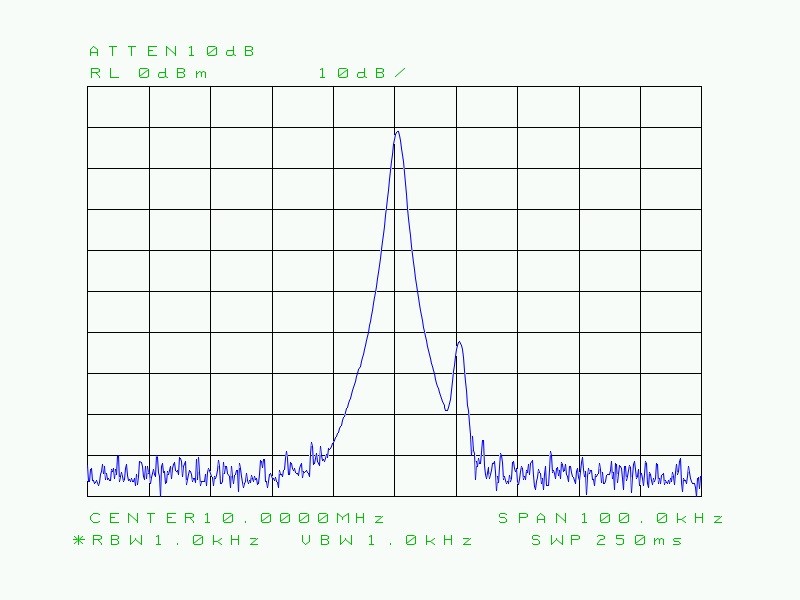
Fig. 34 : Même situation que ci-dessus, mais la résolution plus fine, RBW de 1 kHz fait apparaître les deux signaux.  Le trait discontinu représente artificiellement la première porteuse comme si elle avait été relevée avec une RBW de 3 kHz : le pic de la deuxième porteuse se situe en dessous de la courbe en trait discontinu.

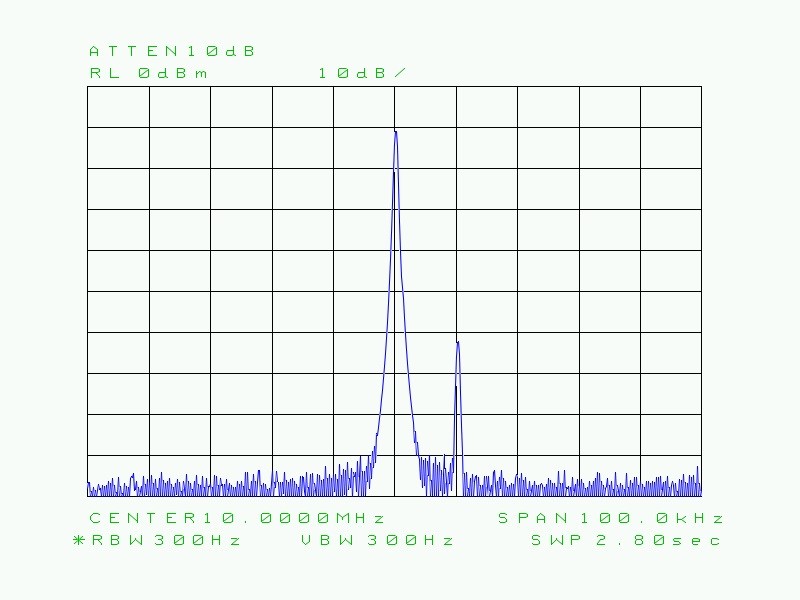
Fig. 35 : Même situation que ci-dessus, mais avec une RBW de 300 Hz.  Les deux signaux sont parfaitement distincts et identifiables.

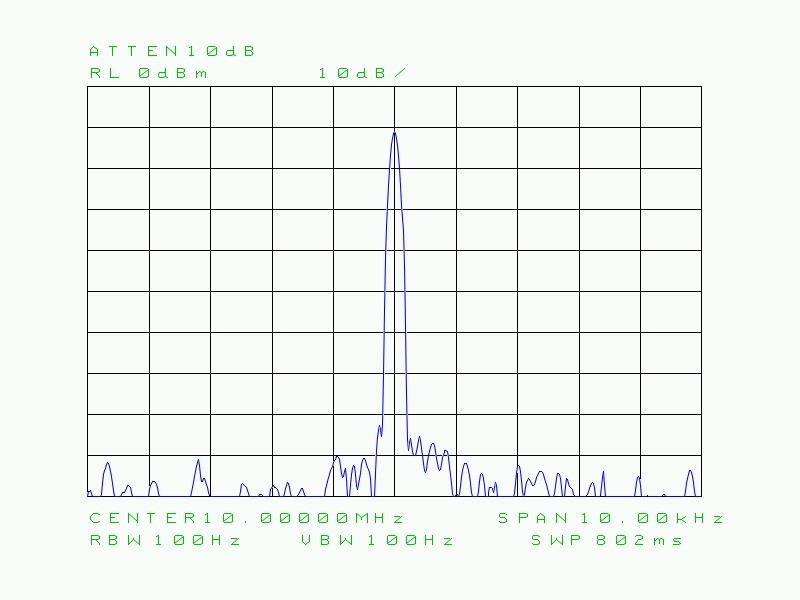
Fig. 36 : Porteuse seule de 10 MHz, Span 10 kHz (1 kHz par division).  Le réglage RBW de 100 Hz donne une trace selon la courbe de réponse d’un filtre très sélectif.  Il s’agit ici d’un filtre numérique de rapport de sélectivité de 5:1.  Les filtres numériques sont activés pour les réglages de RBW de 1 Hz, 3 Hz, 10 Hz, 30 Hz et 100 Hz.  À partir d’une résolution (RBW) de 300 Hz jusqu’à 2 MHz, les filtres sont analogiques et ont un rapport de sélectivité de 15:1.  (Voir figure 32).  L’avantage des filtres numériques est de permettre d’observer des petits signaux directement aux abords d’une fréquence porteuse (rayonnements non essentiels ou non désirés par exemple).

À quoi sert le filtre vidéo (VBW)

Le filtre vidéo est un filtre passe-bas qui est placé après le détecteur d’enveloppe de l’analyseur de spectre (voir figure 4).  Il sert essentiellement à lisser la courbe tracée sur l’écran.  Cela se révèle particulièrement utile pour mettre en évidence des signaux de très faibles amplitudes et relativement proches du niveau de bruit relatif aux conditions et paramètres de mesure.  Les caractéristiques de temps de montée du signal à travers le filtre vidéo a pour conséquence de devoir augmenter le temps de balayage de l’analyseur de spectre, en particulier si le calibre de la VBW est réglé manuellement à une valeur inférieure à celle du calibre de la RBW.

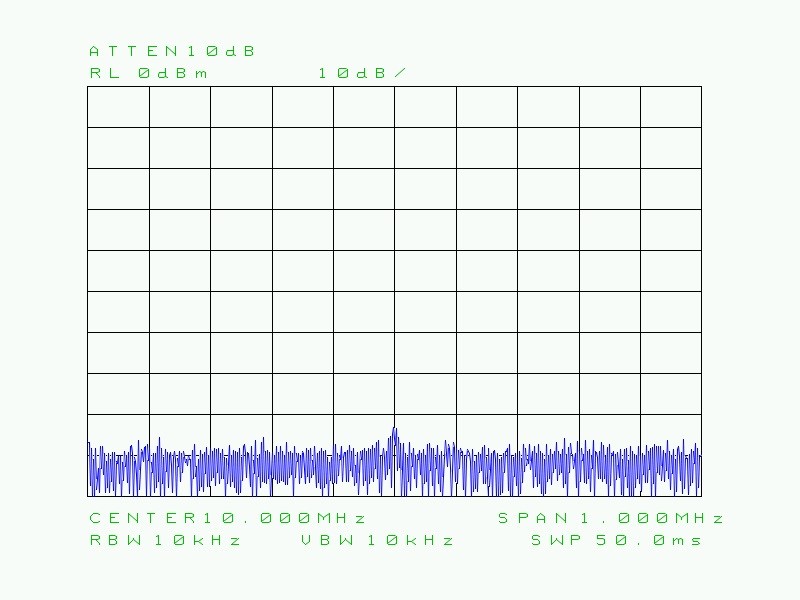
Fig. 37 : Porteuse 10 MHz d’amplitude de -87 dBm très peu discernable sans filtrage vidéo énergique.  Ici le filtre vidéo est réglé en automatique sur le calibre de 10 kHz.  Sweep Time : 50 ms.

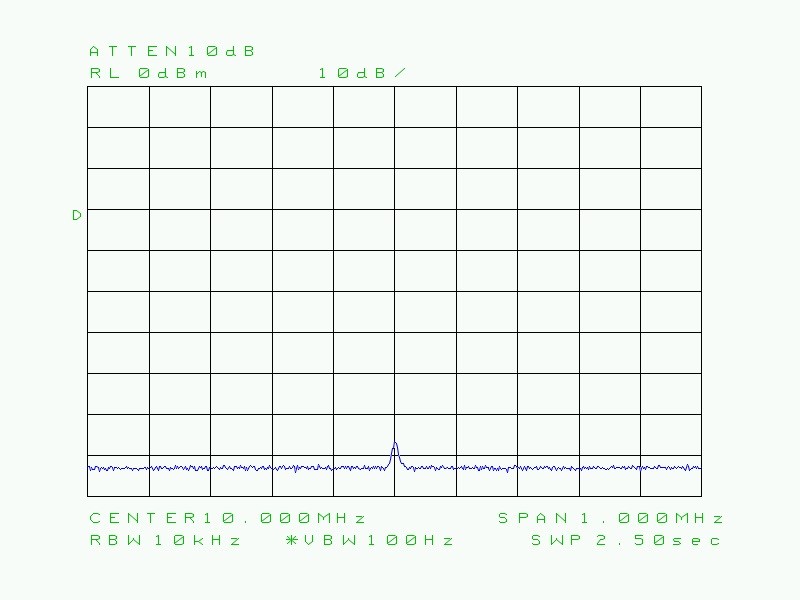
Temps de balayage pour VBW < RBW :

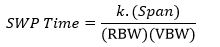
Fig. 38 : Idem ci-dessus, porteuse à -87 dBm, mais parfaitement discernable avec une VBW réduite manuellement sur le calibre de 100 Hz.  Sweep Time : 2,5 s.

Une alternative à l’utilisation du filtre vidéo analogique existe-t-elle ?

Oui : il s’agit de la technique du calcul de la moyenne des valeurs du signal vidéo numérisé (Video Averaging ou Trace Averaging).  L’analyseur de spectre calcule en permanence la moyenne du signal mesuré sur un nombre paramétrable de plusieurs balayages successifs.  Ceci a l’avantage de ne pas devoir allonger d’une manière excessive le temps du balayage en fréquence de l’analyseur.

La moyenne du signal vidéo est calculée point par point sur les valeurs d’amplitude du signal lors des balayages successifs en fréquence.  Ceci suppose que le dispositif afficheur à l’écran de l’appareil de mesure soit basé sur une technologie numérique : le signal analogique à la sortie du détecteur d’enveloppe est converti en signal numérique par l’intermédiaire d’un convertisseur analogique–numérique (ADC : Analog to Digital Converter). Ainsi, à chaque point affiché à l’écran, la nouvelle valeur d’amplitude moyennée est calculée en fonction de la valeur d’amplitude de ce point lors du balayage précédent.  L’algorithme de calcul est classique pour établir une moyenne glissante sur un nombre défini de différentes valeurs successives :

Pour la plupart des signaux à analyser, l’utilisation du filtre vidéo ou l’activation du calcul de la moyenne du signal vidéo numérisé donne des résultats pratiquement identiques.  C’est le cas pour des mesures de signaux de faibles amplitudes et qui sont proches du niveau du bruit.  Toutefois, il existe une différence fondamentale entre les deux principes de lissage de la courbe du signal mesuré.  Le filtre vidéo a pour effet d’effectuer un lissage en temps réel : on constate son effet immédiat sur chaque point de la courbe au cours du balayage ; les valeurs à chaque point sont « moyennées » une seule fois à chaque balayage.  En revanche, le calcul de la moyenne des valeurs du signal vidéo numérisé requiert plusieurs balayages afin d’obtenir la valeur qui converge vers le résultat de ce calcul.

Lorsqu’on observe un signal qui fluctue au cours du temps (signal modulé en fréquence d’une station radio, par exemple), les deux techniques (VBW et Averaging) présenteront des résultats différents : le filtrage vidéo analogique (VBW) donnera une moyenne différente à chaque balayage ; le calcul numérique de la moyenne (Averaging) donnera après n balayages un résultat bien plus proche de la vraie moyenne, comme illustré ci-dessous.

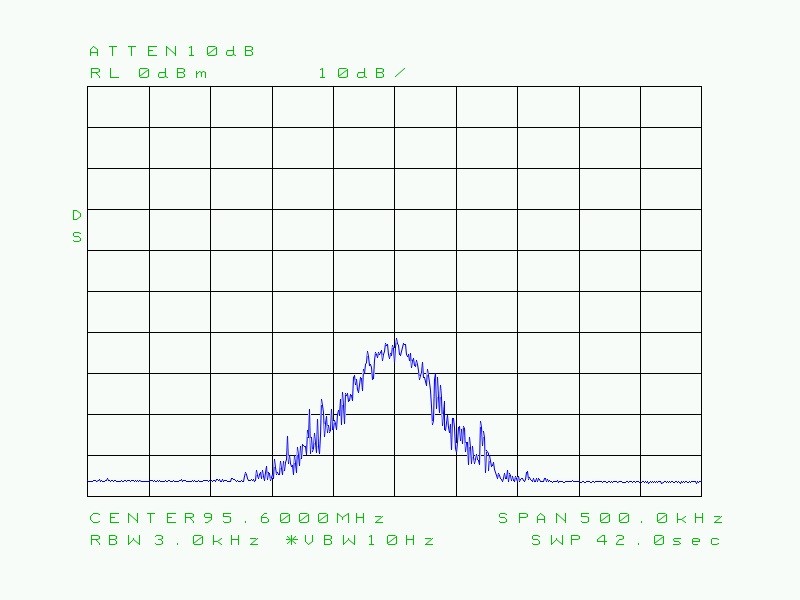
Fig. 39 : Illustration de l’effet du filtrage vidéo analogique énergique sur un signal modulé en fréquence d’une station de radiodiffusion de la bande FM 95,6 MHz.  RBW = 3 kHz ; VBW = 10 Hz ; SWP = 42 s.

Fig. 40 : Illustration de l’effet du calcul numérique de la moyenne du signal vidéo sur le même signal FM 95,6 MHz.  RBW = 3 kHz ; VBW = 3 kHz ; Averaging : n = 100 ; SWP = 140 ms ; 100 x 0,14s = 14 s.

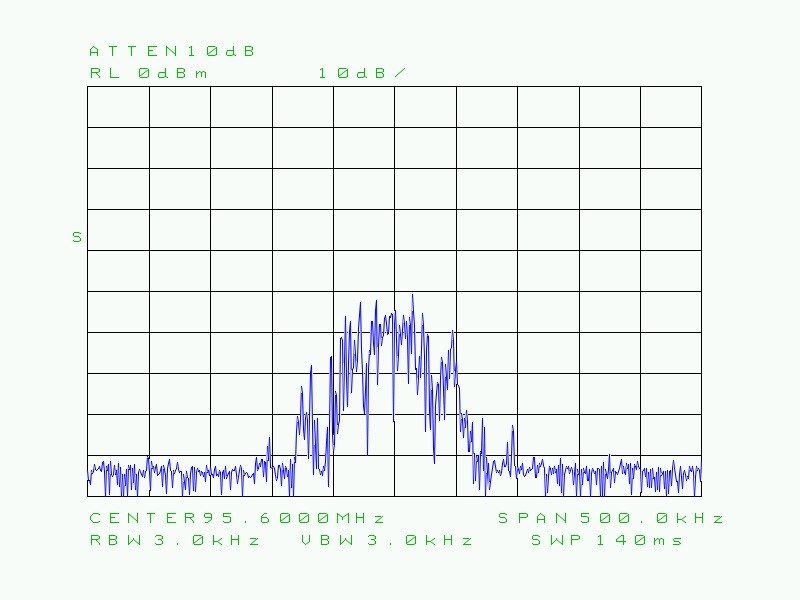
Fig. 41 : Même signal que celui des deux clichés précédents ci-dessus (FM 95,6 MHz) mais sans filtrage vidéo analogique énergique ni calcul numérique de la moyenne du signal vidéo.

Il existe une autre fonction utile pour traiter le signal vidéo lorsque l’on est en présence d’un signal modulé et dont la modulation fluctue au cours du temps : il s’agit de la fonction TRACE MAX HOLD.  Cette fonction se révèle utile pour observer les pointes de modulation en mémorisant leurs maximums (maxima).  On peut ainsi relever l’enveloppe qu’occupe un signal modulé et vérifier si le signal dans la bande nécessaire ne déborde pas sur un canal adjacent.

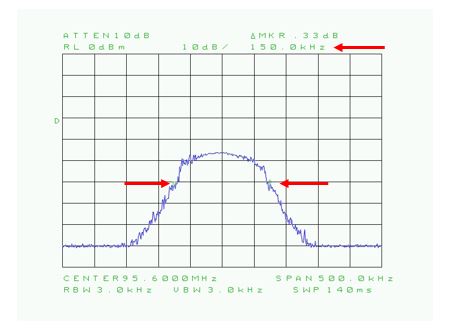
Fig. 42 : Même signal que celui des trois clichés précédents ci-dessus (FM 95,6 MHz) mais avec activation de la fonction TRACE MAX HOLD.  Pour cet émetteur, la modulation est optimale et la déviation maximale de fréquence se situe bien dans la norme ±75 kHz (largeur de 150 kHz) des stations de radiodiffusion de la bande FM (voir l’indication des deux marqueurs de fréquence).

Résumons par quelques mots clefs ce que nous avons appris jusqu’à présent sur l’analyseur de spectre

L’analyse spectrale est l’étude d’un signal dans le domaine de la fréquence.  Elle est utile pour analyser une émission d’une station radioamateur quant à sa pureté spectrale au point de vue de la fréquence porteuse, de sa modulation dans la largeur de bande nécessaire, des harmoniques de la porteuse, des rayonnements parasites non essentiels et non désirés.  Nous nous sommes familiarisés avec les notions de balayage en fréquence, Center Frequency, Frequency Start et Stop, Amplitude, Reference Level, Log dB/Div, Linear, Span, RBW (Resolution BandWidth), VBW (Video BandWidth), Averaging, Sweep Time, changement de fréquence, moyenne fréquence, fréquence image, filtre passe-bande analogique et numérique, rapport de sélectivité, VCO, PLL, OCXO, YTO, etc.  C’est déjà un bon début.

Nous avons toutefois passé sous silence quelques cases du schéma bloc d’un analyseur de spectre...

Cet article peut être téléchargé au format PDF. Il suffit de cliquer sur ce lien :

A propos de l'auteur