L’abaque de Smith : un outil mystérieux ? Un outil démystifié !

Dans le domaine de la radiofréquence, l’adaptation d’impédance, le rapport d’ondes stationnaires et le coefficient de réflexion sont des notions primordiales pour assurer le maximum de transfert de puissance entre une source et une charge. Les lignes de transmission sont indispensables pour canaliser l’énergie HF et la véhiculer sur une distance nécessaire par exemple pour le raccordement d’un émetteur à une antenne d’une station radioamateur. La distance, la fréquence et la vitesse de propagation des ondes sont étroitement liées par la notion de longueur d’onde. Les radioamateurs sont bien conscients de toutes ces notions relativement abstraites et en connaissent les applications pratiques pour assurer le fonctionnement optimum d’une station de radio-émission.
Un nouveau projet technique commence en général par un calcul d’ordre de grandeur pour établir des valeurs qui sont compatibles avec celles des composants électroniques à mettre en œuvre. Il est parfois nécessaire de procéder à plusieurs approximations successives pour pouvoir converger vers des résultats pratiques. Afin de garder une vue d’ensemble sur le projet, il est plus commode d’utiliser des abaques pour pouvoir cibler certains choix sans perdre le fil conducteur de ce à quoi nous voulons aboutir. Une fois que les premières valeurs repères sont acquises, il est toujours temps d’affiner certains résultats par un calcul analytique. Trouver un résultat du calcul analytique qui est cohérent avec le résultat qui est issus de l’utilisation d’un abaque contribue à augmenter notre coefficient de certitude sur la validité de ce résultat.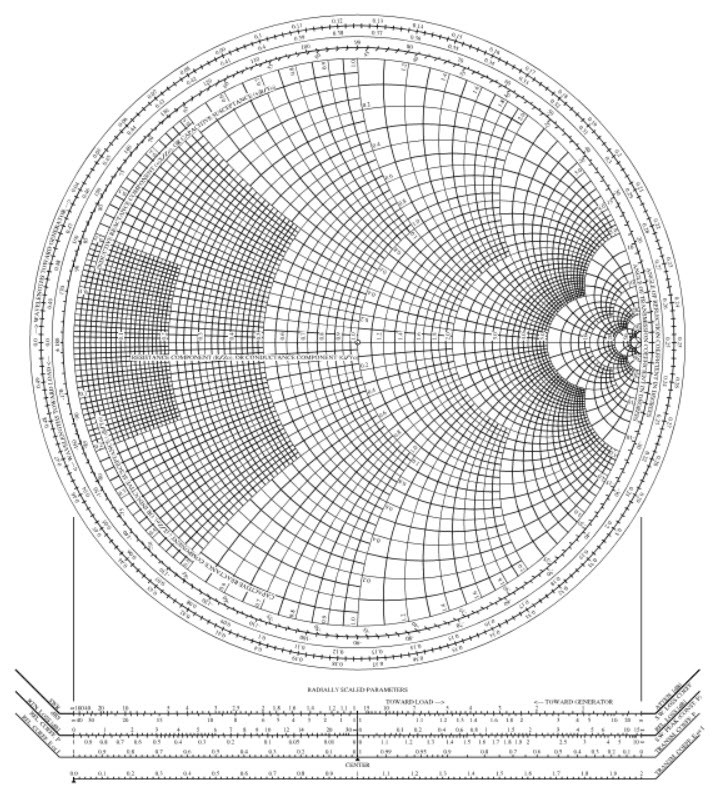

Fig. 1 : Abaque de Smith. Merci Mr. Phillip Hagar Smith : votre outil est très utile à de nombreuses générations d’électroniciens en télécommunication et à de nombreux radioamateurs depuis 1939.

Le but de cet article est d’avoir une prise de contact avec ce qu’est l’abaque de Smith et de montrer quelques facettes des possibilités pratiques que l’on peut en retirer. Nous ne prétendrons pas être exhaustifs sur ce sujet car les domaines d’applications sont vastes et s’étendent aux multiples expériences pratiques de chacun des radioamateurs. La compréhension de l’abaque de Smith nous sera utile pour aborder l’utilisation d’un analyseur de réseau vectoriel qui fera l’objet d’un futur article sur le site Internet ON5VL. Le contenu du début de cet article a été inspiré en partie par celui du chapitre 28 du livre ARRL Antenna Book 21th Edition sur le sujet de l’abaque de Smith. La suite de l’article a été inspirée par d’autres publications dont les sources seront mentionnées au fur et à mesure.

L’abaque de Smith a été établi par Phillip Hagar Smith en 1936 et publié en 1939 suite à ses travaux sur les lignes de transmission. P.H. Smith était un radioamateur très actif avec son indicatif 1ANB. À cette époque, les ingénieurs ne disposaient que de leur règle à calcul et des tables de logarithmes. Les calculs scientifiques étaient longs et fastidieux sans l’aide des outils modernes que nous connaissons aujourd’hui. C’est la raison pour laquelle P.H. Smith s’intéressait aux représentations graphiques des relations mathématiques. En 1969, il publia le livre Electronic Applications of the Smith Chart : In Waveguide, Circuit, and Component Analysis, un ouvrage complet sur le sujet de l’abaque qui porte son nom : c’est le livre de référence par excellence.

Bien que nous disposions aujourd’hui de calculatrices scientifiques et d’ordinateurs performants, l’abaque de Smith reste un outil actuel et largement utilisé à telle enseigne que les analyseurs de réseau vectoriels (y compris les plus modernes) disposent d’un affichage prévu avec abaque de Smith pour la mesure du coefficient de réflexion et celle des composantes de l’impédance complexe.

Fig. 2 : Analyseur de réseau vectoriel HP 8720A. Source : Wikipedia Smith Chart.

Nous supposons que le lecteur est déjà familiarisé avec les nombres complexes qui symbolisent en électrotechnique la partie résistive et la partie réactive d’une impédance. Lorsqu’on applique un signal alternatif aux bornes d’une réactance pure (un condensateur ou une bobine de self induction), on observe un déphasage de 90° entre la tension à ses bornes et le courant qui la traverse. Lorsqu’un signal est appliqué à une résistance pure, la tension et le courant sont en phase. Lorsqu’on a une combinaison d’une réactance avec une résistance, le déphasage peut être représenté graphiquement par les vecteurs de Fresnel et l’impédance complexe peut être représentée sur un plan appelé plan complexe comportant un axe X des nombres réels en abscisses (partie résistive) et un axe Y des nombres imaginaires en ordonnées (partie réactive).

Dans l’article « Analyseur de spectre et mesures scalaires » publié sur le site Internet ON5VL, nous nous sommes familiarisés avec la notion du coefficient de réflexion (Γ) et la relation qui le relie avec une impédance (Z_C) chargeant une ligne de transmission d’impédance caractéristique (Z₀). Le coefficient de réflexion et aussi relié au rapport d’ondes stationnaires, voir ci-dessous :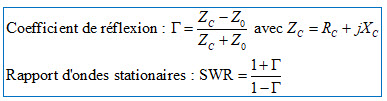

L’abaque de Smith est un outil graphique qui permet de résoudre des calculs de ligne de transmission, de circuits d’adaptation d’impédance etc., mais qui permet aussi d’afficher plusieurs paramètres comme l’impédance, l’admittance, le coefficient de réflexion, etc. Du point de vue mathématique, l’abaque de Smith représente toutes les impédances complexes en fonction des coordonnées polaires définies par le coefficient de réflexion dans un plan complexe (transformation bilinéaire de Moebius).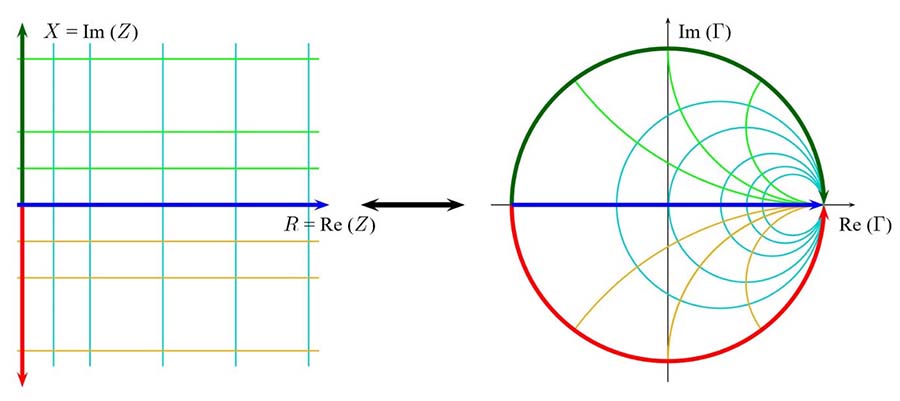

Fig. 3 : Transformation du plan complexe d’impédance Z en plan complexe du coefficient de réflexion Γ sur l’abaque de Smith (avec réseaux des cercles d’impédance). Source RF engineering basic concepts, Fritz Caspers, CERN, Geneva, Switzerland ; ARRL Pacific Division Convention 11-13 Oct. 2013, Santa Clara, California, USA.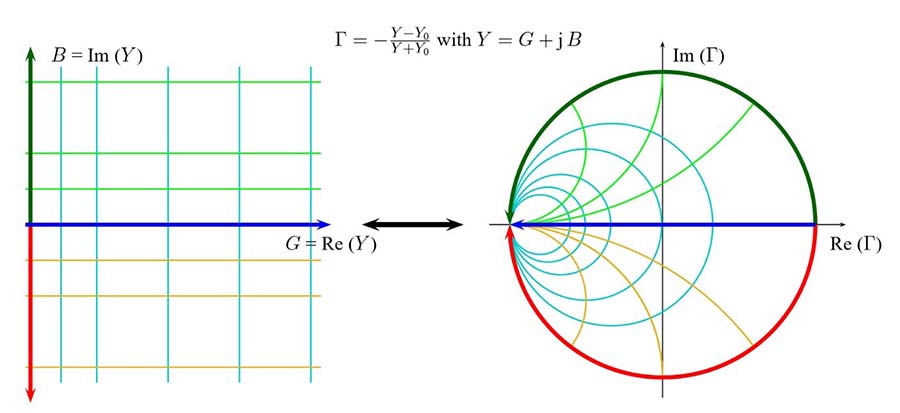

Fig. 4 : Transformation du plan complexe d’admittance Y en plan complexe du coefficient de réflexion Γ sur l’abaque de Smith (avec réseaux des cercles d’admittance). Source RF engineering basic concepts, Fritz Caspers, CERN, Geneva, Switzerland ; ARRL Pacific Division Convention 11-13 Oct. 2013, Santa Clara, California, USA.

L’abaque est utilisé en impédance normalisée de manière à pouvoir servir dans tous les cas de figure de système d’impédance, en général 50 Ω, mais aussi 75 Ω ou toute autre impédance qui est représentée au point central de l’abaque (Prime Center). Lorsqu’on a abouti à la solution du calcul, le résultat est « dé-normalisé » en le multipliant par l’impédance du système. Le coefficient de réflexion est lui directement lu sur l’abaque. Le pourtour de l’abaque est gradué en fraction de longueur d’onde ou en degré pour dimensionner la longueur d’onde électrique d’une ligne de transmission à partir de la charge en direction de la source (Toward Generator) ou à partir de la source en direction de la charge (Toward Load).

Comme l’impédance est fonction de la fréquence de travail, l’abaque est utilisé pour une seule fréquence à la fois. Toutefois, on peut tracer une courbe reliant plusieurs impédances à différentes fréquences constituant ainsi un lieu géométrique sur l’abaque. C’est en général le tracé de ce lieu qui est affiché sur l’écran d’un analyseur de réseau vectoriel.

L’abaque est constitué des réseaux de cercles pour les coordonnées d’impédance (Z) et des réseaux de cercles miroités pour les coordonnées d’admittance (Y). Ces réseaux peuvent aussi être tous les deux tracés en couleurs différentes sur le même abaque recevant ainsi l’appellation de « imittance » qui est le contracté des deux mots impédance et admittance (YZ).

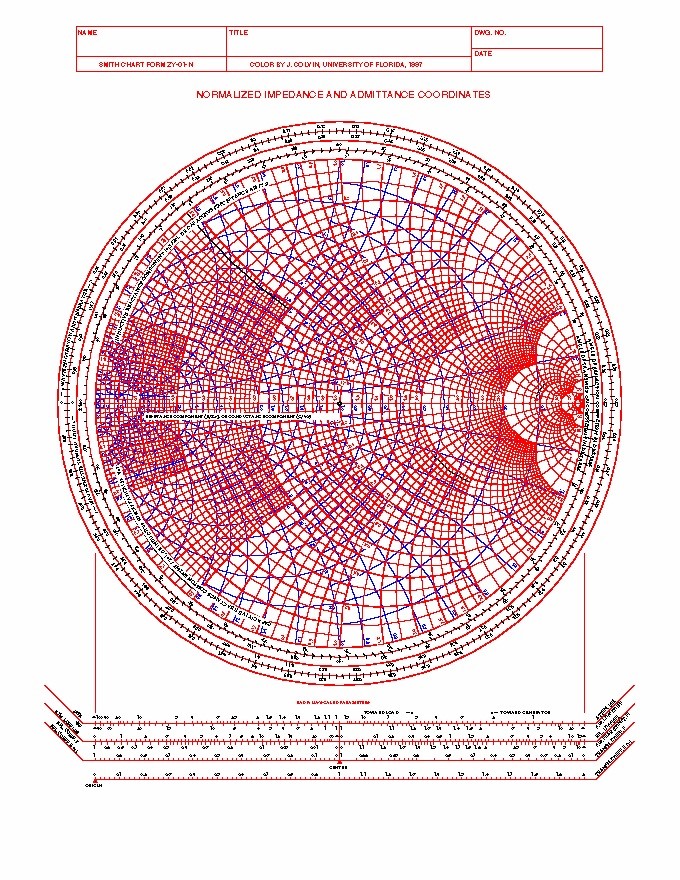
Fig. 5 : Abaque de Smith « imittance » : réseau de courbes d’impédance en rouge et réseau de courbes d’admittance en bleu.

Les relations mathématiques qui suivent vont nous être précieuses en pratique.

Impédance, admittance et normalisation :

L’admittance (Y) en [S] (Siemens) est tout simplement l’inverse de l’impédance (Z) en [Ω] (Ohm). Pour des raisons pratiques, lorsqu’on composera un réseau série, on travaillera en impédance car on effectue la somme des impédances. Lorsqu’on composera un réseau parallèle, on travaillera en admittance car on effectue la somme des admittances (l’inverse de l’impédance équivalente est la somme des inverses des impédances). L’inverse d’une résistance (R) est la conductance (G) ; l’inverse d’une réactance (X) est une susceptance (B). Une impédance (Z) devient normalisée (z) en la divisant par l’impédance du système (Z₀) ; une admittance (Y) devient normalisée (y) en la divisant par l’admittance du système (Y₀), ce qui revient à la multiplier par l’impédance du système. La notation des valeurs normalisées est par convention en lettres minuscules. Une impédance caractéristique de 50 Ω correspond à une admittance de 20 mS (20 milli-Siemens) et non pas 20 ms (20 milliseconde).

Inductance, capacitance, susceptance inductive, susceptance capacitive :

La réactance et la susceptance sont fonction de la fréquence (f) et donc de la pulsation (ω) avec ω = 2πf. En impédance complexe, une réactance ou une susceptance est un imaginaire pur ; c’est la raison pour laquelle elle est précédée de la notation « j ».

Valeurs des bobines d’induction et des condensateurs :

Points de repères sur l’abaque de Smith :

Le point central de l’abaque (Prime Center) représente le système d’impédance normalisée dans lequel on travaille. Celle-ci est en général l’impédance caractéristique de la ligne de transmission utilisée, par exemple Z₀ = 50 Ω qui une fois normalisée devient : 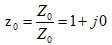c’est-à-dire une résistance pure normalisée de 1 Ω.

L’axe horizontal (X) de l’abaque représente des résistances pures : à l’extrémité gauche du cercle de contour l’impédance est z = 0 + j0 (impédance nulle = court-circuit) ; à l’extrémité droite, l’impédance est z = ∞ + j∞ (impédance infinie = circuit ouvert).

La région de l’abaque située au-dessus de l’axe X représente des impédances à réactance inductive (partie imaginaire positive de l’impédance complexe) ou des admittances à susceptance capacitive (partie imaginaire positive de l’admittance complexe); la région située en dessous de l’axe X représente des impédances à réactance capacitive (partie imaginaire négative de l’impédance complexe) ou des admittances à susceptance inductive (partie imaginaire négative de l’admittance complexe).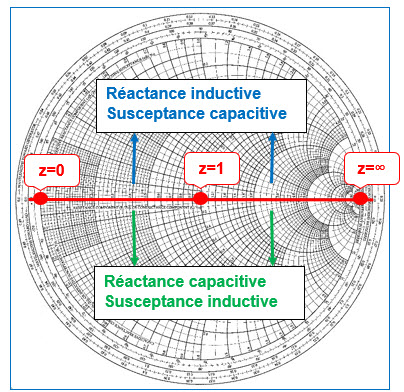

Fig. 6 : Axe X des résistances pures de zéro à l’infini et régions des réactances ou susceptances. Graphisme : ON4IJ.

Une impédance normalisée se situe sur l’abaque de Smith à l’intersection de deux arcs de cercle. Le premier arc fait partie d’un réseau de cercles à résistance normalisée constante ; le deuxième arc fait partie d’un réseau de cercles à réactance normalisée constante.

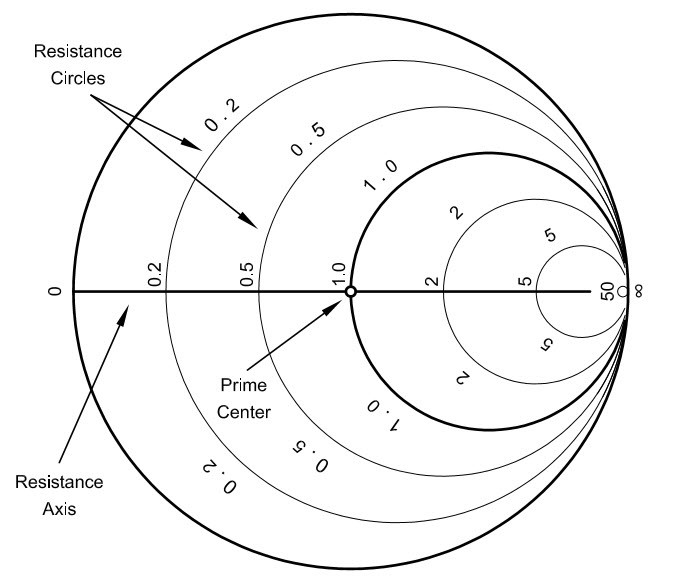
Fig. 7 : Réseau des cercles à résistance normalisée constante. Source ARRL Antenna Book 21^st Edition.

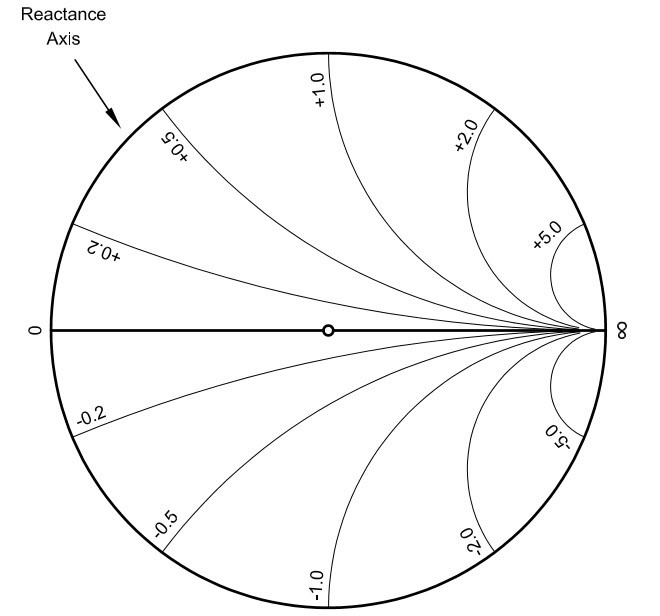
Fig. 8 : Réseau des cercles à réactance normalisée constante. Source ARRL Antenna Book 21^st Edition.

Il s’agit ici de segments d’arc de cercles : ceux-ci se prolongent en dehors de l’abaque.

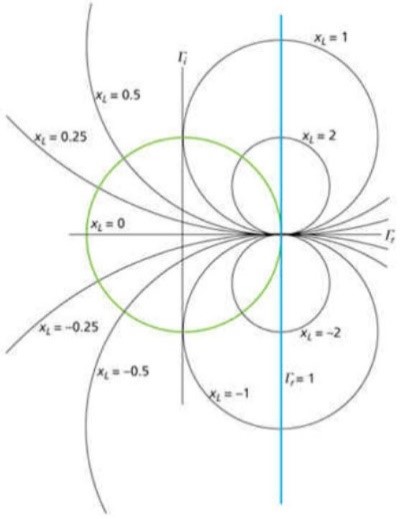
Fig. 9 : Prolongement des arcs de cercle à réactance normalisée constante. Source T&M World, July 2001 ; Rick Nelson.

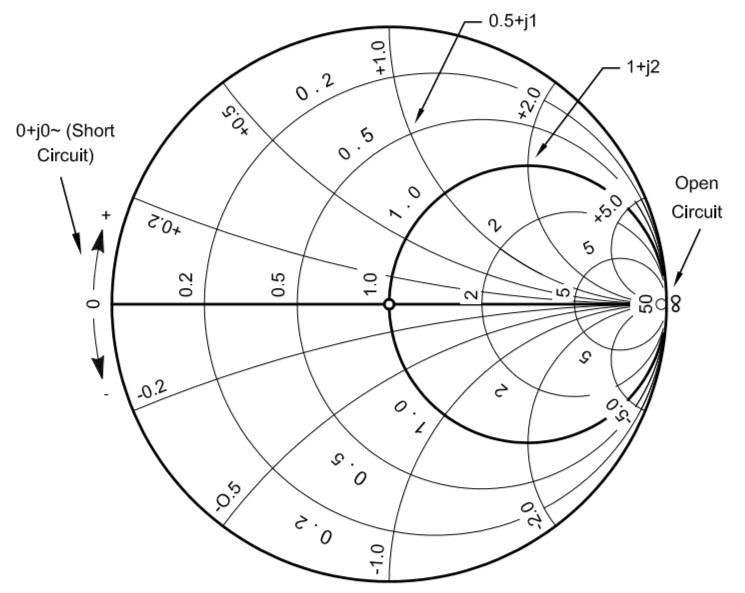
Fig. 10 : Système complet de coordonnées d’impédances normalisées sur l’abaque de Smith avec deux exemples d’impédances inductives. Source ARRL Antenna Book 21^st Edition.

1^er exemple : z = 0,5 + j1 en valeur normalisée. Pour un système 50 Ω, cela correspond à Z = 25 + j50. S’il s’agit d’un circuit RL, alors R = 25 Ω et pour f = 800 MHz, le coefficient de self induction de la bobine serait :

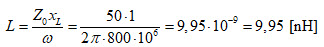
2^ème exemple : z = 1 + j2 en valeur normalisée. Pour un système 75 Ω, cela correspond à Z = 75 + j150. S’il s’agit d’un circuit RL, alors R = 75 Ω et pour f = 300 MHz, le coefficient de self induction de la bobine serait :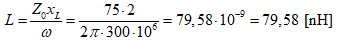

Un troisième réseau de cercles existe sur l’abaque de Smith. Celui-ci est implicite car les cercles ne sont pas tracés sur l’abaque mais ils peuvent être facilement construits et tracés au compas lors du calcul d’un circuit ou d’une ligne de transmission. Il s’agit des cercles à rapport d’ondes stationnaires constant (à SWR constant). Les cercles sont concentriques et ont tous pour centre celui de l’abaque. Comme le SWR est plus grand ou égal à l’unité, le rayon d’un cercle à SWR constant aura pour valeur celle des graduations du demi-axe X partant du centre de l’abaque (valeur 1:1) vers la droite jusqu’à la valeur ∞:1. La lecture s’effectue donc sur l’axe des résistances pures. La valeur lue au point d’intersection d’un cercle à SWR constant sur la partie de gauche de l’axe X correspond à l’inverse de la valeur lue sur le point d’intersection situé sur la partie de droite de l’axe.

Toutes les impédances complexes qui sont situées sur le cercle à SWR constant donneront le même rapport d’ondes stationnaires si ces impédances constituaient différentes charge au bout d’une ligne de transmission d’impédance caractéristique Z₀. Ce SWR reste aussi constant tout le long de la ligne de transmission (dans le cas de figure où la ligne est idéale, c’est-à-dire sans perte).

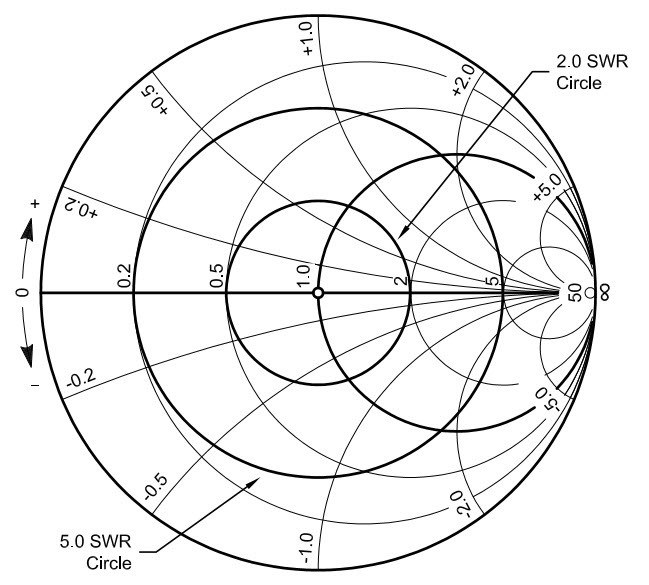
Fig. 11 : Tracé des cercles à SWR constant sur l’abaque de Smith. Source ARRL Antenna Book 21^st Edition.

Pour une charge d’une impédance donnée raccordée en fin de ligne de transmission, nous obtenons un SWR donné. Au fur et à mesure que l’on se déplace le long de la ligne, le SWR reste constant, mais l’impédance change en fonction du déplacement. L’impédance est donc lue sur le cercle à SWR constant. Le déplacement en fraction de longueur d’onde le long de la ligne de transmission est lu sur une des deux échelles situées sur le périmètre de l’abaque. Il suffit de tracer une droite partant du centre et passant par les coordonnées de l’impédance située sur le cercle à SWR constant. Les deux échelles sur le périmètre démarrent à la valeur zéro sur la gauche de l’abaque. La première est lue dans le sens antihorlogique pour un déplacement à partir de la source et qui progresse vers la charge (Toward Load). La deuxième est lue dans le sens horlogique pour un déplacement à partir de la charge et qui progresse vers la source (Toward Generator). Un tour complet sur le périmètre de l’abaque correspond à une demi-longueur d’onde (λ/2). Comme la valeur de l’impédance se répète tous le λ/2, le long d’une ligne de transmission, l’abaque peut être utilisé pour n’importe quelle longueur du moment où l’on y soustrait un multiple entier de λ/2 ; la longueur restante est celle qui est reportée sur l’abaque.

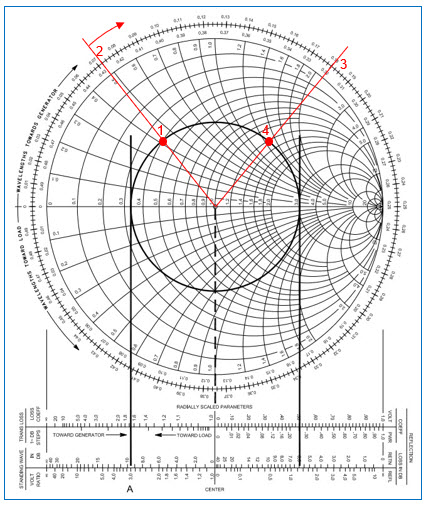
Fig. 12 : Déplacement vers la source le long d’une ligne de transmission où réside un SWR de 3:1. Le SWR est reporté en A sur l’échelle au bas de l’abaque. La charge a une impédance normalisée de 0,40+j0,42 (1); le déplacement va de 0,072λ (2) à 0,18λ (3), soit une longueur de ligne de 0,18‑0,072 = 0,108λ. L’impédance normalisée vue par la source est de 1,2+j1,25 (4). Source ARRL Antenna Book 21^st Edition.

Comment un Antenna Tuner doit-il adapter l’impédance d’une antenne à un émetteur ?

Soit une antenne ondes courtes d’une impédance qui a une partie résistive de 25 Ω et qui présente une réactance inductive de 25 Ω. La ligne de transmission raccordée à l’antenne est un câble coaxial RG213U d’impédance caractéristique de 50 Ω et dont la longueur est de 12,70 m. La fréquence de travail est de 51,450 MHz dans la bande des 6 m. Quelle sera l’impédance présente à la sortie de la boîte d’accord (Antenna Tuner) placée près de la station d’émission, c’est-à-dire quelle sera l’impédance vue à l’entrée de la ligne de transmission ?

Tout d’abord, que représente en longueur d’onde un câble RG213U de 12,70 m de long à une fréquence de 51,450 MHz ?

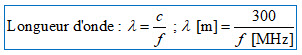
Mais la vitesse de propagation des ondes est plus lente dans un câble coaxial constitué d’un diélectrique autre que l’air sec (ou le vide) : il y a un facteur de vélocité du câble (VF, Velocity Factor, parfois noté v_f) qui relie sa longueur d’onde électrique à la longueur d’onde dans le vide (effet de raccourcissement).

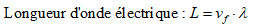
Pour un câble coaxial RG213U, le facteur de vélocité est de 0,66 ; d’où on peut calculer le nombre de longueurs d’onde électrique :

En soustrayant un nombre entier de λ/2 du nombre de longueurs d’onde, il reste 0,3λ.
L’impédance normalisée de l’antenne (charge, Load) est :

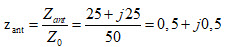
Cette impédance normalisée est située sur l’abaque à l’intersection du cercle à résistance constante de 0,5 et du cercle à réactance constante de +j0,5 (voir figure 11 au point « Load » 0,5+j0,5). On trace un cercle à SWR constant qui passe par le point d’impédance normalisée 0,5+j0,5. Le cercle intercepte la partie droite de l’axe X au point 2,62. Pour obtenir le résultat du SWR avec précision, on reporte avec le compas le rayon du cercle à SWR constant sur l’échelle située en dessous de l’abaque entre la ligne du centre et le point (A). La lecture au point (B) donne immédiatement la valeur du rapport d’ondes stationnaires en dB, soit 8,4 dB = 20 Log 2,62 (voir figure 13).

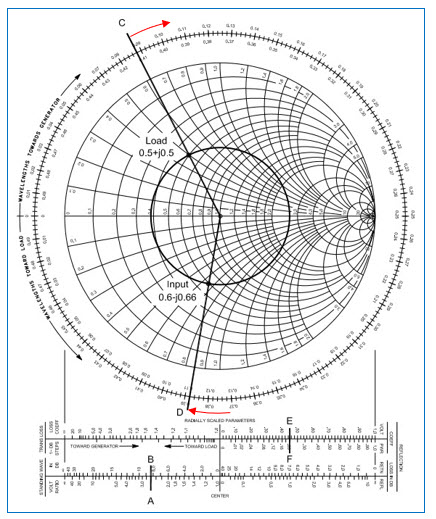
Fig. 13 : Calcul de l’impédance vue en début de ligne de transmission lorsqu’une antenne d’une impédance donnée est placée en fin de ligne d’une longueur physique donnée et pour une fréquence de travail donnée. Source ARRL Antenna Book 21^st Edition.

Ensuite on trace une droite partant du centre de l’abaque et passant par le point d’impédance de l’antenne. On peut lire sur le périmètre de l’abaque et sur l’échelle des longueurs d’onde « vers la source » (Toward Generator) une valeur de 0,088λ au point (C). Comme la longueur d’onde électrique de la ligne est de 0,3λ (à n fois λ/2 près), on va se déplacer dans le sens horlogique sur l’échelle périphérique de longueur d’onde d’une quantité de 0,3λ pour arriver au point (D) : 0,088λ+0,3λ = 0,388λ. Entre le point (D) et le centre de l’abaque, on trace une droite qui intercepte le cercle à SWR constant. Le point d’intersection de cette droite avec le cercle à SWR constant nous donne l’impédance normalisée qui apparaît en début (entrée) de ligne à la sortie de l’Antenna Tuner au point « Input »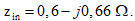
Pour obtenir l’impédance en entrée de ligne, on multiplie le résultat par l’impédance caractéristique de la ligne de transmission :
qui représente une partie résistive de 30 Ω et une réactance capacitive de 33 Ω. C’est cette impédance-là que l’Antenna Tuner va devoir adapter à la sortie de l’émetteur. L’impédance en début de ligne est complètement différente de celle de l’antenne en sortie de ligne. C’est bon à savoir !

En reportant avec un compas la longueur du rayon du cercle à SWR constant sur l’échelle SWR située en dessous de l’abaque, on peut trouver le coefficient de réflexion en tension au point (E) qui nous donne une valeur de 0,45. Cela signifie que 45 % de la tension de l’onde incidente est réfléchie. Sur la même échelle et sur les graduations qui se trouvent juste en dessous, on peut trouver le coefficient de réflexion en puissance au point (F) qui nous donne une valeur de 0,20. Cela signifie que 20 % de la puissance de l’onde incidente est réfléchie. La valeur en puissance est proportionnelle au carré de la tension : (0,45)² = 0,2

Il faut bien comprendre ce que nous venons de faire sur l’abaque de Smith : il s’agit d’un déplacement sur la circonférence du cercle à SWR constant où nous pouvons lire le changement d’impédance présent dans la ligne de transmission au fur et à mesure du déplacement dans cette ligne à partir de la charge dans la direction de la source. En pratique, cela signifie que si l’on mesure le rapport d’ondes stationnaires dans la ligne de transmission au moyen d’un wattmètre – ROS-mètre, l’appareil de mesure nous donnera toujours la même mesure de ROS quel que soit l’endroit le long de la ligne où l’on place l’appareil de mesure (pour une ligne idéale sans pertes). En revanche, si on veut effectuer une mesure d’impédance présente dans la ligne de transmission avec un pont de mesure d’impédance, l’appareil de mesure nous donnera une mesure différente à chaque déplacement le long de la ligne. Ceci est résumé graphiquement à la figure suivante.

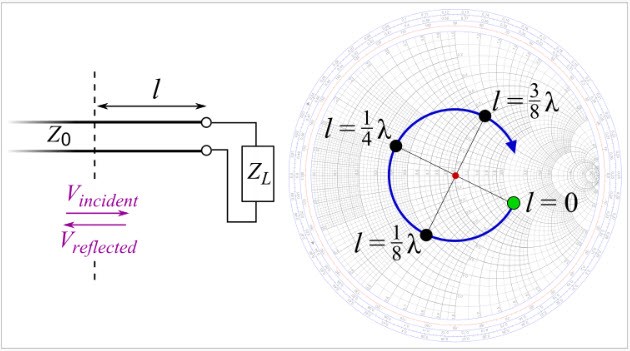
Fig. 14 : Changement de l’impédance dans une ligne de transmission lors d’un déplacement d’une longueur l de la charge vers la source. Le SWR reste constant tout le long de la ligne. La ligne est supposée idéale sans perte. Source : Wikipedia Smith Chart.

Coordonnées en impédance et en admittance :

Lorsqu’un réseau est composé d’impédances en série, les impédances s’additionnent ; en revanche lorsque le réseau est composé d’impédances en parallèle, il faut additionner les inverses des impédances pour obtenir l’inverse de l’impédance équivalente. Comme l’admittance est l’inverse d’une impédance, le calcul est plus facile pour des impédances en parallèle, il suffit d’additionner les admittances. Il en est de même pour les résistances, les réactances, les conductances et les susceptances. L’abaque de Smith permet d’effectuer directement la conversion d’une impédance en admittance et vice-versa.

Pour effectuer la conversion d’une impédance en admittance sur l’abaque, il suffit de prendre les coordonnées diamétralement opposées sur un cercle à SWR constant. Tous les diamètres des cercles à SWR constant passent par le centre de l’abaque.

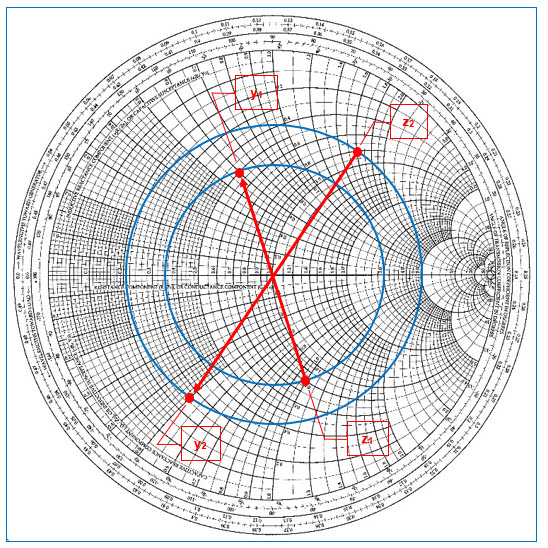
Fig. 15 : Conversion d’impédances en admittances. z₁ = 0,8-j1 donne y₁ = 0,49+j0,61 et
z₂ = 0,8+j1,6 donne y₂ = 0,25-j0,5. Il y a lieu de se rappeler lors de la conversion Impédance–Admittance qu’une capacitance (réactance négative) est considérée comme une susceptance positive et qu’une inductance (réactance positive) est considérée comme une susceptance négative. Graphisme : ON4IJ.

Comment déterminer l’impédance d’une antenne lorsqu’on se trouve à distance et à l’entrée de la ligne de transmission du côté de la station d’émission ?

La résolution du calcul par l’abaque de Smith s’effectue dans le chemin inverse de ce que nous avons réalisés à la figure 13. Voir l’exemple ci-dessous.
Prenons l’exemple chiffré suivant : avec un pont de mesure d’impédance (ou un Antenna Analyzer), on effectue une lecture d’une impédance de 70 Ω - j25 Ω à l’entrée de la ligne coaxiale de 50 Ω. La longueur d’onde électrique de la ligne coaxiale a été mesurée à la fréquence de travail et a pour valeur 2,35λ. Quelle est l’impédance de l’antenne ?
L’impédance normalisée de celle qui a été mesurée à l’entrée de la ligne 50 Ω est : 70/50-j25/50 = 1,4-j0,5. Plaçons cette impédance en coordonnées sur l’abaque et traçons un cercle à SWR constant passant par ce point « Input » (entrée de la ligne). En reportant le rayon du cercle à SWR constant sur l’échelle SWR (Voltage Ratio) située en dessous de l’abaque, on trouve au point (A) un SWR de 1,7:1 (voir figure 16).
Traçons une droite à partir du centre de l’abaque et passant par le point d’impédance « Input » jusqu’à l’échelle des longueurs d’onde située au périmètre de l’abaque. Comme on effectue un déplacement depuis l’entrée de la ligne (là-où nous avons effectué la mesure d’impédance) vers l’antenne qui est la charge, on doit lire la graduation sur l’échelle des longueurs d’ondes vers la charge (Toward Load). La lecture au point (B) nous donne une valeur de référence 0,195λ. Sur cette échelle de longueurs d’onde, on va se déplacer dans le sens antihorlogique de la valeur de la longueur d’onde électrique du câble coaxial, c’est-à-dire de 2,35λ à partir de la valeur de référence de 0,195λ, ce qui donne 0,195λ + 2,35λ = 2,545λ. Comme cette longueur d’onde est plus grande que λ/2, on va y soustraire un nombre entier de λ/2 : 2,545λ‑(5xλ/2) = 0,045λ qui se situe au point (C).
Traçons une droite partant du centre de l’abaque et passant par le point (C) à la graduation de 0,045λ. Cette droite intercepte le cercle à SWR constant aux coordonnées d’impédance de la charge au point « Load (Antenna) » où on peut lire une impédance normalisée de 0,62-j0,19. Pour trouver l’impédance de l’antenne on doit multiplier l’impédance normalisée par 50 Ω, ce qui donne 31 Ω - j9,5 Ω, c’est-à-dire une impédance composée d’une partie résistive de 31 Ω et d’une réactance capacitive de 9,5 Ω à la fréquence de travail.

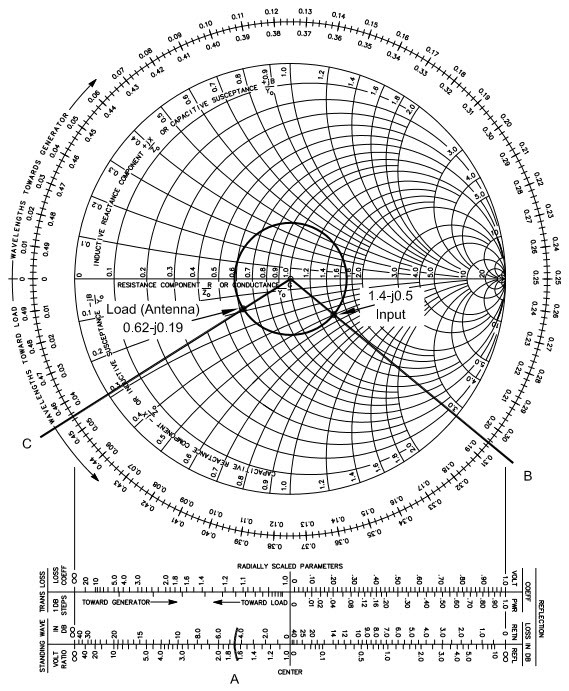
Fig. 16 : Calcul de l’impédance d’une antenne à partir d’une mesure d’impédance effectuée à l’entrée d’une ligne de transmission d’une longueur de 2,35λ. Le texte d’explication se situe à la page précédente. Source ARRL Antenna Book 21^st Edition.

Comment déterminer l’impédance d’une antenne sans pont de mesure d’impédance mais uniquement avec un wattmètre – ROS-mètre ?

Prenons un cas pratique avec quelques chiffres. Soit une antenne verticale du type Ground Plane qui est parfaitement taillée à λ/4 et est donc pile à la résonnance sur la fréquence de travail. Cette antenne est alimentée par un câble coaxial (idéal sans perte) de 50 Ω dont la longueur d’onde électrique mesurée à la fréquence de travail est de 0,95λ. Un wattmètre – ROS-mètre (avec coupleur directionnel intégré) est placé au début de la ligne de transmission. La lecture du ROS (SWR) sur l’appareil donne une valeur de 1,7:1. Nous voulons chercher l’impédance de l’antenne et celle qui sera présente au début de la ligne de transmission.

Nous ne pouvons pas placer un point d’impédance normalisée donnée sur l’abaque. Toutefois, comme le SWR ne varie pas le long de la ligne de transmission, le SWR mesuré en début de ligne est le même que celui qui est présent aux bornes de l’antenne (dans le cas d’une ligne idéale sans perte). Traçons un cercle à SWR constant de 1,7:1 sur l’abaque de Smith (voir figure 17).

Comme l’antenne est parfaitement à la résonnance à la fréquence de travail, celle-ci offre une impédance résistive pure sans partie réactive. Sur l’abaque, une résistance pure se situe sur l’axe horizontal X. Le cercle à SWR constant de 1,7:1 intercepte l’axe X à deux endroits : sur la partie droite à une valeur de 1,7 et sur la partie gauche à une valeur inverse de 1,7, c’est-à-dire à une valeur de 0,59. Lorsque l’antenne est à la résonnance et qu’elle présente un ROS de 1,7:1 sur une ligne de transmission de 50 Ω, alors il y a deux points d’impédances normalisées qui satisfont à la condition de résonnance : 0,59+j0 et 1,7+j0. Ces impédances normalisées, une fois multipliées par 50 Ω donnent les impédances suivantes : 0,59 x 50 = 29,5 Ω c’est-à-dire une résistance pure de 29,5 Ω et de 1,7 x 50 = 85 Ω, c’est-à-dire une résistance pure de 85 Ω.

Comme il s’agit d’une antenne Ground Plane quart d’onde, l’impédance théorique de ce type d’antenne est proche de 36 Ω. Parmi les deux valeurs trouvées ci-dessus, on peut raisonnablement écarter la valeur de 85 Ω au profit de la valeur de 29,5 Ω et c’est cette valeur qui sera retenue pour les calculs qui suivent sur l’abaque de Smith.

La valeur de l’impédance normalisée de l’antenne étant donc de 0,59+j0 sur le cercle à SWR constant de 1,7:1 nous allons pouvoir calculer l’impédance à l’entrée de la ligne coaxiale de 50 Ω et ayant pour longueur d’onde électrique une valeur de 0,95λ. En soustrayant 1 x λ/2 de cette valeur, il reste un déplacement de longueur d’onde de ligne de transmission de 0,95λ-0,5λ = 0,45λ. Comme nous partons de l’impédance de l’antenne et que l’on remonte vers la source, nous allons nous déplacer sur l’échelle des longueurs d’onde sur le périmètre de l’abaque dans le sens horlogique (Toward Generator). La longueur d’onde de départ est zéro car on se situe sur la partie gauche de l’axe X de l’abaque. Après un déplacement de 0,45λ, on trouve une valeur de 0,63‑j0,20. L’impédance vue à l’entrée de la ligne de transmission sera donc de : (0,63 x 50)‑j(0,20 x 50) = 31,5-j10 Ω. On constate en début de ligne que la partie résistive devient 31,5 Ω, mais qu’il y a à présent une partie réactive capacitive d’une réactance de 10 Ω bien que l’antenne soit à la résonnance. C’est bon à savoir.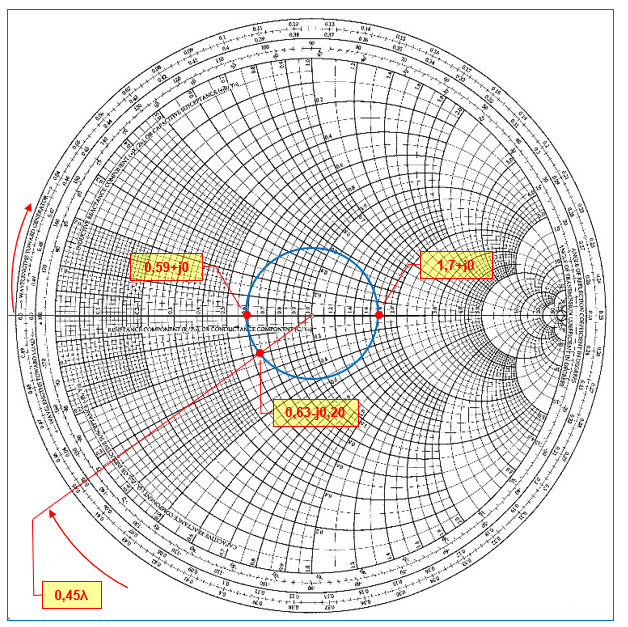

Fig. 17 : Calcul de l’impédance d’une antenne Ground Plane quart d’onde parfaitement à la résonnance et qui présente un ROS de 1,7:1. Calcul de l’impédance vue en début de ligne coaxiale de 50 Ω et d’une longueur d’onde électrique de 0,95λ sur la fréquence de résonnance de l’antenne. Le texte d’explication se situe à la page précédente. Graphisme : ON4IJ.

Dans les exemples calculés ci-dessus, nous avons toujours supposé que la ligne de transmission était idéale, c’est-à-dire sans perte. Dans le monde réel, toutes les lignes de transmission ont une atténuation linéique donnée en décibel par unité de longueur et en fonction de la fréquence de travail. Pour un Feeder d’antenne l’atténuation peut devenir conséquente, en particulier pour des lignes à fortes pertes, pour des grandes longueurs ou à des fréquences élevées spécialement en VHF, UHF et SHF.
L’atténuation d’une ligne de transmission a pour conséquence de faire varier le rapport d’ondes stationnaires le long de cette ligne. Le SWR décroît lorsque l’on s’écarte de la charge en direction vers la source. En ce qui concerne les cercles à SWR constant sur l’abaque de Smith, ceux-ci devraient prendre la forme d’une spirale rentrante vers le centre et tracée dans le sens horlogique (vers la source) à partir du point où se situe l’impédance normalisée de la charge (voir figure 18). La progression de la spirale vers le centre est fonction de l’atténuation linéique de la ligne.

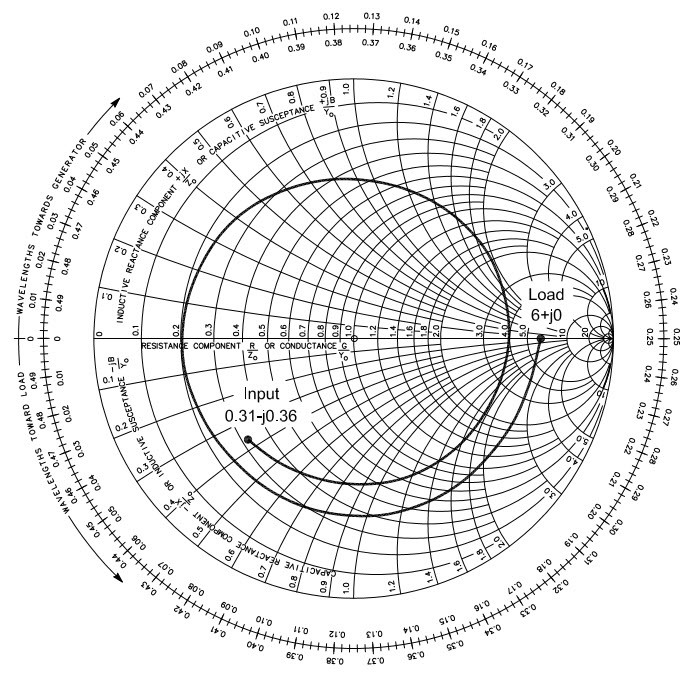
Fig. 18 : Cercle à SWR constant devenant une spirale lorsqu’on tient compte des pertes linéiques de la ligne de transmission. Cet exemple illustre une antenne de 300 Ω parfaitement à la résonnance sur une fréquence de 28 MHz alimentée par un câble coaxial RG174U de 4,88 m de long, d’impédance caractéristique de 50 Ω, de facteur de vélocité de 0,66 et d’une atténuation de 20,34 dB par 100 m à 28 MHz. Le ROS aux bornes de l’antenne est de 6:1 mais celui-ci atteint la valeur de 3,6:1 à l’entrée de la ligne du côté de l’émetteur. En pratique, on ne trace pas la spirale mais bien deux cercles concentriques dont le premier est un cercle à SWR constant (le SWR à l’antenne) et le deuxième est un cercle à SWR constant (à l’entrée de la ligne) dont la valeur du SWR est calculée en fonction de l’atténuation totale de la ligne entre l’émetteur et l’antenne. Source ARRL Antenna Book 21^st Edition.

Lorsque je mesure un ROS à la sortie de l’émetteur, quel sera le ROS à l’antenne si j’ai une longue ligne de transmission qui présente des pertes ?

Prenons le cas d’une ligne de transmission qui présente -3 dB de pertes à la fréquence de travail sur toute la longueur du Feeder entre un émetteur et une antenne. Un wattmètre – ROS-mètre est placé entre la sortie de l’émetteur et l’entrée de la ligne de transmission. La lecture du ROS sur l’appareil de mesure nous donne une valeur de 1,7:1. Quelle lecture aurait donné l’appareil s’il avait été placé tout en haut directement à l’antenne ?

Sur l’abaque de Smith, traçons un premier cercle à SWR constant de rayon 1,7 (voir figure 19) ; la longueur du rayon peut être trouvée sur l’échelle radiale SWR (partie de gauche) située en dessous de l’abaque (voir figure 20). Ensuite, on reporte avec un compas la longueur de ce rayon sur l’échelle radiale « ATTEN. [dB] » (partie de droite), (voir figure 21). Cette échelle est parfois appelée « 1 dB Step » (saut de 1 dB) car c’est sur cette échelle que l’on reporte l’atténuation avec un « saut » d’atténuation. Il y a lieu de bien remarquer que les graduations ne sont pas régulièrement espacées : pour des SWR de faibles valeurs (rayons courts), un saut de 1 dB modifie peu la longueur du rayon du deuxième cercle à SWR constant ; en revanche, pour des SWR de valeurs élevées, un saut de 1 dB va beaucoup modifier la longueur du rayon du deuxième cercle à SWR constant.

Lorsque la longueur du rayon du cercle à SWR constant de 1,7 est reportée sur l’échelle d’atténuation de la ligne de transmission (ATTEN. [dB]), on arrive à une graduation de 5,9 dB (figure 21) ; cette valeur est une valeur relative et non pas une valeur absolue. Comme le ROS de 1,7:1 a été mesuré au départ de la source, c’est vers la charge que le déplacement va avoir lieu dans la ligne de transmission pour obtenir le ROS aux bornes de l’antenne. Le saut de 3 dB de perte de notre ligne de transmission va donc être effectué selon le sens de la flèche « Toward Load » qui est indiqué sur l’échelle d’atténuation. Pour effectuer un saut de 3 dB à partir de la graduation 5,9 dB en direction de la charge, on doit arriver à la graduation 2,9 dB (figure 21), (5,9-2,9 = 3 dB). On remarque que le saut de 3 dB dans ce cas-ci abouti à une augmentation de la longueur du rayon pour le deuxième cercle à SWR constant.

Au moyen d’un compas, nous allons relever la nouvelle longueur et reporter celle-ci à nouveau sur l’échelle radiale SWR (partie gauche), (voir figure 20). Sur l’échelle SWR, la nouvelle longueur arrive à la graduation de 3,18. Le ROS à l’antenne sera donc de 3,18:1. On constate que la valeur du ROS de 1,7:1 du côté de l’émetteur donne en réalité un ROS de 3,18:1 à l’antenne. C’est donc à cause de la perte de 3 dB de la ligne de transmission que nous mesurons un ROS de 1,7:1 à l’émetteur alors qu’en réalité, il est de 3,18:1 à l’antenne. Bon à savoir !

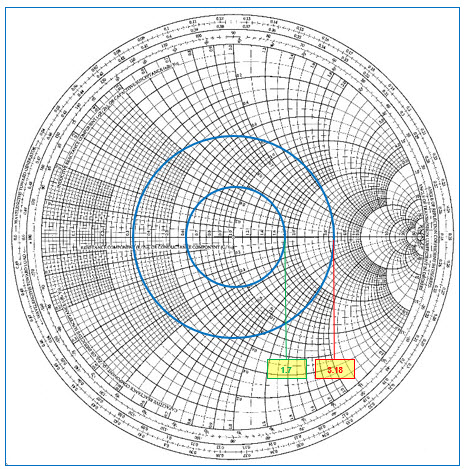
Fig. 19 : Cercles à SWR constant de 1,7:1 en entrée de ligne du côté de l’émetteur. Après une ligne présentant une perte de -3 dB, le SWR atteint une valeur 3,18:1 au niveau de l’antenne. Bon à savoir.

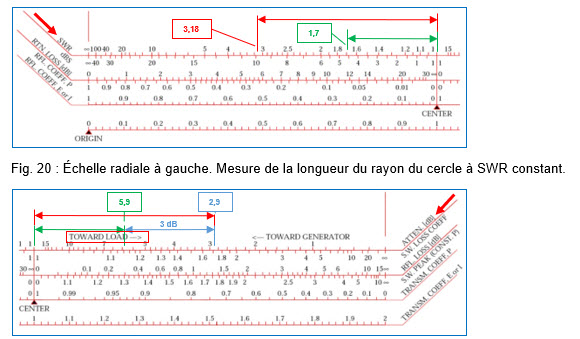
Fig. 21 : Échelle radiale à droite : « 1 dB Step » (Atten. [dB]) pour reporter l’atténuation (par sauts de 1 dB) de la ligne de transmission. La longueur du rayon du 1^er cercle SWR 1,7 arrive à la graduation 5,9 dB. Saut de 3 dB vers la charge (Toward Load), on arrive à la graduation 2,9. La longueur totale devient celle du rayon du 2^ème cercle SWR reporté sur l’échelle SWR 3,18 à la figure précédente.

Dans ce que nous venons d’observer ci-dessus, les calculs effectués sur l’abaque de Smith en tenant compte de la perte de la ligne de transmission nous conduisent à tracer deux cercles à SWR constant. Si l’on doit calculer l’impédance de l’antenne, celle-ci sera située sur le cercle extérieur (SWR 3,18:1). Si l’on doit calculer l’impédance vue à l’entrée de la ligne de transmission, celle-ci sera située sur le cercle intérieur (SWR 1,7:1). Selon les publications d’abaques de Smith, l’échelle radiale « 1 dB Step » (Atten. [dB]) peut parfois être présente sur la partie gauche de l’échelle radiale à la place de la partie droite. Cette échelle peut parfois être graduée sans valeur annotée en face des graduations car un saut de 1 dB est un écart purement relatif. Pour un saut de plusieurs dB, il suffit de compter le nombre de graduations correspondant à la valeur du saut d’atténuation à effectuer.
L’exemple ci-dessous illustre le calcul du SWR à l’entrée et à la sortie de ligne, et aussi le calcul de l’impédance en sortie de ligne pour une mesure donnée d’impédance vue à l’entrée de la ligne.

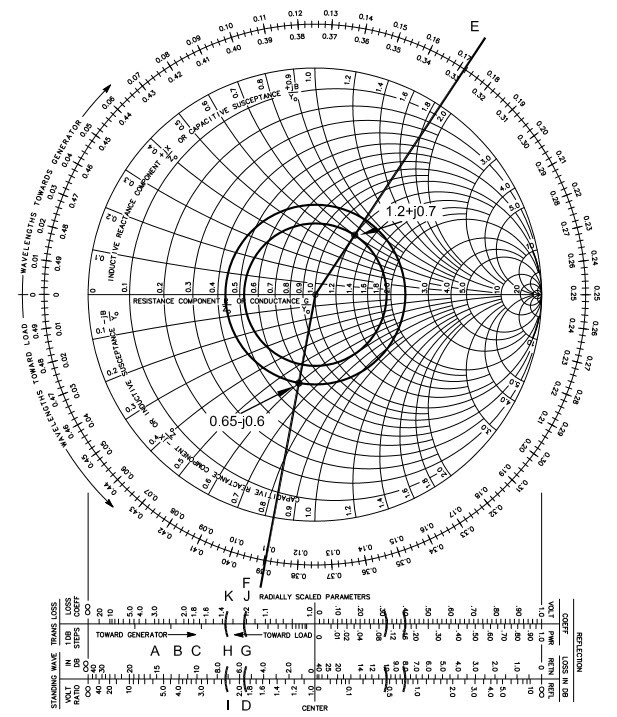
Fig. 22 : Calcul de SWR et d’impédances tenant compte d’une atténuation de ligne de 1 dB, d’une longueur de 0,282λ et d’impédance de 50 Ω. L’impédance mesurée à l’entrée de la ligne est Z=60+j35 Ω et donc z=1,2+j0,7. Le SWR calculé à l’entrée (émetteur) est de 1,9:1 et celui de la sortie (antenne) donne une valeur calculée de 2,3:1. L’impédance de la charge donne une valeur calculée de z=0,65‑j0,6 et donc Z=32,5-j30 Ω. L’échelle radiale 1 dB Step est située sur la gauche. Source ARRL Antenna Book 21^st Edition.
Nous commençons à apprivoiser l’abaque de Smith et son aspect mystérieux commence à s’éclaircir ; c’est un bon début. Allons, courage ! Le plus beau vient dans la suite.
Maintenant que nous sommes capables de déterminer quelle est l’impédance complexe qui est présente à l’entrée d’une ligne de transmission lorsque la sortie de celle-ci est chargée par une antenne, le défi qui reste à relever est celui du calcul d’un réseau d’adaptation d’impédance. Cela nous sera bien utile pour déterminer les composants d’un Antenna Tuner ou de tout autre réseau adaptateur d’impédance.
Question simple : pourquoi un circuit d’adaptation est-il composé uniquement de réactances pures telles des capacitances (condensateurs) et des inductances (bobines d’induction) et qu’il n’y a aucune résistance ?
Réponse simple : une réactance pure ne consomme aucune énergie sur le trajet du signal. En effet, toute l’énergie qui a été emmagasinée dans le composant lors d’une alternance du signal est restituée lors de l’alternance opposée qui suit immédiatement. Pour s’en convaincre, on peut facilement le vérifier sur un oscilloscope numérique en activant une fonction mathématique de multiplication entre deux canaux auxquels on injecte deux sinusoïdes en quadrature de phase (à 90° de phase). La première sinusoïde représentant une tension, la deuxième un courant, la multiplication représente une puissance (ou une énergie par unité de temps). Lorsque les deux sinusoïdes sont en quadrature de phase (avance ou retard de 90°), la valeur moyenne des deux sinusoïdes multipliées donne une valeur zéro. La puissance absorbée lors d’une alternance est totalement restituée lors de l’alternance suivante. En revanche, lorsque deux sinusoïdes sont parfaitement en phase, comme c’est le cas de la tension et du courant dans une résistance pure, la valeur moyenne des deux sinusoïdes multipliées se trouve à son maximum. Le signal obtenu par la multiplication est strictement positif pour deux sinusoïdes en phases. Ceci signifie que l’absorption d’énergie est maximale et qu’il n’y a aucune restitution d’énergie : tout et dissipé (en chaleur) dans la résistance. Voilà pourquoi les réseaux adaptateurs d’impédance sont constitués uniquement de réactance. Il y a une seule exception : il s’agit des adaptateurs purement résistifs à large bande et à atténuation minimale (MLP, Minimum Loss Pad) souvent utilisés pour une adaptation d’impédance entre 75 Ω et 50 Ω et vice-versa. Toutefois, ces atténuateurs sont uniquement utilisés pour des signaux à faible puissance dans le domaine de la mesure.

Avant d’aborder la suite, nous allons résumer les quatre chemins de base parcourus sur l’abaque de Smith lorsqu’on place des réactances en série ou en parallèle dans un réseau adaptateur d’impédance.
Lorsqu’on place un point représentant une impédance complexe sur l’abaque de Smith, celui-ci se situe à l’intersection d’un cercle à résistance constante et d’un cercle à réactance constante (réseaux des cercles d’impédance de l’abaque). Si on déplace ce point le long d’un cercle à résistance constante, cela revient à introduire une réactance car on croise une série de cercles de différentes réactances. Il en est de même sur les deux réseaux des cercles miroités d’admittance de l’abaque lorsqu’on se déplace sur un cercle à conductance constante : on croise une série de cercle de différentes susceptances. Voir la figure 5 qui illustre les réseaux des cercles d’impédance et d’admittance (imittance).
Selon les sens de déplacement sur un cercle à résistance constante, on introduit une composante d’inductance ou de capacitance en série dans le circuit électronique du réseau ; de même, sur un cercle à conductance constante, on introduit une susceptance inductive ou capacitive en parallèle dans le circuit électronique du réseau.
La valeur de la réactance ou de la susceptance introduite dans le réseau correspond à l’amplitude du déplacement le long du cercle à résistance ou à conductance constante.
Prenons les quatre possibilités :

Du point d’impédance normalisée z₁=0,4+j0,2 on se déplace dans le sens horlogique vers le point z₂=0,4+j0,5 : cela revient à introduire une réactance série de +j0,5-(+j0,2) = +j0,3, c’est-à-dire une inductance de +j0,3 ;
Du point d’impédance normalisée z₃=0,4+j1 on se déplace dans le sens antihorlogique vers le point z₄=0,4+j0,5 : cela revient à introduire une réactance série de +j0,5-(+j1) = -j0,5, c’est-à-dire une capacitance de -j0,5 ;
Du point d’admittance normalisée y₅=0,4+j0,2 on se déplace dans le sens antihorlogique vers le point y₆=0,4-j0,4 : cela revient à introduire une susceptance (impédance parallèle) de -j0,4‑(+j0,2) = -j0,6, c’est-à-dire une susceptance inductive de -j0,6 ;
Du point d’admittance normalisée y₇=0,4+j1 on se déplace dans le sens horlogique vers le point y₈=0,4+j1,8 : cela revient à introduire une susceptance (impédance parallèle) de +j1,8‑(+j1) = +j0,8, c’est-à-dire une susceptance capacitive de +j0,8.

Ces quatre types de déplacement sont illustrés en résumé sur la figure ci-dessous.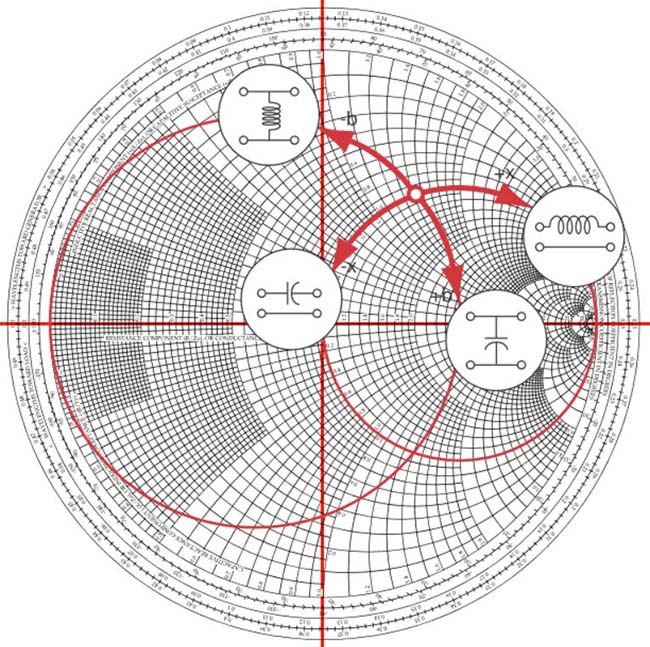

Fig. 23 : Un déplacement le long d’un cercle à résistance constante introduit une réactance série. Un déplacement le long d’un cercle à conductance constante introduit une susceptance (réactance parallèle). Selon le sens horlogique ou antihorlogique de déplacement, la réactance ou la susceptance est inductive ou capacitive. Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

Pour les quatre possibilités d’amplitude de déplacement sur l’abaque, on peut calculer la valeur du composant introduit (bobine d’induction, condensateur, composant placé en série ou en parallèle dans le réseau) en fonction de l’impédance du système (impédance caractéristique de la ligne de transmission) et en fonction de la fréquence de travail. C’est ici que nous allons profiter des formules de la page 7. Nous allons visualiser tout cela sur les quatre figures suivantes en prenant les quatre valeurs mentionnées à la page 27. Dans chaque exemple nous prendrons un système d’impédance de 50 Ω et une fréquence de travail de 1 GHz pour le calcul de la valeur des composants (bobine d’induction ou condensateur).

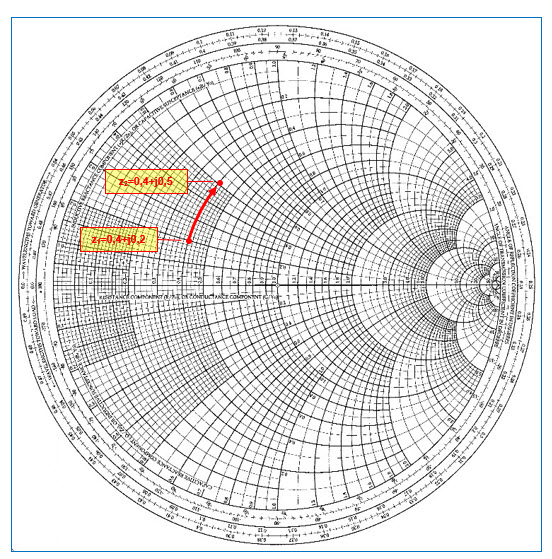
Fig. 24 : Déplacement sur un cercle à résistance constante dans le sens horlogique introduisant une inductance série. Z₀ = 50 Ω ; f = 1 GHz ; x_L = +j0,3. Graphisme : ON4IJ.

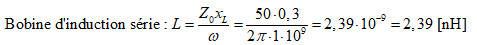
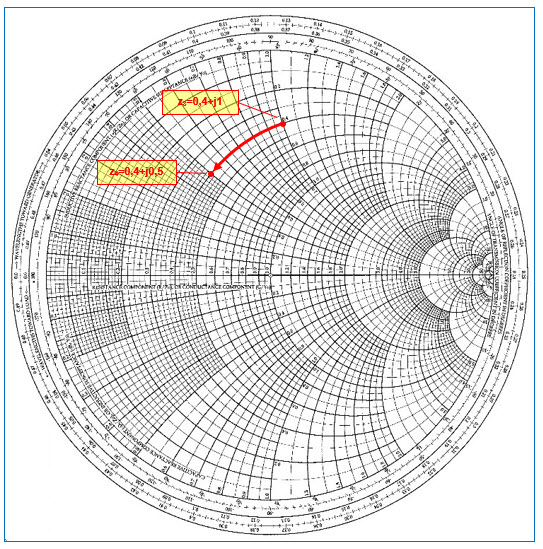
Fig. 25 : Déplacement sur un cercle à résistance constante dans le sens antihorlogique introduisant une capacitance série. Z₀ = 50 Ω ; f = 1 GHz ; x_C = -j0,5. Graphisme : ON4IJ.

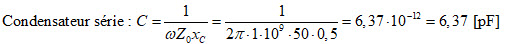
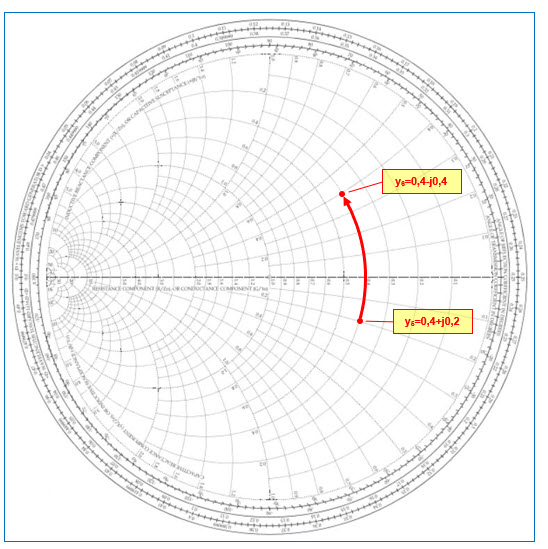
Fig. 26 : Déplacement sur un cercle à conductance constante dans le sens antihorlogique introduisant une inductance parallèle. Z₀ = 50 Ω ; f = 1 GHz ; b_L = -j0,6. Graphisme : ON4IJ.

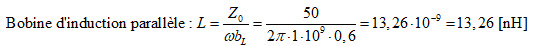
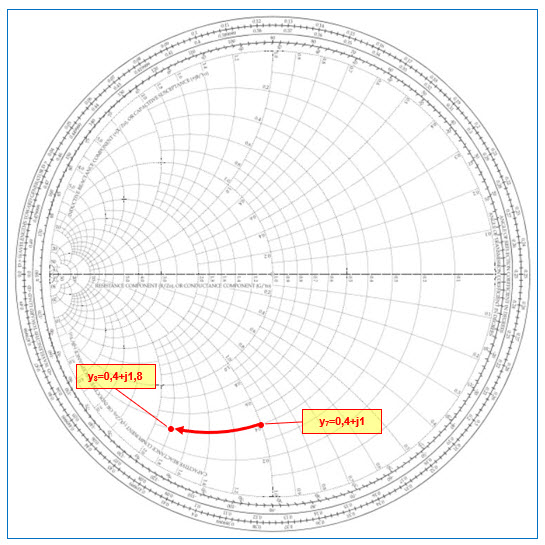
Fig. 27 : Déplacement sur un cercle à conductance constante dans le sens horlogique introduisant une capacitance parallèle. Z₀ = 50 Ω ; f = 1 GHz ; b_C = +j0,8. Graphisme : ON4IJ.

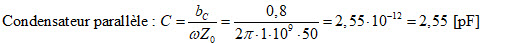
Comment constituer un réseau adaptateur d’impédance ?

Le réseau le plus simple permettant d’adapter n’importe quelle impédance à l’impédance caractéristique d’une ligne de transmission est le circuit en « L » car il permet de corriger aussi bien la partie réactive que la partie résistive de la charge à adapter. Le circuit en « L » est constitué de deux composants : un condensateur et une bobine d’induction dont un des composants est placé en parallèle sur l’entrée ou la sortie du réseau et dont l’autre composant est placé en série dans le circuit. Le circuit en « L » peut aussi être constitué de deux condensateurs (un en parallèle, l’autre en série) ou bien de deux bobines d’induction (une en parallèle et l’autre en série). Il y a donc huit possibilités d’agencement des circuits adaptateurs en « L ». Ces circuits sont encore appelés à « éléments localisées » (Lumped Elements) car il s’agit de réactances ponctuelle à un endroit déterminé du réseau contrairement aux circuits à éléments distribués comme c’est le cas le long d’une ligne de transmission ou dans les circuits d’adaptation par Stub (voir page 77).

Quel agencement et quels composants doit-on choisir pour un réseau en « L » ?

Le Yin et le Yang :

Sur l’abaque de Smith, en fonction de la situation du point représentant l’impédance à adapter, il y a plusieurs solutions possibles pour calculer un circuit mais il y a aussi plusieurs solutions incompatibles qu’il faut écarter. En fonction du type d’agencement du réseau en « L », il y a différentes « zones interdites » (Forbidden Area) sur l’abaque qui s’imbriquent selon une forme qui fait penser à la représentation symbolique du Yin et du Yang.

Fig. 28 : Représentation symbolique du Yin et du Yang évoquant la forme des zones interdites de l’abaque de Smith en fonction de l’agencement d’un réseau adaptateur d’impédance en « L ».
Le but d’un réseau adaptateur est de ramener l’impédance à adapter à la valeur de l’impédance caractéristique de la ligne de transmission se situant en impédance normalisée au centre de l’abaque. Les parcours sur l’abaque démarrent du composant placé du côté de la charge et se terminent au composant placé du côté de la source. Pour arriver au centre de l’abaque, il faut effectuer des déplacements le long d’un cercle à résistance ou à conductance constante jusqu’à ce que l’on rencontre un cercle de résistance ou de conductance unitaire. Dès qu’un cercle unitaire est atteint, le dernier déplacement s’effectue le long de ce cercle qui passe par le centre de l’abaque et le tour est joué.
Les figures suivantes illustrent les huit possibilités d’agencement des réseaux en « L ». Les figures reproduites ci-dessous sont extraites de l’exposé « Mysteries of the Smith Chart, Transmission Lines, Impedance matching and Little Known Facts » de Stephen D. Stearns K6OIK présenté à la Pacific Division Convention (Pacificon) de l’ARRL (American Radio Relay League) à Santa Clara, Californie, USA, qui a eu lieu du 14 au 16 Octobre 2001.

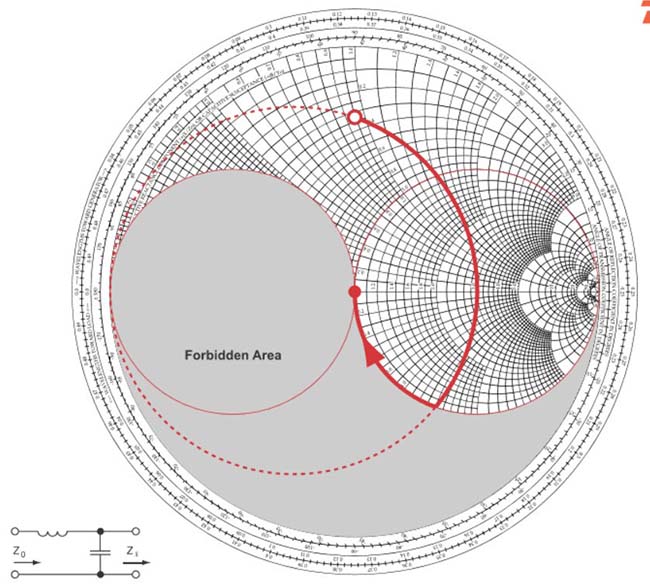
Fig. 29 : 1^er type de réseau adaptateur : condensateur parallèle (parcours en sens horlogique sur un cercle à conductance constante) et bobine d’induction série (parcours en sens horlogique sur un cercle à résistance constante). Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.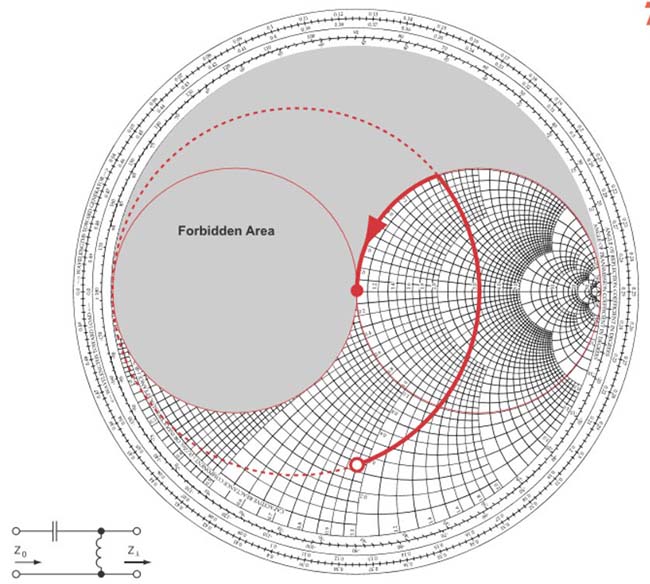

Fig. 30 : 2^ème type de réseau adaptateur : bobine d’induction parallèle (parcours en sens antihorlogique sur un cercle à conductance constante) et condensateur série (parcours en sens antihorlogique sur un cercle à résistance constante). Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

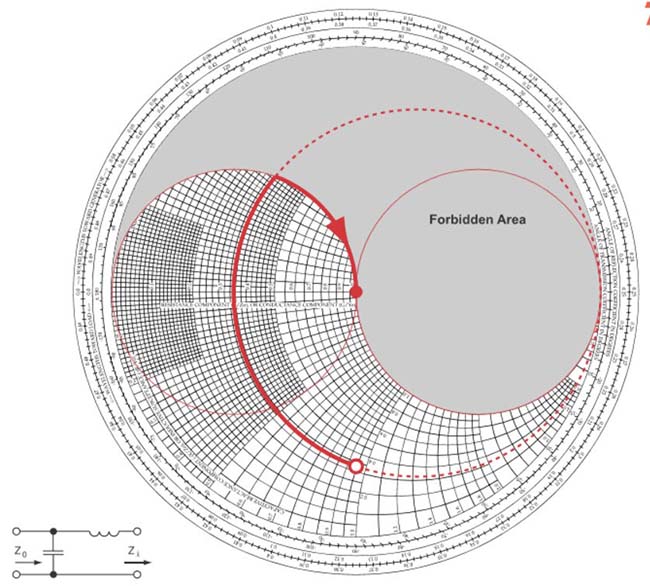
Fig. 31 : 3^ème type de réseau adaptateur : bobine d’induction série (parcours en sens horlogique sur un cercle à résistance constante) et condensateur parallèle (parcours en sens horlogique sur un cercle à conductance constante). Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

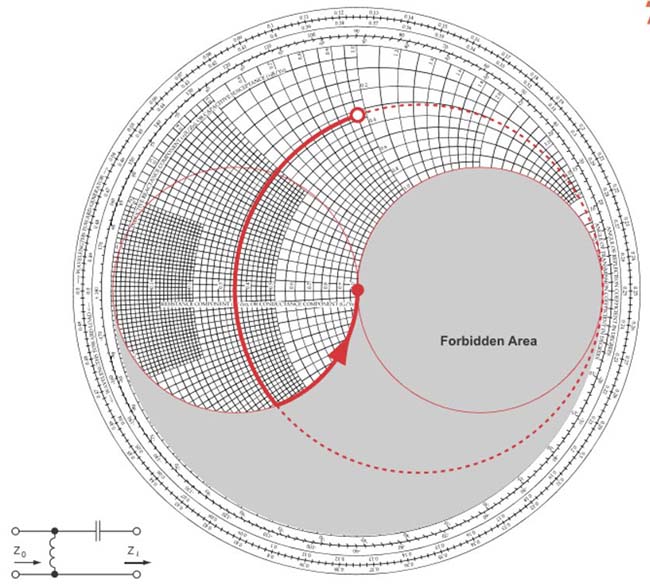
Fig. 32 : 4^ème type de réseau adaptateur : condensateur série (parcours en sens antihorlogique sur un cercle à résistance constante) et bobine d’induction parallèle (parcours en sens antihorlogique sur un cercle à conductance constante). Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

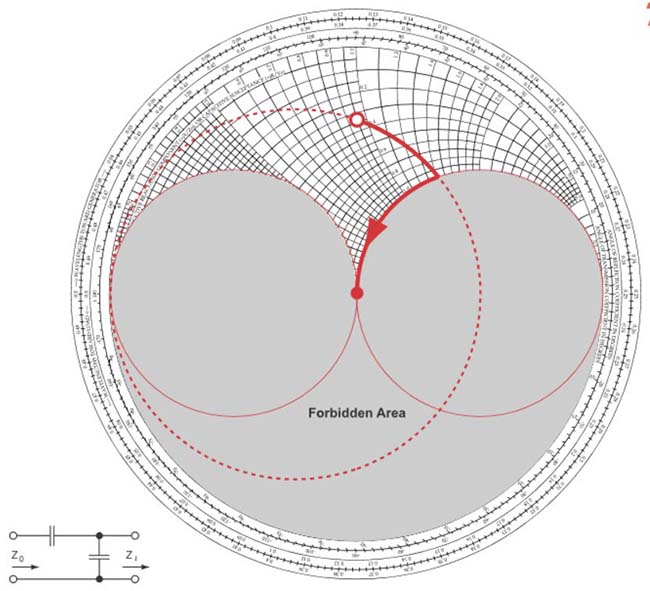
Fig. 33 : 5^ème type de réseau adaptateur : condensateur parallèle (parcours en sens horlogique sur un cercle à conductance constante) et condensateur série (parcours en sens antihorlogique sur un cercle à résistance constante). Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

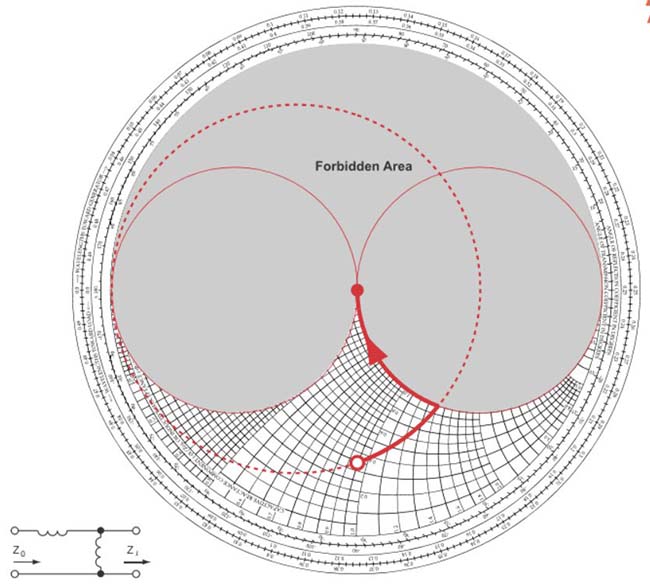
Fig. 34 : 6^ème type de réseau adaptateur : bobine d’induction parallèle (parcours en sens antihorlogique sur un cercle à conductance constante) et bobine d’induction série (parcours en sens horlogique sur un cercle à résistance constante). Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

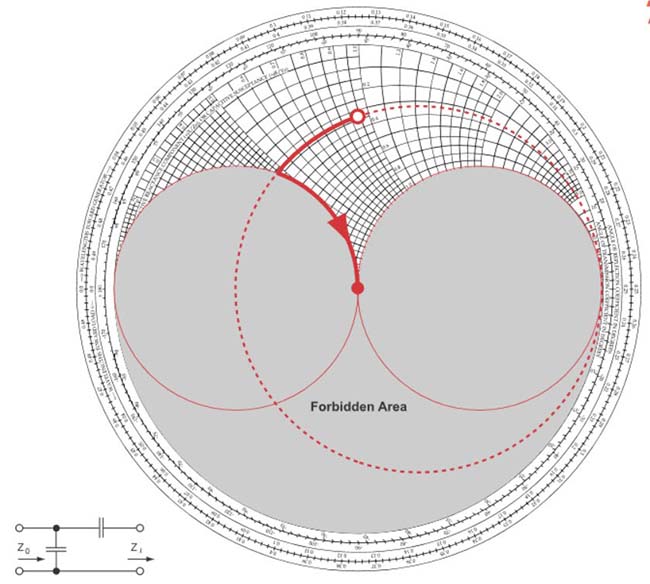
Fig. 35 : 7^ème type de réseau adaptateur : condensateur en série (parcours en sens antihorlogique sur un cercle à résistance constante) et condensateur parallèle (parcours en sens horlogique sur un cercle à conductance constante). Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

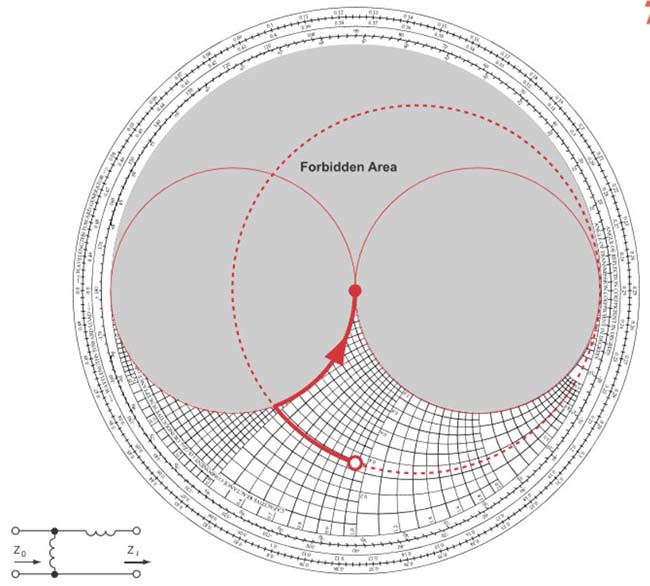
Fig. 36 : 8^ème type de réseau adaptateur : bobine d’induction en série (parcours en sens horlogique sur un cercle à résistance constante) et bobine d’induction parallèle (parcours en sens anti horlogique sur un cercle à conductance constante). Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.
On remarquera sur les huit figures ci-dessus que le premier déplacement se termine chaque fois sur un cercle à résistance constante unitaire ou sur un cercle à conductance constante unitaire. Dès qu’un cercle unitaire est rejoint, c’est le ticket assuré pour le voyage vers le centre de la terre : le deuxième déplacement s’effectue le long de ce cercle unitaire et rejoint le centre de l’abaque de Smith.

Les huit types de réseaux en L peuvent être répartis en six zones de l’abaque de Smith où l’impédance est adaptable par un circuit en « L » dont le type est répertorié et indiqué (voir figure suivante).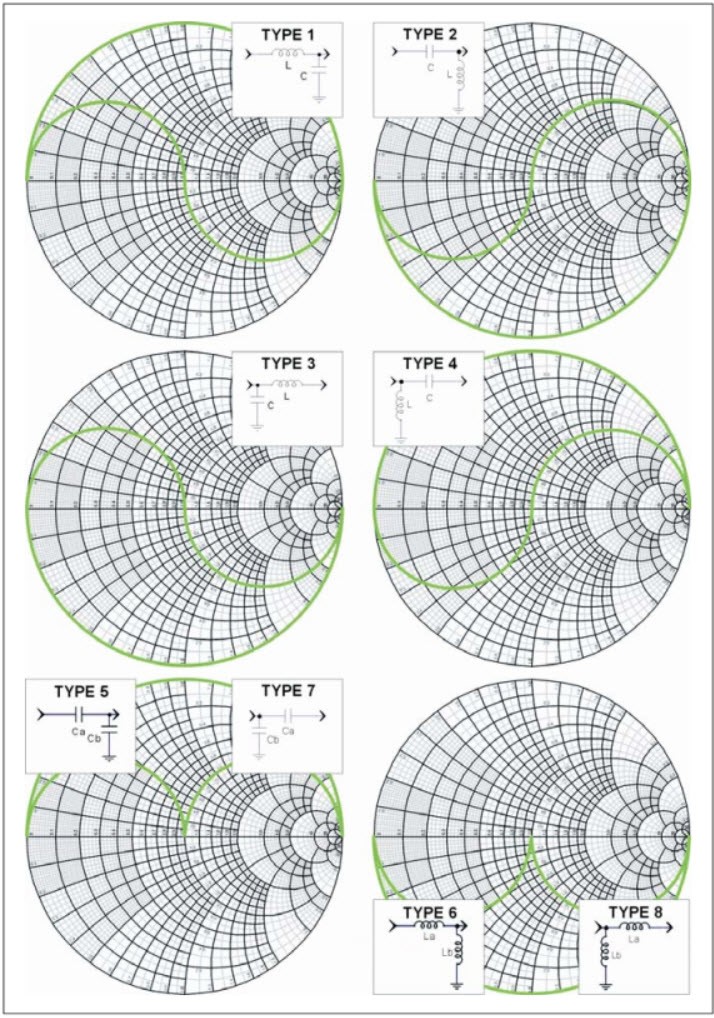

Fig. 37 : Représentation des six zones entourées d’une ligne verte là-où une impédance est adaptable par le circuit en « L » indiqué. Source Agilent Keysight EEsof EDA (Electronic Engineering Software Electronic Design Automation), Matching Network Yin-Yang Part 1, March 2006, USA.

Quel circuit en « L » faut-il utiliser lorsqu’il y a plusieurs solutions possibles ?

Si le réseau d’adaptation doit être intégré à un circuit électronique actif (amplificateur, préamplificateur), alors il peut y avoir des conditions de schéma où l’on profite de la présence d’une bobine pour alimenter l’élément actif en courant continu et de la présence d’un condensateur pour bloquer cette composante continue lorsque le signal doit être acheminé à un étage suivant devant être libre de potentiel par rapport à l’étage précédent.

S’il n’y a pas de contraintes schématiques, alors il y a lieu de réaliser une simulation de la bande passante du circuit. Bien qu’un réseau soit calculé à une fréquence bien précise, on peut observer le coefficient de transmission du circuit dans une portion de bande de fréquence aux abords immédiats de la fréquence de travail pour laquelle le circuit a été calculé. Certains réseaux en « L » ressemblent à des filtres passe-bas, d’autre à des filtres passe-haut, d’autres sont un peu plus à large bande ou à bande un peu plus étroite. Le choix doit donc être guidé par la portion de bande que l’on veut privilégier et il y a lieu d’évaluer s’il est plus intéressant d’obtenir un circuit plus sélectif pour éventuellement contribuer à l’atténuation de signaux parasites adjacents à la fréquence de travail ou s’il vaut mieux utiliser un circuit à plus à large bande en fonction de la plage potentielle où peut se situer la fréquence de travail.

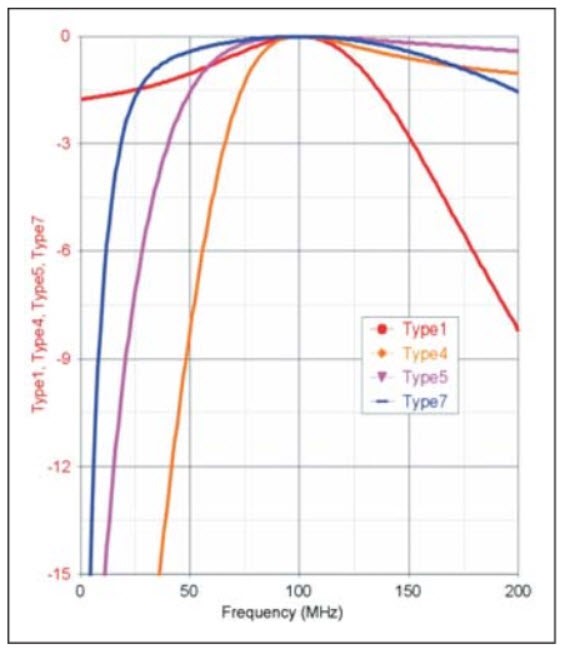
Fig. 38 : Réponse dans le domaine de la fréquence des types de réseaux en « L » des types 1, 4, 5 et 7 comme répertoriés à la figure précédente pour une adaptation à 100 MHz d’une impédance de charge de 25+j43,33 Ω à une impédance de source de 50 Ω. Source Agilent Keysight EEsof EDA (Electronic Engineering Software Electronic Design Automation), Matching Network Yin-Yang Part 1, March 2006, USA.

Une impédance de charge à adapter peut se situer sur l’abaque à un endroit où il peut y avoir jusqu’à quatre solutions différentes possibles comme illustré ci-dessous.

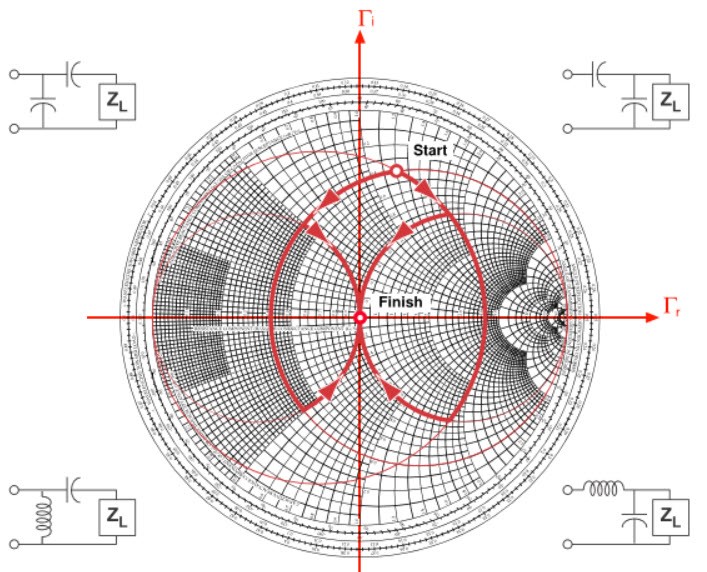
Fig. 39 : Quatre types de réseaux en « L » satisfont l’adaptation d’impédance pour la charge située en impédance normalisée sur l’abaque de Smith. Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

Par quoi commencer : un composant série ou parallèle en partant de la charge ?

Lorsque l’impédance de la charge est plus élevée que celle de la source (R_L>R_S), on commence par un composant parallèle du côté de la charge.
Lorsque l’impédance de charge est plus petite que celle de la source (R_L<R_S), on commence par un composant série du côté de la charge.

Exemple pratique de l’utilisation de l’abaque de Smith pour le calcul d’un réseau en « L » d’adaptation d’impédance :

Soit une charge d’impédance Z_C = 100+j100 Ω à une fréquence de 1 GHz que nous devons adapter à une impédance de source Z_S = 50+j0 Ω. Quelles sont les valeurs des composants du réseau adaptateur en « L » ?

L’impédance normalisée de la charge est z_C = 2+j2. Plaçons cette impédance sur l’abaque de Smith au point (1). En consultant la figure 37, on constate qu’il y a deux zones possibles où l’impédance est adaptable : soit par un circuit du type 1 avec un condensateur en parallèle et une bobine d’induction série, soit par un circuit du type 2 avec une bobine d’induction en parallèle et un condensateur série. Nous allons tracer les deux solutions sur deux abaques différentes.

Prenons le cas d’un réseau du type 1. Nous devons placer un condensateur en parallèle sur la charge. Pour réaliser cette opération, nous allons travailler avec les admittances, c’est-à-dire l’admittance de la charge et l’admittance du condensateur en parallèle sur celle-ci. Pour trouver l’admittance de la charge (voir figure 40), on trace un point diamétralement opposé au point (1) : on trace une droite passant par le point (1) et le centre de l’abaque, ensuite on reporte la distance entre le point (1) et le centre pour trouver le point (2) d’impédance lue 0,25-j0,25. Cette impédance lue au point (2) représente la valeur de l’admittance de la charge. Voir la figure 13 pour se remémorer le passage d’une impédance à une admittance. Traçons un cercle à conductance constante unitaire sur l’abaque. Nous allons effectuer un déplacement le long d’un cercle à résistance constante dans le sens horlogique jusqu’à ce que l’on intercepte le cercle de conductance unitaire au point (3) d’impédance lue 0,25+j0,42. Ce point (3) représente en réalité l’admittance équivalente du condensateur mis en parallèle sur la charge. Pour retrouver l’impédance équivalente de cette association parallèle, on trace un point diamétralement opposé au point (3) pour trouver le point (4) d’impédance de 1‑j1,8 qui se situe sur le cercle à résistance constante unitaire. Il nous reste à effectuer le deuxième déplacement à partir du point (4) sur le cercle à résistance constante unitaire dans le sens horlogique vers le centre de l’abaque au point (5).

Calcul des composants :

1^er déplacement : de 0,25-j0,25 vers 0,25+j0,42 soit une différence de susceptance capacitive de j0,42-(-j0,25) = +j0,67.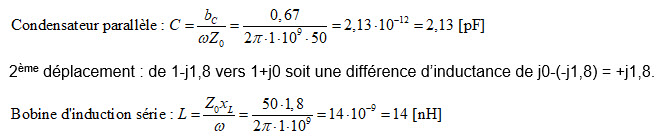

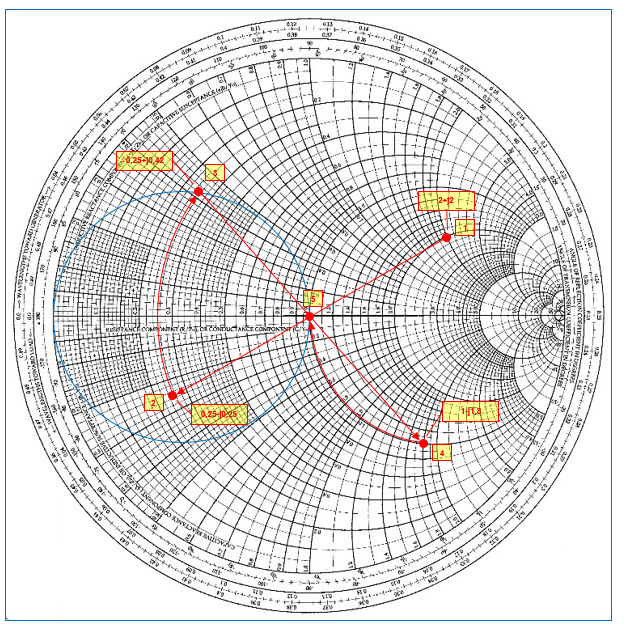
Fig. 40 : Adaptation d’une charge de 100+j100 Ω à 1 GHz à une source de 50+j0 Ω par un réseau adaptateur en « L » constitué d’un condensateur en parallèle de 2,13 pF sur la charge et d’une bobine d’induction de 14 nH en série avec la source. Graphisme : ON4IJ.
Prenons à présent le cas d’un réseau du type 2. Nous devons placer une bobine d’induction en parallèle sur la charge (voir figure 41). On réalise la même opération que ci-dessus pour trouver l’admittance de la charge au point (2) d’impédance lue 0,25‑j0,25. Traçons un cercle à conductance constante unitaire sur l’abaque. Nous allons effectuer un déplacement le long d’un cercle à résistance constante dans le sens antihorlogique jusqu’à ce que l’on intercepte le cercle de conductance unitaire au point (3’) d’impédance lue 0,25-j0,43. Ce point (3’) représente l’admittance équivalente de la bobine d’induction mise en parallèle sur la charge. Pour retrouver l’impédance équivalente de cette association parallèle, on trace un point diamétralement opposé au point (3’) pour trouver le point (4’) d’impédance de 1+j1,6 qui se situe sur le cercle à résistance constante unitaire. Il nous reste à effectuer le deuxième déplacement à partir du point (4’) sur le cercle à résistance constante unitaire dans le sens antihorlogique vers le centre de l’abaque au point (5).

Calcul des composants :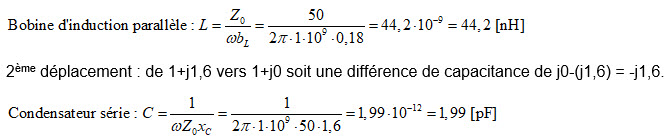

Voyons tout cela sur la figure suivante.

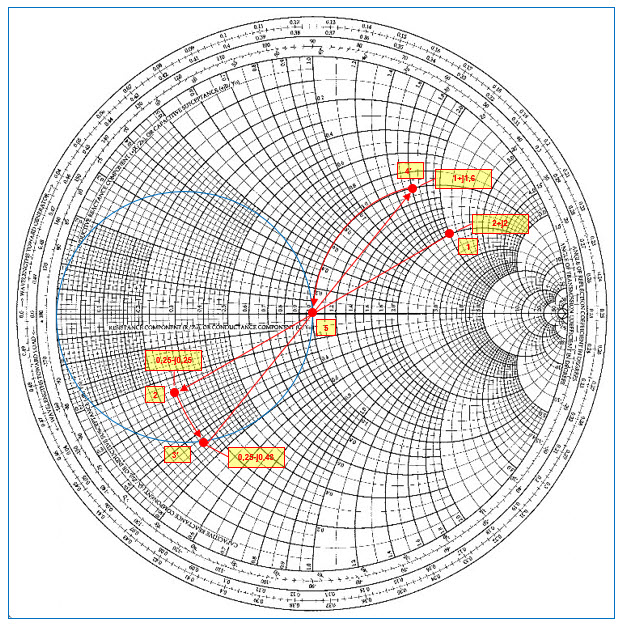
Fig. 41 : Adaptation d’une charge de 100+j100 Ω à 1 GHz à une source de 50+j0 Ω par un réseau adaptateur en « L » constitué d’une bobine d’induction en parallèle de 44,2 nH sur la charge et d’un condensateur de 1,99 pF en série avec la source. Graphisme : ON4IJ.
Jusqu’à présent, nous avons utilisé des réseaux adaptateurs en « L » sachant que ceux-ci sont calculés pour une fréquence bien précise. Cela peut représenter une contrainte lorsqu’on doit adapter une antenne sur toute une bande de fréquence, par exemple sur la bande des 2 m entre 144 MHz et 146 MHz. Toutefois, il est parfois intéressant de choisir un réseau d’adaptation à haute sélectivité.
La première amélioration que l’on peut apporter à un réseau adaptateur est d’utiliser un réseau en « PI » ou en « TÉ ». Un des premiers avantages est qu’un tel type de réseau permet d’adapter une résistance de charge d’une impédance aussi bien plus grande que plus petite que celle de la source. Un deuxième avantage est qu’on peut choisir le facteur de qualité du circuit et donc obtenir une meilleure maîtrise de la bande passante du réseau adaptateur. Une deuxième amélioration que l’on peut apporter est d’utiliser un réseau en échelle pour une adaptation à large bande.

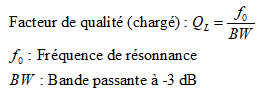
Le Q chargé tient compte des impédances qui chargent le réseau adaptateur à son entrée et à sa sortie : impédance de source (émetteur) et de charge (antenne).
Pour l’adaptation d’un oscillateur à une charge, on privilégie un facteur de qualité élevé pour éliminer les signaux parasites et harmoniques à la sortie du circuit.
Pour l’adaptation d’un système large bande à une charge, on privilégie un facteur de qualité relativement faible pour obtenir une adaptation satisfaisante sur toute la bande utile.
Le facteur de qualité à un nœud de connexion du réseau adaptateur peut aussi être défini comme le rapport entre la réactance et la résistance présentes à ce nœud. Cela va nous aider à tracer un quatrième réseau de cercles sur l’abaque de Smith (1 : résistance constante ; 2 : réactance constante ; 3 : SWR constant) ; quatrième réseau : les cercles à Q_n constant.

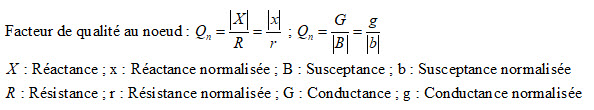
Les cercles à Q_n constant sont tracés sur l’abaque de Smith sous forme d’arcs qui commencent tous à r = x = 0 et se terminent tous à r = x = ∞. Les coordonnées du centre de ces cercles se situent en abscisse x = 0 et en ordonnée cartésienne y = +/‑(1/Q_n) ; y = +/-1 est situé sur le périmètre en haut et en bas de l’abaque ; les graduations sont linéaires sur l’axe y.

Dans les conditions d’adaptation parfaite, la relation entre le Q_L chargé et le Q_n au nœud est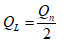
:

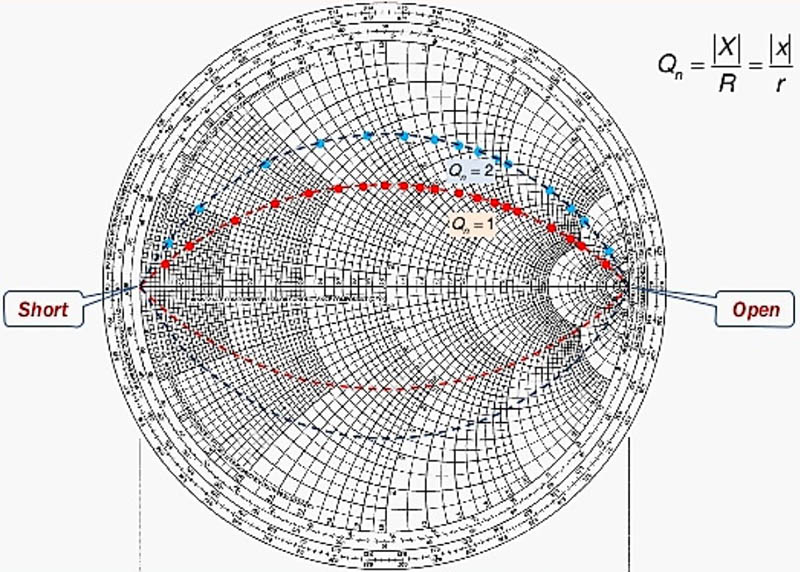
Fig. 42 : Cercles à Q_n constant tracés sur l’abaque de Smith. Source : Resonnators and Impedance Matching with Lumped Elements, Chien-Jung Li, Department of Electronics Engineering, National Taipei University of Technology.
Les cercles à Q_n constant délimitent des zones en forme d’œil à l’intérieur desquelles devront se situer les amplitudes de déplacement sur les cercles à résistance ou conductance constante lors du calcul des réseaux adaptateurs pour un Q_n déterminé. Pour des réseaux adaptateurs à plusieurs réactances en cascade, le Q_n à chaque nœud reste constant.

La figure suivante montre les déplacements sur l’abaque pour le calcul de deux réseaux différents. Le premier : courbe verte en trait discontinu, est un réseau en « L » dont le résultat sur l’abaque donne l’information d’un Q_n = 4. Le deuxième : courbe brune en trait continu, est un réseau « en échelle » (Ladder Network) composé de quatre circuits en « L » en cascade et dont le Q_n est déterminé pour donner une valeur de Q_n = 1. Les déplacements suivent les cercles à résistance constante pour les composants séries du réseau et les cercles à conductance constante pour les composants parallèles.

Un circuit « PI » ou TÉ » est généralement choisi pour un réseau sélectif à Q_n élevé. Un circuit en échelle est généralement conçu pour être à large bande avec un Q_n faible.

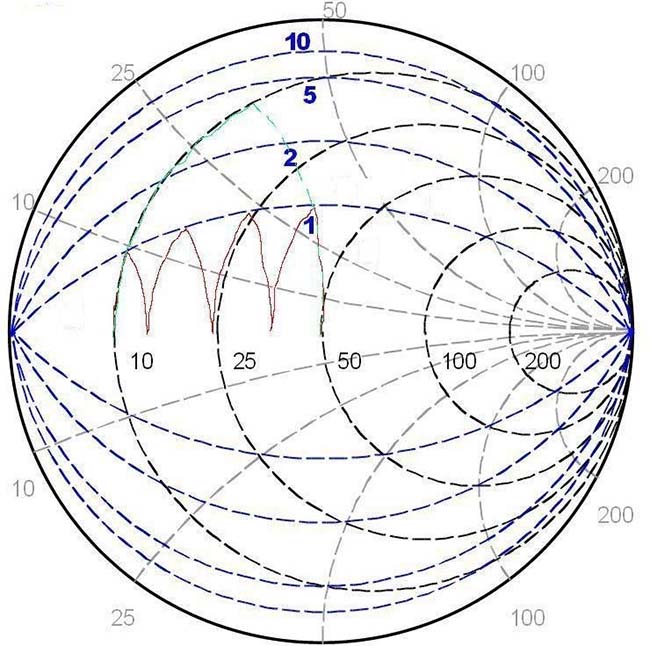
Fig. 43 : Cercles à Q_n constant avec tracés d’un premier réseau en « L » tracé en trait vert discontinu et d’un deuxième réseau en échelle (Ladder) large bande à quatre cellules en « L » en cascade tracé en trait brun continu. L’abaque est tracé directement pour Z₀ = 50 Ω. Source : Circuit Mason, Tutorial Gregory Kiesel, 2010.

Les déplacements pour un réseau adaptateur à large bande sont concentrés vers l’axe des résistances pures de l'abaque, c’est-à-dire que cela nécessite plus de composants aux réactances de valeurs faibles. On remarquera que l’impédance à adapter dans cet exemple est peu affectée de composante réactive pour ce réseau large bande.

Réseaux en « PI » et en « TÉ » pour une adaptation à haute sélectivité :

Nous reprendrons ci-dessous la méthode du calcul analytique décrite dans l’exposé intitulé : Resonnators and Impedance Matching with Lumped Elements de l’ingénieur Chien-Jung Li de l’Université Nationale en Technologie de Taipei. Ces réseaux seront ensuite illustrés sur l’abaque de Smith avec des cas concrets.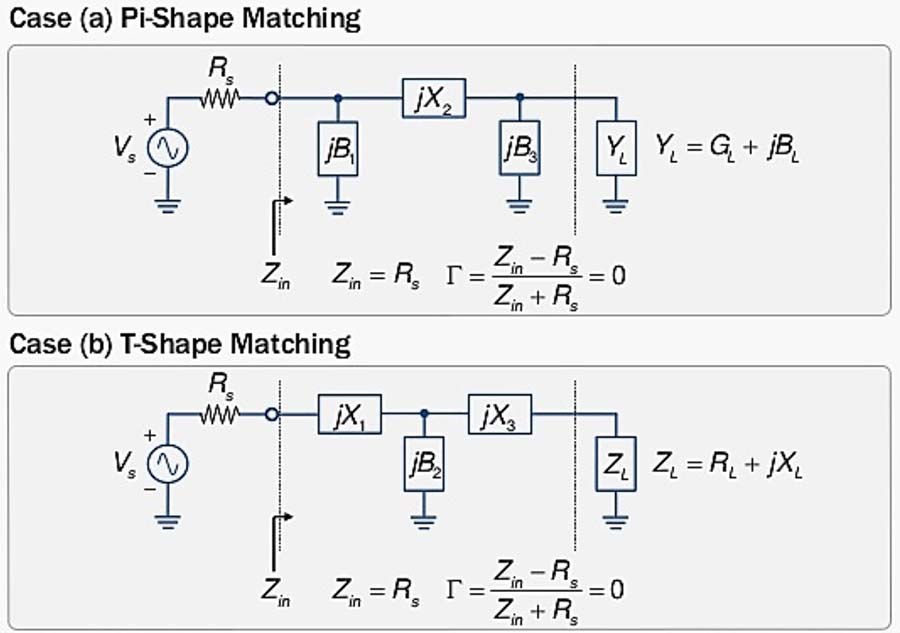

Fig. 44 : Réseaux en « PI » et en « TÉ ». Les composants séries sont sous la forme de réactance et les composants parallèles sont sous la forme de susceptance. La charge est parfaitement adaptée à la source et le coefficient de réflexion est nul à l’entrée du réseau. Source Chien-Jung Li, Université de Taipei.

Pour calculer les réseaux en « PI » et en « TÉ », ceux-ci peuvent être décomposés en deux parties en fractionnant l’élément central. Le résultat est comparable à deux réseaux en « L » en cascade. Dans un circuit « PI » l’élément central est décomposé en deux éléments en série. Dans un circuit « TÉ », l’élément central est décomposé en deux éléments en parallèle. Comme il faut bien attribuer une impédance entre les deux circuits « L » en cascade, on choisit une impédance intermédiaire que l’on peut représenter par une résistance virtuelle R_v. En aucun cas il s’agit de rajouter une résistance au schéma ! La résistance virtuelle représente tout simplement une impédance intermédiaire pour pouvoir calculer chaque circuit en « L » : R_v sera l’impédance de sortie du premier réseau en « L » et R_v sera l’impédance d’entrée du deuxième réseau en « L ».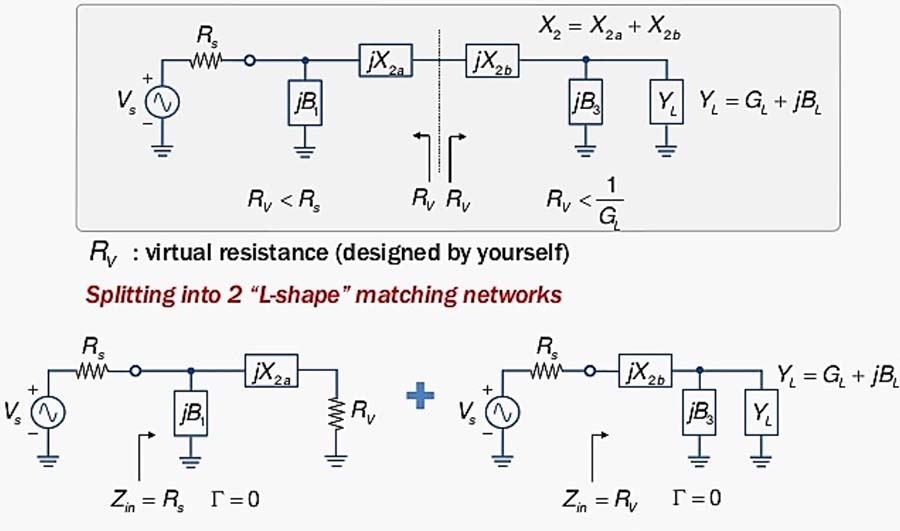

Fig. 45 : Réseau en « PI » décomposé en deux réseaux « L » en cascade. La résistance virtuelle R_V représente une impédance intermédiaire de calcul pour la sortie du premier réseau et pour l’entrée du deuxième réseau. Source Chien-Jung Li, Université de Taipei.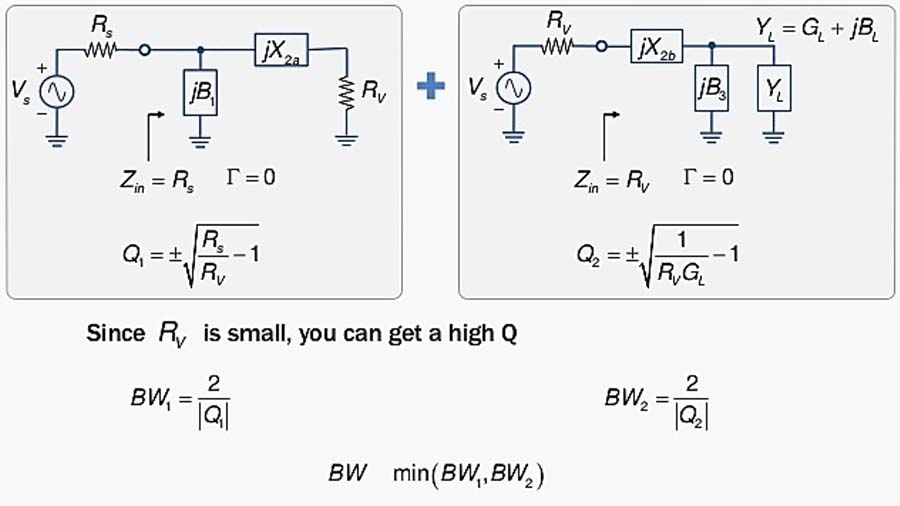

Fig. 46 : Réseau en « PI » décomposé. Le choix de la résistance virtuelle va déterminer le facteur de qualité du circuit et donc sa sélectivité. Source Chien-Jung Li, Université de Taipei.

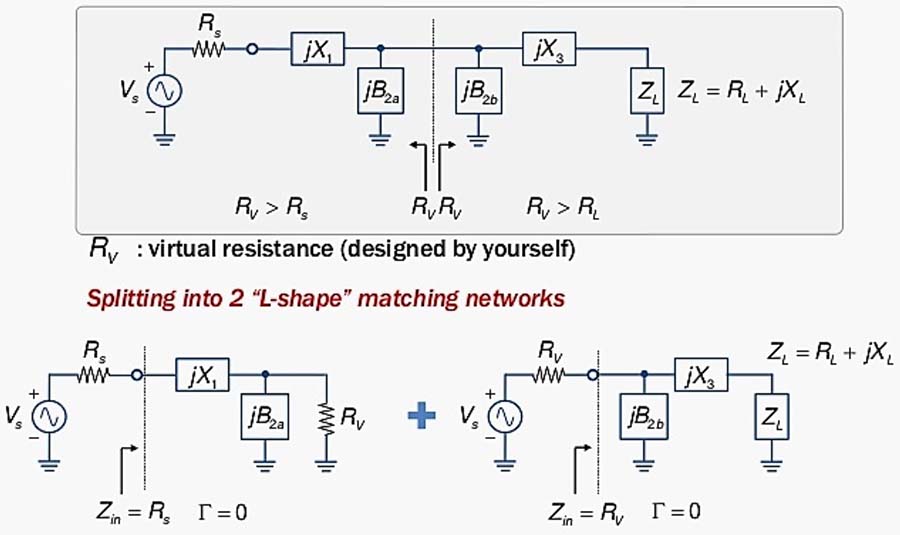
Fig. 47 : Réseau en « TÉ » décomposé en deux réseaux « L » en cascade. La résistance virtuelle R_V représente une impédance intermédiaire de calcul pour la sortie du premier réseau et pour l’entrée du deuxième réseau. Source Chien-Jung Li, Université de Taipei.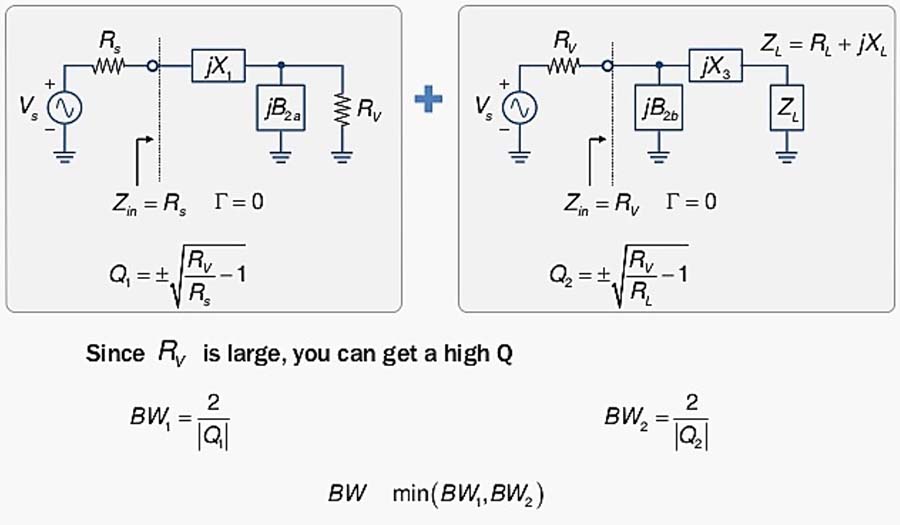

Fig. 48 : Circuit en « TÉ » décomposé. Le choix de la résistance virtuelle va déterminer le facteur de qualité du circuit et donc sa sélectivité. Source Chien-Jung Li, Université de Taipei.

Cas pratique : on veut adapter à une ligne de transmission de 50 Ω une antenne en dipôle replié dont l’impédance à la fréquence de résonnance à 100 MHz est de 300 Ω. On demande de calculer un réseau « PI » dont la bande passante est plus petite ou égale à 5 % de la fréquence de résonnance.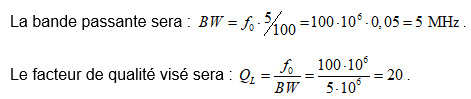

En décomposant le réseau « PI » en deux réseaux « L » nous allons calculer le facteur de qualité de ceux-ci et choisir le Q maximum entre Q₁ et Q₂.

Le réseau en « PI » admet quatre solutions :

Filtre passe-bas avec élément central à deux bobines d’induction en série ;
Filtre passe-haut avec élément central à deux condensateurs en série ;
Filtre passe-bande avec passe-bas en entrée et passe-haut en sortie ;
Filtre passe-bande avec passe-haut en entrée et passe-bas en sortie.

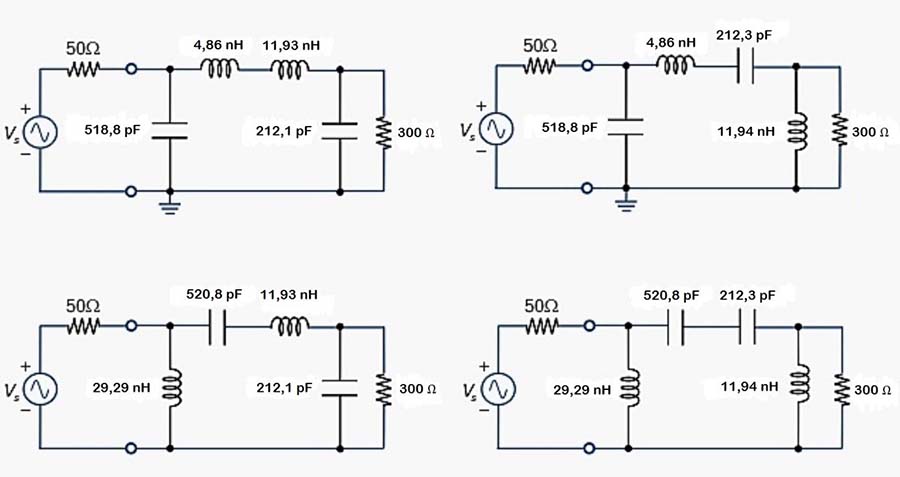
Fig. 49 : Réseau en « PI » décomposé calculé pour f₀ = 100 MHz avec les quatre possibilités de configuration. Source Chien-Jung Li, Université de Taipei.

Lorsque l’élément central est composé de deux bobines d’induction en série, elles peuvent se recombiner en une seule dont la valeur totale du coefficient d’induction est la somme des coefficients d’induction des deux bobines d’induction.
Lorsque l’élément central est composé de deux condensateurs en série, ils peuvent se recombiner en un seul dont l’inverse de la valeur totale de la capacité est la somme des inverses des capacités des deux condensateurs.
En général, les radioamateurs choisissent la solution du filtre passe-bas avec élément central à bobine d’induction pour le réseau en « PI » qui est connu sous l’appellation de circuit Jones ou circuit Collins du nom de leurs inventeurs. Il est très utilisé comme circuit d’accord de sortie de l’étage amplificateur final de puissance à tubes radio fonctionnant en classe C dans les stations radioamateurs : le condensateur d’entrée et celui de sortie sont des condensateurs variables (Tuning, Loading) et la bobine centrale est constituée de plusieurs bobines en série qui sont commutées selon les différentes gammes d’ondes décamétriques en ondes courtes.

Tracé du réseau en « PI » sur l’abaque de Smith :

Nous prendrons la configuration du filtre passe-bas. Pour une fréquence de 100 MHz, les valeurs des composants sont :

Z_L = 300 Ω ; C_B3 = 212,1 pF ; L_X2b = 11,93 nH ; L_X2a = 4,86 nH ; C_B1 = 518,8 pF. Comme les deux bobines d’induction en série se recombinent, on aura :

L_X2 = 11,93+4,86 = 16,79 nH.

L’impédance normalisé de la charge est z_L = 300/50 = 6+j0. Plaçons cette impédance normalisée sur l’abaque au point (1). Comme nous allons mettre un condensateur de 212,1 pF en parallèle sur la charge, on va convertir l’impédance de la charge en admittance normalisée au point (2) diamétralement opposé et y ajouter la susceptance capacitive normalisée du condensateur C_B3. Au point (2), nous avons l’admittance de la charge :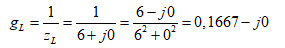

Ajouter un condensateur en parallèle sur la charge revient à effectuer un déplacement d’une amplitude de susceptance capacitive de :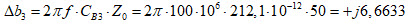

Du point (2) on se déplace le long d’un cercle à résistance constante vers le point (3) d’impédance lue correspondant à une admittance y₁ de :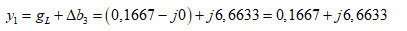

Comme nous allons rajouter une bobine d’induction en série, on va devoir convertir l’admittance y₁ en impédance z₁ en prenant le point (4) diamétralement opposé au point (3) :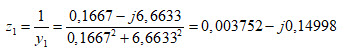

Ajouter une bobine d’induction en série revient à effectuer un déplacement d’une amplitude d’inductance de :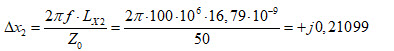

Du point (4) on se déplace le long d’un cercle à résistance constante vers le point (5) d’une impédance z₂ de :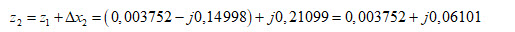

Comme nous allons rajouter un condensateur de 518,8 pF en parallèle sur z₂, on va convertir l’impédance z₂ en admittance y₂ en prenant le point (6) diamétralement opposé au point (5).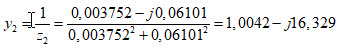

On remarque que nous sommes sur le cercle à résistance constante unitaire car 1,0042-j16,329 ≈ 1-j16,329.
Ajouter un condensateur en parallèle sur y₂ revient à effectuer un déplacement d’une amplitude de susceptance capacitive de :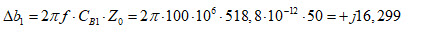

Du point (6) on se déplace le long d’un cercle à résistance constante vers le point (7) d’impédance lue correspondant à une admittance y₃ de :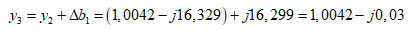

On remarque que nous arrivons pratiquement au centre de l’abaque. L’impédance d’entrée du réseau est z₃ :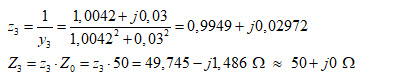

L’impédance d’entrée du réseau en « PI » que nous venons de calculer est parfaitement adaptée à la source d’impédance 50 Ω.
Visualisons tout cela sur l’abaque de Smith à la page suivante.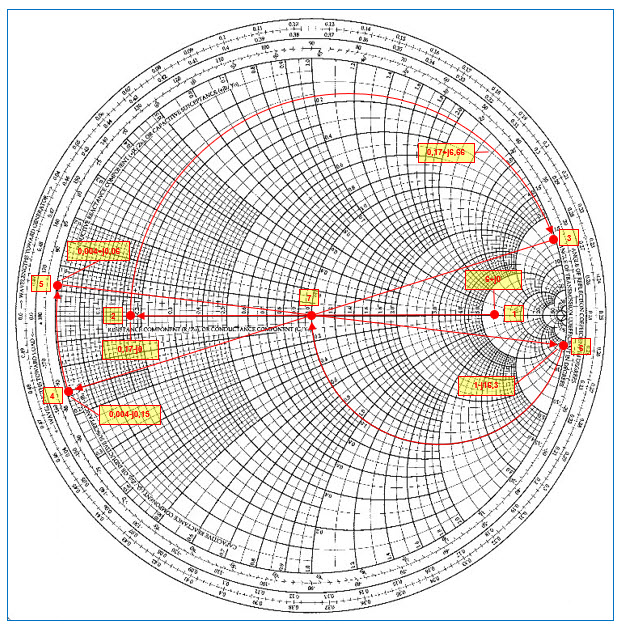

Fig. 50 : Tracé sur l’abaque de Smith d’un réseau en « PI » calculé pour une charge de 300 Ω et pour une source de 50 Ω sur une fréquence de travail de 100 MHz avec une bande passante de 5 %, c’est-à-dire de 5 MHz. Graphisme : ON4IJ.

Ci-dessous on peut observer une simulation du réseau en « PI » calculé ci-dessus avec la réponse dans le domaine de la fréquence sur deux graphiques : le premier donnant l’amplitude et la phase, le second la partie réelle et imaginaire de l’impédance d’entrée.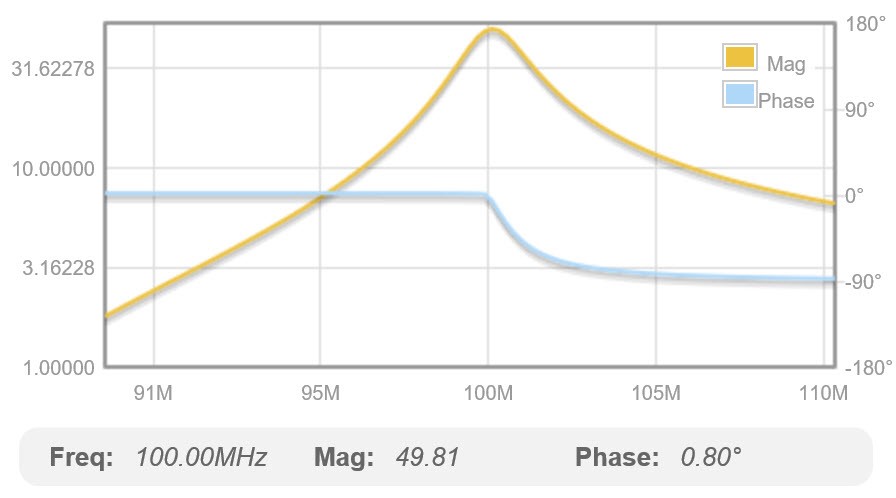

Fig. 51 : Diagramme d’amplitude et de phase de la transmission (S₂₁) du réseau en « PI » calculé pour f₀ = 100 MHz avec un Q_n de 40. Source Internet : EEWeb Electrical Engineering Community, ToolBox, PI-Match.

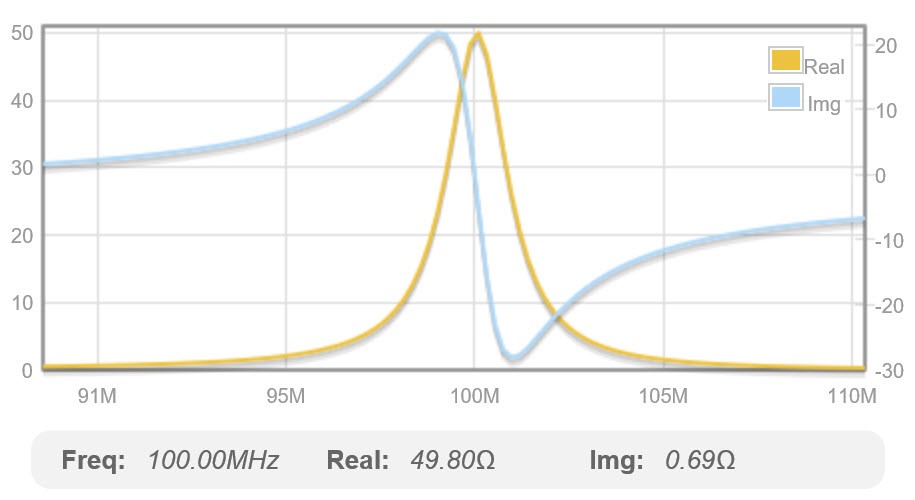
Fig. 52 : Diagramme (S₁₁) sous forme d’impédance complexe à l’entrée du réseau en « PI » avec partie réelle et partie imaginaire (f₀ = 100 MHz ; Q_n de 40). Source Internet : EEWeb Electrical Engineering Community, ToolBox, PI-Match.

Cas pratique : on veut adapter à une ligne de transmission de 50 Ω une antenne en dipôle replié dont l’impédance à la fréquence de résonnance à 100 MHz est de 300 Ω. On demande de calculer un réseau « TÉ » dont la bande passante est plus petite ou égale à 5 % de la fréquence de résonnance.

En décomposant le réseau « TÉ » en deux réseaux « L » nous allons calculer le facteur de qualité de ceux-ci et choisir le Q maximum entre Q₁ et Q₂.

Le réseau en « TÉ » admet quatre solutions :

Filtre passe-bas avec élément central à deux condensateurs en parallèle ;
Filtre passe-haut avec élément central à deux bobines d’induction en parallèle ;
Filtre passe-bande avec passe-bas en entrée et passe-haut en sortie ;
Filtre passe-bande avec passe-haut en entrée et passe-bas en sortie.

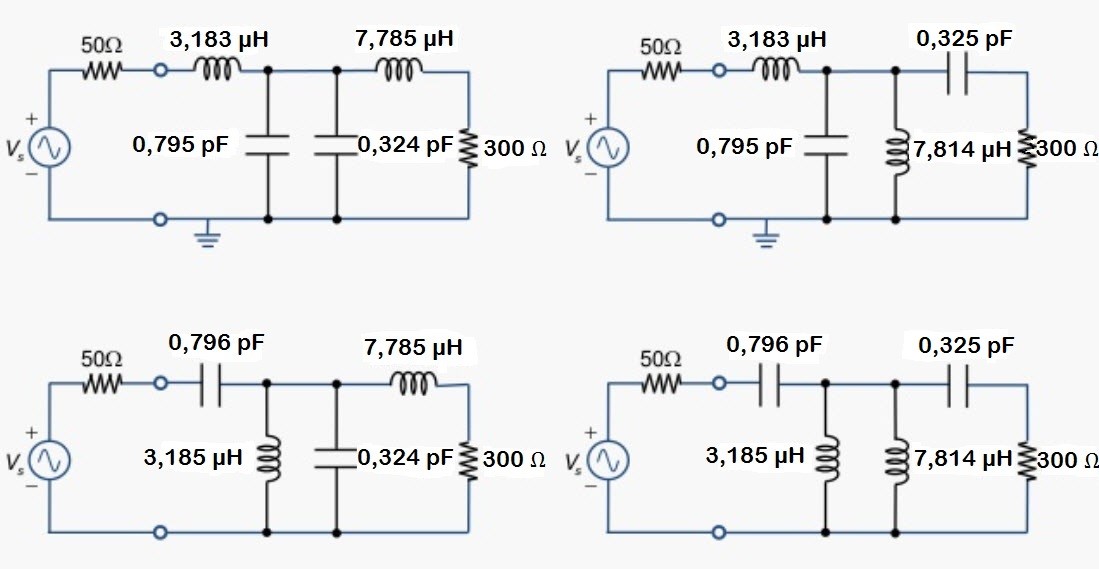
Fig. 53 : Réseau en « TÉ » décomposé calculé pour f₀ = 100 MHz avec les quatre possibilités de configuration. Source Chien-Jung Li, Université de Taipei.

Lorsque l’élément central est composé de deux condensateurs en parallèle, ils peuvent se recombiner en un seul dont la valeur totale est la somme des celles des deux condensateurs.
Lorsque l’élément central est composé de deux bobines d’induction en parallèle, elles peuvent se recombiner en une seule dont l’inverse de la valeur totale est la somme des inverses de celles des deux bobines d’induction.
En ce qui concerne les boîtes d’accord d’antenne (Antenna Tuner), les radioamateurs choisissent en général la solution du filtre passe-haut avec élément central à bobine d’induction. Celle-ci prend la forme d’une bobine montée sur un mandrin à rotor et à prise variable avec un curseur à roulette (« self à roulette »). Les deux condensateurs sont des modèles variables et parfois ceux-ci sont accouplés mécaniquement sur le même axe de façon à ce que le premier condensateur varie en capacité d’une manière inversement proportionnelle à la capacité du deuxième.

L’impédance d’entrée du réseau en « TÉ » que nous venons de calculer est parfaitement adaptée à la source d’impédance 50 Ω.
Visualisons tout cela sur l’abaque de Smith à la page suivante.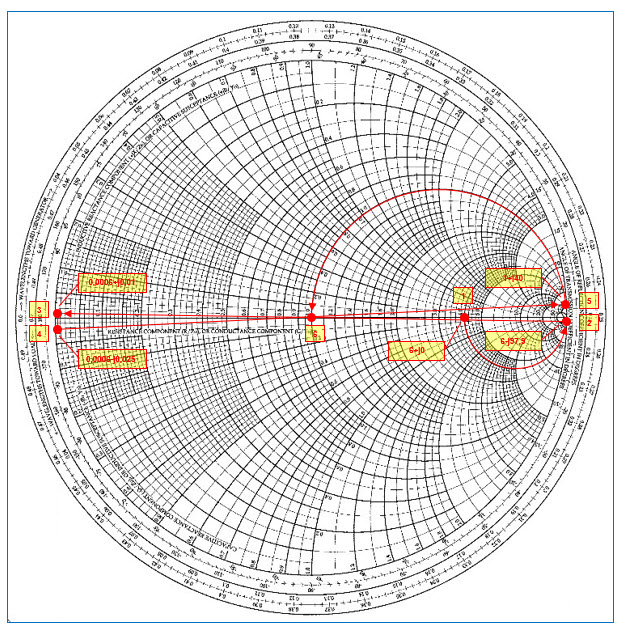

Fig. 54 : Tracé sur l’abaque de Smith d’un réseau en « TÉ » calculé pour une charge de 300 Ω et pour une source de 50 Ω sur une fréquence de travail de 100 MHz avec une bande passante de 5 %, c’est-à-dire de 5 MHz. Graphisme : ON4IJ.

On remarque que les tracés des déplacements sont de grandes amplitudes (composants fortement réactifs) et qu’ils se situent près du périmètre de l’abaque là-où se situent les cercles à Q constant de valeurs élevées.
Dans ce cas de figure, le Q est fort élevé pour un réseau en « TÉ » et les valeurs des condensateurs sont extrêmement faibles. Le calcul analytique ici est indispensable car les impédances et admittances placées sur l’abaque de Smith se situent dans des zones où la résolution des valeurs est insuffisante pour un calcul précis.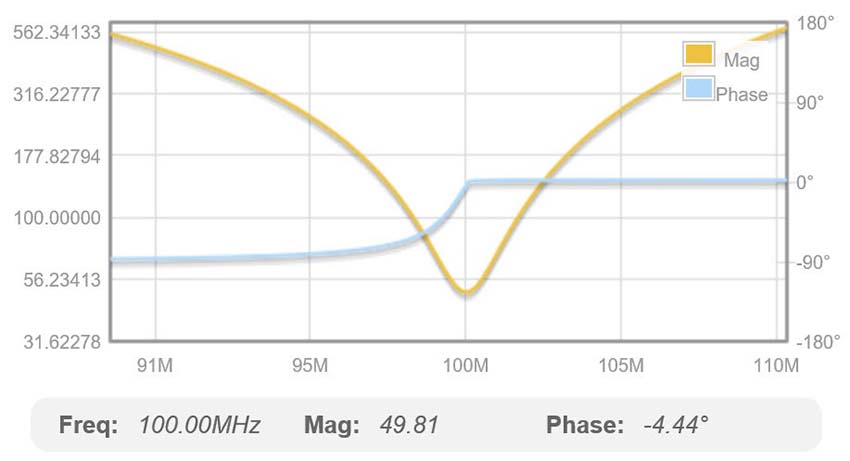

Fig. 55 : Diagramme d’amplitude et de phase de la transmission (S₂₁) du réseau en « TÉ » calculé pour f₀ = 100 MHz avec un Q_n de 40. Source Internet : EEWeb Electrical Engineering Community, ToolBox, T-Match.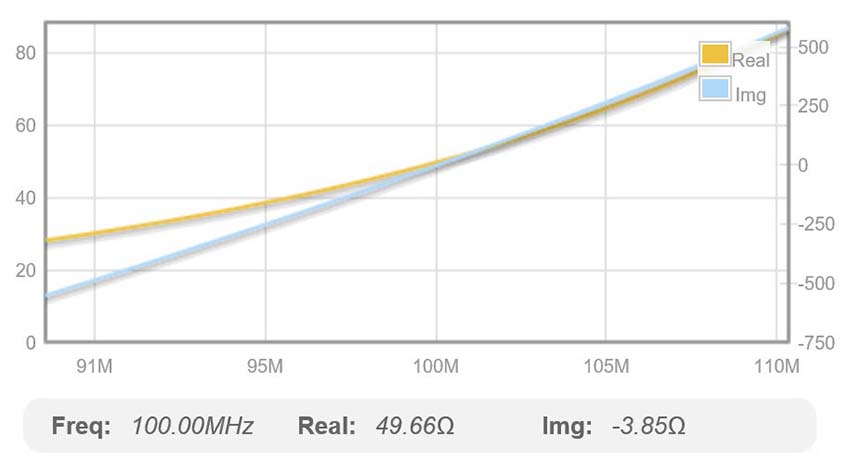

Fig. 56 : Diagramme (S₁₁) sous forme d’impédance complexe à l’entrée du réseau en « TÉ » avec partie réelle et partie imaginaire (f₀ = 100 MHz ; Q_n de 40). Source Internet : EEWeb Electrical Engineering Community, ToolBox, T-Match.

Réseaux en échelle en « double L » pour adaptation à large bande :

Les réseaux en échelle peuvent comporter plusieurs cellules et devenir tellement complexes que leur calcul s’effectue en général sur des logiciels spécifiques. Toutefois on peut constituer un réseau en échelle sur base de deux circuits « L » en cascade pour une adaptation large bande et visualiser le tracé du calcul sur l’abaque de Smith.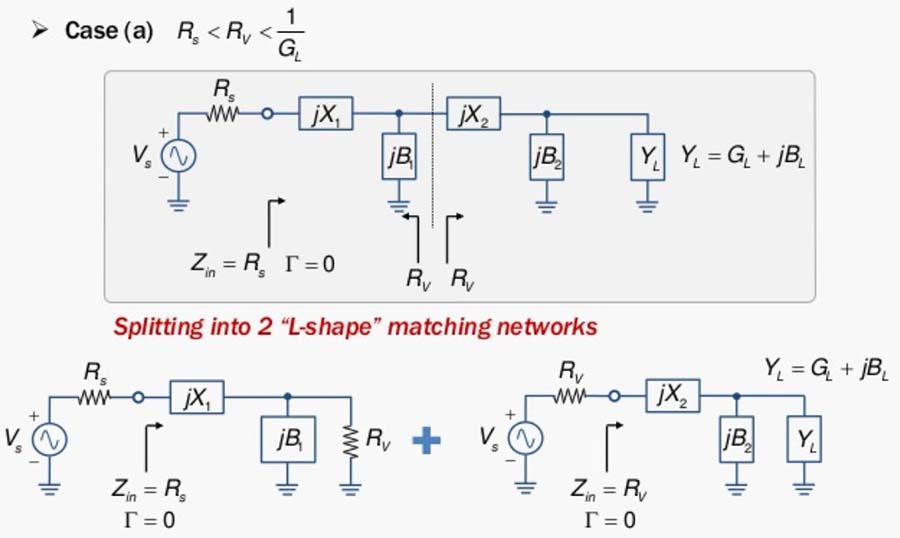

Fig. 57 : Réseau en échelle constitué de deux réseaux en « L » pour des charges d’impédance de valeur plus élevée que celle de la source. Source Chien-Jung Li, Université de Taipei.

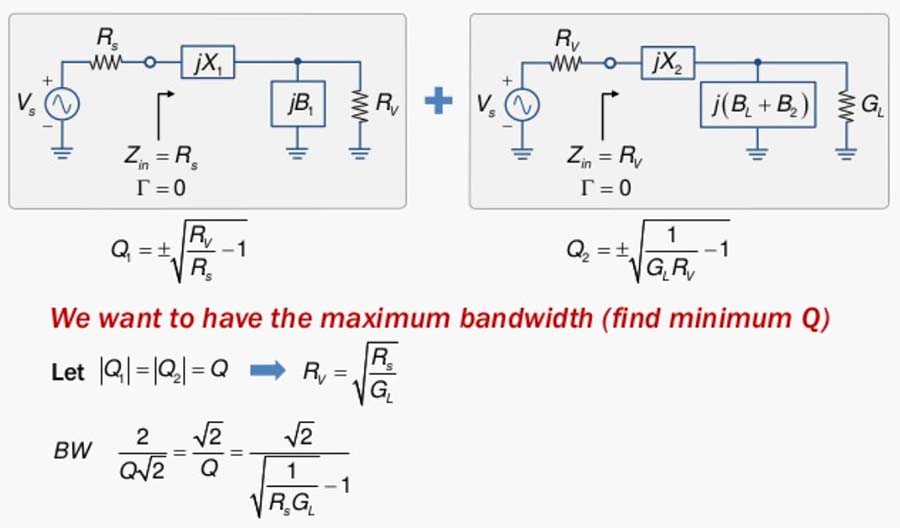
Fig. 58 : Décomposition en deux réseaux en « L » et choix d’un Q faible pour une adaptation large bande. Source Chien-Jung Li, Université de Taipei.

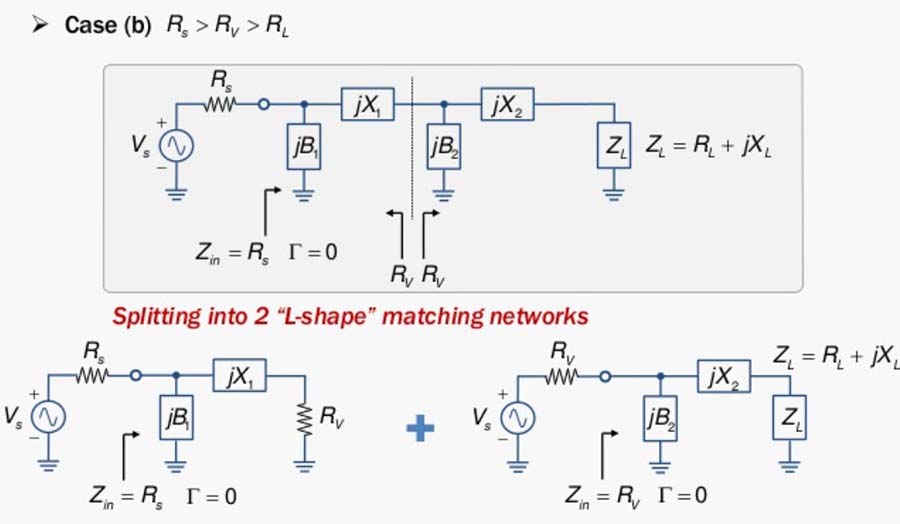
Fig. 59 : Réseau en échelle constitué de deux réseaux en « L » pour des charges d’impédance de valeur plus faible que celle de la source. Source Chien-Jung Li, Université de Taipei.

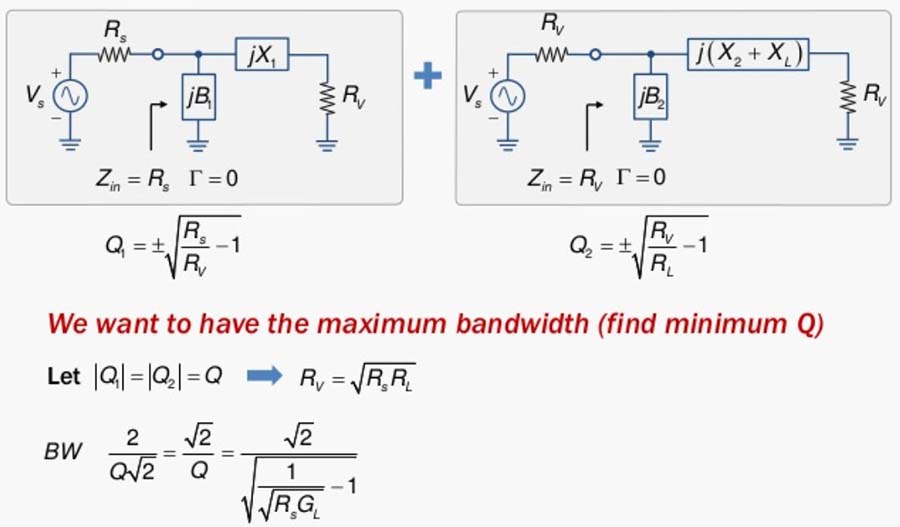
Fig. 60 : Décomposition en deux réseaux en « L » et choix d’un Q faible pour une adaptation large bande. Source Chien-Jung Li, Université de Taipei.

Cas pratique : on veut adapter à une ligne de transmission de 50 Ω une antenne en dipôle replié dont l’impédance à la fréquence de résonnance à 100 MHz est de 300 Ω. On demande de calculer un réseau « en double L » dont la bande passante est la plus large possible.

En décomposant le circuit en deux réseaux « L » nous allons calculer le facteur de qualité le plus faible possible. Pour cela, nous allons choisir une valeur de résistance virtuelle égale à la moyenne géométrique entre la valeur de la source et celle de la charge avec R_S < R_V < R_L

Le réseau en « double L » admet quatre solutions :

Filtre passe-bas ;
Filtre passe-haut ;
Filtre passe-bande avec passe-bas en entrée et passe-haut en sortie ;
Filtre passe-bande avec passe-haut en entrée et passe-bas en sortie.

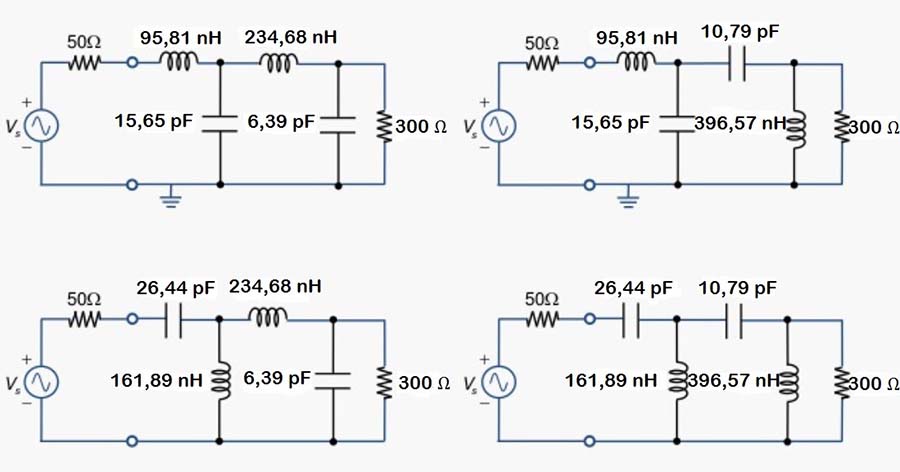
Fig. 61 : Réseau en « double L » calculé pour f₀ = 100 MHz, Q_n= 1,2 avec les quatre possibilités de configurations. Source Chien-Jung Li, Université de Taipei.

Tracé du réseau en « double L » sur l’abaque de Smith :

Nous prendrons la configuration du filtre passe-bas. Pour une fréquence de 100 MHz, les valeurs des composants sont :
Z_L = 300 Ω ; C_B2 = 6,39 pF ; L_X2 = 234,68 nH ; C_B1 = 15,65 pF ; L_X1 = 95,81 nH.

L’impédance normalisé de la charge est z_L = 300/50 = 6+j0. Plaçons cette impédance normalisée sur l’abaque au point (1). Comme nous allons mettre un condensateur de 6,39 pF en parallèle sur la charge, on va convertir l’impédance de la charge en admittance normalisée au point (2) diamétralement opposé et y ajouter la susceptance capacitive normalisée du condensateur C_B2. Au point (2), nous avons l’admittance de la charge :

L’impédance d’entrée du réseau en « double L » que nous venons de calculer est parfaitement adaptée à la source d’impédance 50 Ω.
Visualisons tout cela sur l’abaque de Smith à la page suivante.

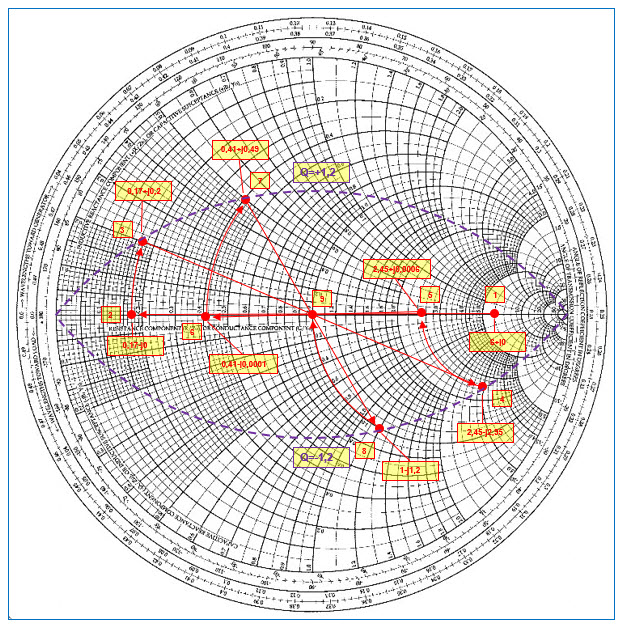
Fig. 62 : Tracé sur l’abaque de Smith d’un réseau en « double L » large bande calculé pour une charge de 300 Ω et pour une source de 50 Ω sur une fréquence de travail de 100 MHz avec un Q_n = 1,2. Graphisme : ON4IJ.

On remarque que les amplitudes de déplacement sur l’abaque de Smith se situent toutes à l’intérieur de l’œil formé par les deux cercles à Q constant : soit entre l’axe des résistances pures et le cercle Q = +1,2 soit entre cet axe et le cercle Q = -1,2. C’est bien cette valeur du facteur de qualité Q = ±1,2 que nous avions calculée au départ pour obtenir le maximum de bande passante.

Variation d’impédance en fonction de la fréquence :

Quel que soit le réseau d’adaptation d’impédance, il y a lieu de se rappeler que l’impédance complexe d’une charge varie en fonction de la fréquence et que les réactances qui composent un réseau d’adaptation varient aussi avec la fréquence.

Pour visualiser la variation d’impédance complexe en fonction de la fréquence on utilise un analyseur de réseau vectoriel en sélectionnant l’affichage de l’abaque de Smith. On peut alors mieux cibler les caractéristiques d’un réseau d’adaptation de manière à optimiser l’adaptation sur une bande passante déterminée.

Dans l’exemple suivant, nous allons illustrer un circuit qui adapte parfaitement la charge au milieu de la bande passante mais aux deux extrémités de la bande passantes, la partie réactive du circuit a pour conséquence d’augmenter le SWR : celui-ci se situe sur un cercle à SWR constant sur l’abaque. En fonction du lieu géométrique de la variation d’impédance et en fonction de la forme de ce lieu, on peut volontairement déplacer l’impédance présente au milieu de la bande de manière à mieux positionner les impédances aux extrémités de la bande de fréquence utile : on s’aperçoit que celles-ci sont contenues sur un cercle à SWR constant de valeur inférieure.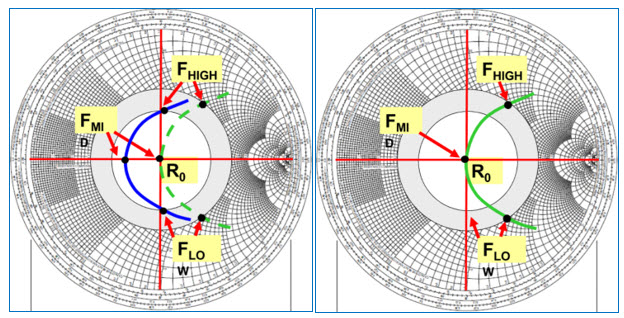

Fig. 63 et 64 : Déplacement de l’impédance en milieu de bande pour améliorer la bande passante d’un réseau. Source South Florida DX association, Kai Siwiak KE4PT (AMSAT), Ed Callaway N4II (ARRL), 9 Août 2010.

Afin de mieux maîtriser la forme et le lieu géométrique de l’impédance en fonction de la fréquence pour qu’il se situe dans un cercle à SWR constant déterminé, on peut utiliser un réseau en « L » précédé d’un réseau résonnant. On procède en deux temps.

En premier lieu, on détermine un réseau en « L » de manière à ce que l’impédance adaptée se situe sur l’axe des résistances pures de l’abaque de Smith (voir figure 65) mais avec un décalage vers la gauche (point A) ou vers la droite (point B) par rapport au centre de l’abaque. Les points A et B se situent sur un cercle à SWR constant dont la valeur représente le meilleur compromis. On utilisera un réseau qui introduit le minimum de réactance pour conserver une bande passante maximale.

En deuxième lieu, on « enroule » le lieu géométrique d’impédance en fonction de la fréquence à l’intérieur du cercle à SWR constant du meilleur compromis en ajoutant un circuit résonnant série ou parallèle requis selon le cas de figure pour obtenir un circuit en « PI résonnant » ou en « TÉ résonnant. La figure suivante illustre les différentes possibilités de réseaux sur l’abaque de Smith.

<imgsrc="/images/electronique/abaque-smith/abaque-smith-65.jpg" alt="abaque-smith-65">

Fig. 65 : Réseaux en « PI résonnant » et en « TÉ résonnant » pour la maîtrise du SWR sur une large bande selon la variation d’impédance en fonction de la fréquence. Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

Les deux figures suivantes illustrent l’avant et l’après « enroulement » du lieu géométrique d’impédance complexe en fonction de la fréquence à l’intérieur d’un cercle à SWR constant. L’exemple est repris du livre Antenna Impedance Matching de Wilfred N. Caron publié par l’ARRL.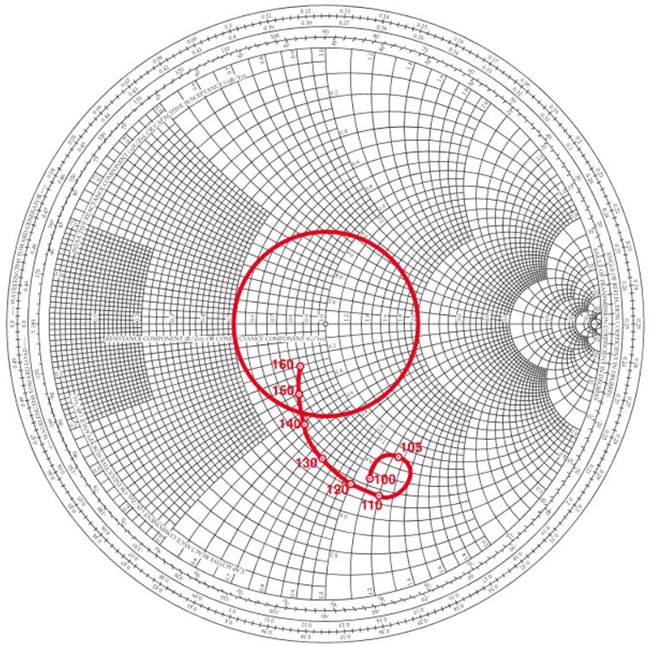

Fig. 66 : Lieu géométrique d’impédance complexe sur l’abaque de Smith d’une antenne VHF entre 100 MHz et 160 MHz. Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

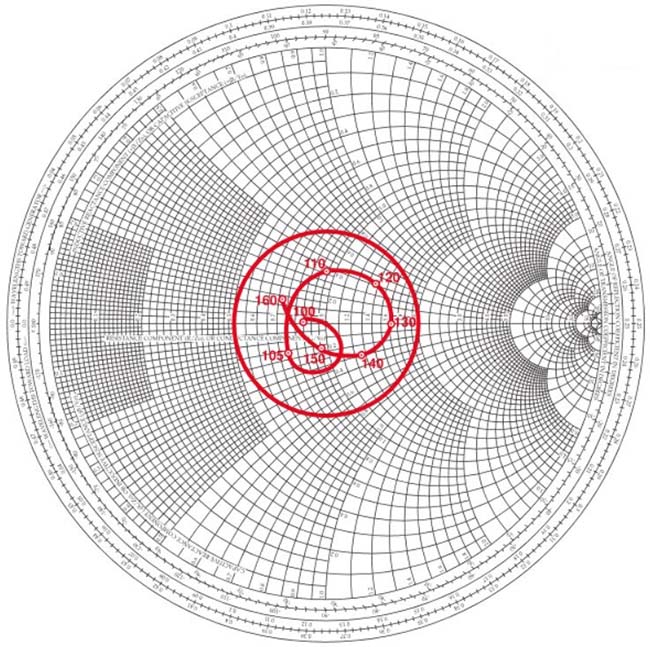
Fig. 67 : Lieu géométrique d’impédance complexe de la même antenne VHF mais avec un réseau adaptateur large bande optimisé pour contenir le SWR à l’intérieur d’un cercle à SWR constant d’une valeur de 1,67:1. Source Foothills Amateur Radio Society (FARS) K6YA, Steve Stearns K6OIK, ARRL Pacificon 2001.

Adaptation par Stub :

Qu’est-ce qu’un Stub ?

Il s’agit d’un segment de ligne de transmission dont une extrémité est soit en court-circuit soit en circuit ouvert et dont l’autre extrémité est placée soit en série soit en parallèle sur une ligne de transmission à une certaine distance de la charge.

Un segment de ligne de transmission se comporte, selon sa longueur et à une fréquence donnée, comme un condensateur ou comme une bobine d’induction. Autrement dit ce segment présente une réactance (ou une susceptance) pure, positive ou négative.

Rappelons-nous que lorsqu’on se déplace le long d’une ligne de transmission à partir de la charge en direction de la source, l’impédance varie mais sa valeur reste située sur un cercle à SWR constant de l’abaque de Smith. En se déplaçant sur ce cercle dans le sens horlogique (Toward Generator), on parvient à croiser le cercle à résistance constante unitaire (dans l’intention de placer Stub en série) ou bien le cercle à conductance constante unitaire (dans l’intention de placer un Stub parallèle). L’amplitude du déplacement sur le cercle à SWR constant va permettre de calculer la distance à laquelle le Stub doit être placé par rapport à la charge.

Au point de croisement entre le cercle à SWR constant et le cercle unitaire de l’abaque, on peut lire la valeur de la réactance (ou de la susceptance) présente à cet endroit de la ligne de transmission où va être placé le Stub. Il reste à calculer la longueur du Stub pour que la réactance (ou susceptance) de celui-ci soit égale mais de signe opposé à celle qui est présente à l’endroit de la ligne où le Stub doit être placé. La réactance (ou susceptance) du Stub annule celle qui est présente dans la ligne de transmission à l’endroit où est placé le Stub, ce qui revient à se déplacer sur le cercle unitaire en direction du centre de l’abaque pour une adaptation parfaite à l’impédance caractéristique de la ligne.

La réactance (ou la susceptance) d’un Stub à la fréquence de travail est fonction de sa longueur et du type de terminaison à son extrémité : soit un court-circuit, soit un circuit ouvert. Il y a lieu de se rappeler que la longueur de ce segment de ligne de transmission se calcule en longueur d’onde électrique de cette portion de ligne en tenant compte de son facteur de vélocité.

Les circuits adaptateurs d’impédance ou d’admittance à base de Stubs font partie des réseaux à éléments distribués car la réactance d’un Stub est distribuée sur sa longueur contrairement aux réseaux à éléments localisés constitués de condensateurs ou de bobines d’induction.

Calcul de la réactance (ou de la susceptance) d’un Stub en fonction de la fréquence et de sa longueur :

Remarquecar une longueur ne peut pas être négative ! La fonction tangente est définie à kπ près : tan(α) = tan(π+α) et tan(-α) = tan(π-α).

Ne pas oublier de paramétrer votre calculatrice scientifique en radians !

Réactance (ou susceptance) à l’entrée d’un Stub en court-circuit à la fréquence de travail et en fonction de sa longueur :

Fig. 68 : Stub en court-circuit. Graphisme : ON4IJ.

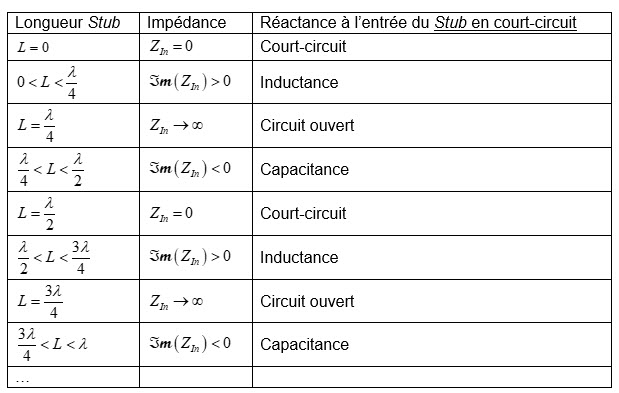
Réactance (ou susceptance) à l’entrée d’un Stub en circuit ouvert à la fréquence de travail et en fonction de sa longueur :

Fig. 69 : Stub en circuit ouvert. Graphisme : ON4IJ.

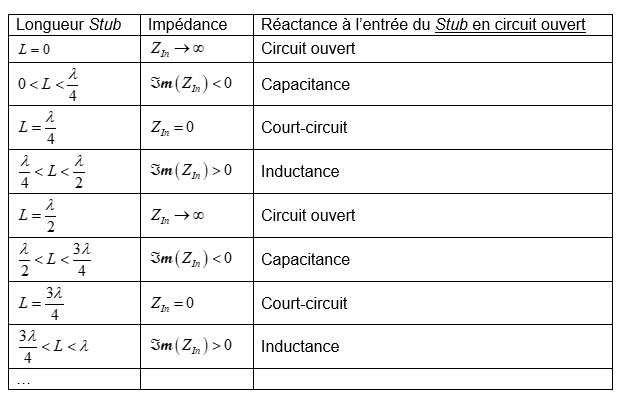
Les quatre figures suivantes illustrent les différentes configurations de placement d’un Stub pour adapter l’impédance d’une charge à celle d’une source de même impédance que celle de la ligne de transmission : Z_S = Z₀.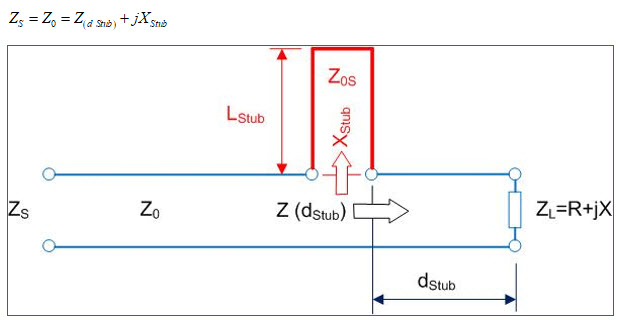

Fig. 70 : Stub en court-circuit placé en série sur la ligne de transmission. Graphisme : ON4IJ.

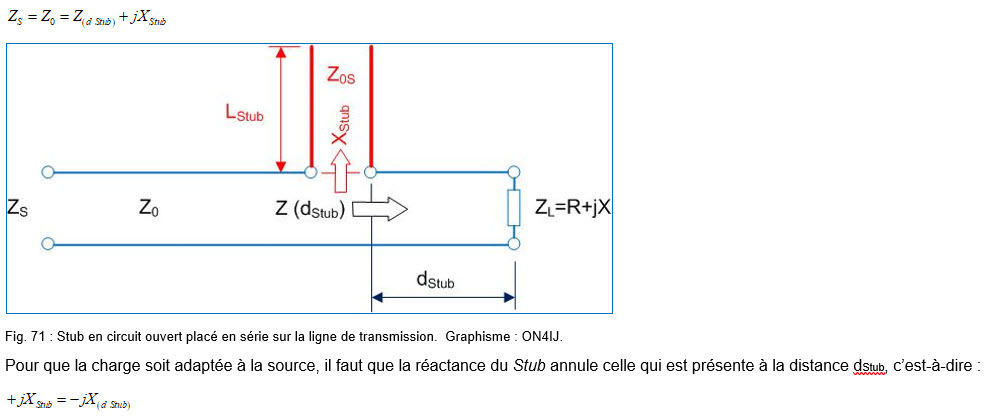
Fig. 71 : Stub en circuit ouvert placé en série sur la ligne de transmission. Graphisme : ON4IJ.

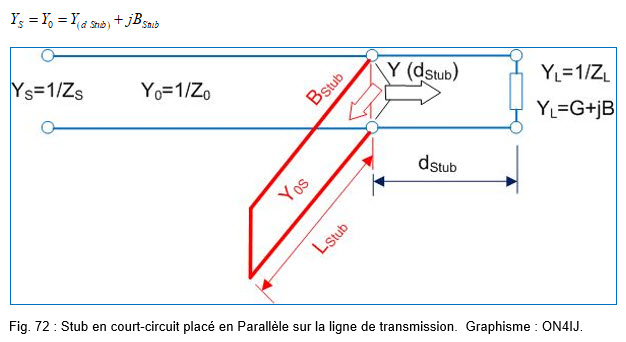
Fig. 72 : Stub en court-circuit placé en Parallèle sur la ligne de transmission. Graphisme : ON4IJ.

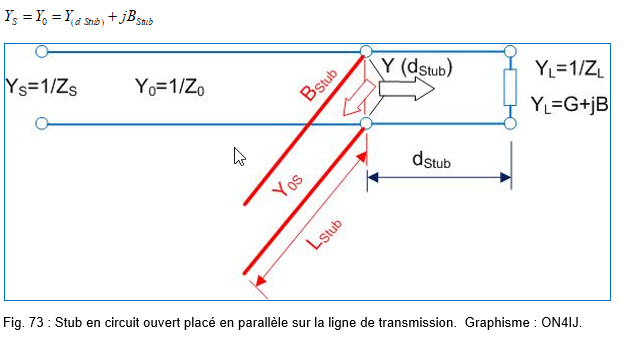
Pour que la charge soit adaptée à la source, il faut que la susceptance du Stub annule celle qui est présente à la distance d_Stub, c’est-à-dire :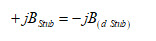

En général, on choisit pour des raisons pratiques une impédance caractéristique du segment de ligne formant le Stub à la même valeur que celle de la ligne de transmission principale : Z_0S = Z₀. Les radioamateurs utilisent en général un Stub parallèle sur des lignes coaxiales car le raccordement de celui-ci est plus commode : il suffit d’utiliser un connecteur en « TÉ ».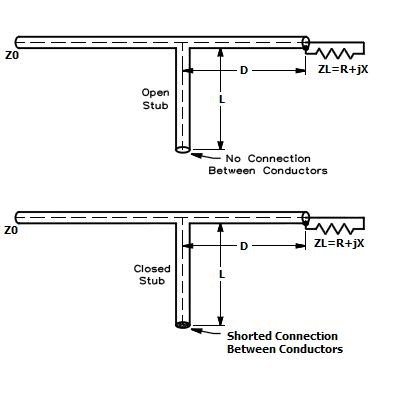

Fig. 74 : Stub en circuit ouvert ou en court-circuit sur une ligne coaxiale. Source Martin Storli LA8OAK.

En pratique, on préfère utiliser un Stub en court-circuit lorsqu’on utilise des lignes coaxiales car il est difficile d’aménager un circuit ouvert parfait sans rayonnement parasite. Toutefois, lorsqu’un circuit électronique UHF ou SHF est conçu sur un circuit imprimé où les lignes de transmission entre étages sont réalisées en technique « micro ruban » (Micro Strip), on préfère utiliser un Stub en circuit ouvert car cela évite de devoir placer des trous métallisés entre les couches (entre les deux faces) du circuit imprimés pour former un court-circuit.
Quelle est la longueur d’un Stub en court-circuit avec un câble coaxial RG213U devant présenter une inductance de 87,81 nH à la fréquence de 145 MHz ?
L’inductance normalisée est :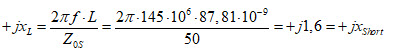

Par calcul analytique, la longueur du Stub est :

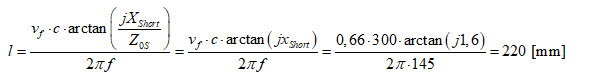
Voyons le même calcul sur l’abaque de Smith :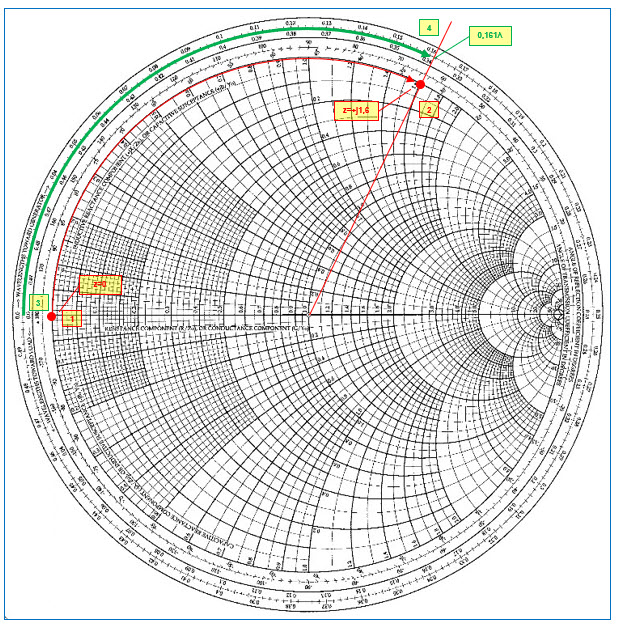

Fig. 75 : Calcul de la longueur d’un Stub en court-circuit d’inductance normalisée de +j1,6. Graphisme : ON4IJ.

Un court-circuit correspond à une impédance normalisée de z = 0 située au point (1). Pour arriver à une inductance normalisée de +j1,6 on se déplace dans le sens horlogique (Toward Generator) sur le cercle à résistance constante du périmètre de l’abaque jusqu’à une impédance normalisée de +j1,6 située au point (2). Traçons une droite partant du centre de l’abaque et passant par le point d’impédance +j1,6. Sur l’échelle des longueurs d’onde vers la source (Wavelengths Toward Generator), en partant de 0λ situé au point (3) en face du point (1), nous arrivons à une longueur d’onde de 0,161λ au point (4). La longueur du Stub de 0,161λ électrique à 145 MHz est donc de :

Le tracé sur l’abaque de Smith à la figure 76 est similaire à celui de la figure 75 mais cette fois le déplacement s’effectue du point (1) d’impédance normalisée z = 0 jusqu’au point (2) d’impédance normalisée -j1,6.
Sur l’échelle des longueurs d’onde vers la source (Wavelengths Toward Generator), en partant de 0λ situé au point (3) en face du point (1), nous arrivons à une longueur d’onde de 0,339λ au point (4). La longueur du Stub de 0,339λ électrique à 145 MHz est donc de :

On remarquera que la longueur d’onde électrique est comprise entre λ/4 et λ/2 (capacitance).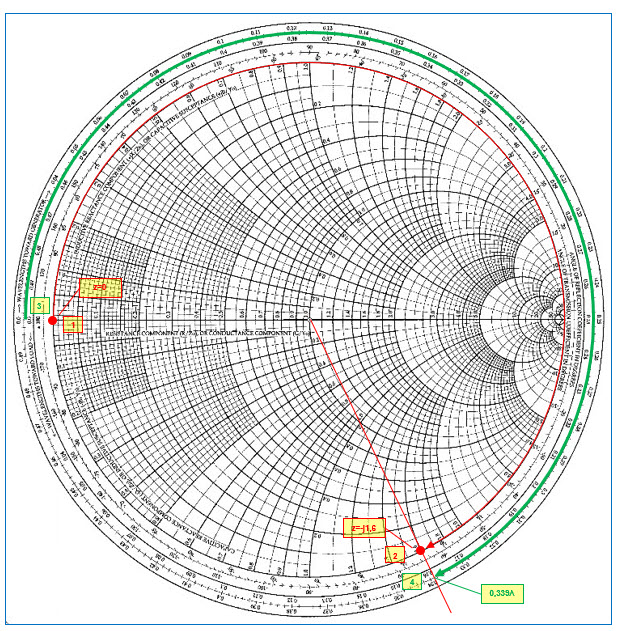

Fig. 76 : Calcul de la longueur d’un Stub en court-circuit de capacitance normalisée de -j1,6. Graphisme : ON4IJ.

Quelle est la longueur d’un Stub en circuit ouvert avec un câble coaxial RG213U devant présenter une inductance de 87,81 nH à la fréquence de 145 MHz ?

L’inductance normalisée est :

Voyons le même calcul sur l'abaque de Smith
Un circuit ouvert correspond à une impédance normalisée de z = ∞ située au point (1). Pour arriver à une inductance normalisée de +j1,6 on se déplace dans le sens horlogique (Toward Generator) sur le cercle à résistance constante du périmètre de l’abaque jusqu’à une impédance normalisée de +j1,6 située au point (2). Traçons une droite partant du centre de l’abaque et passant par le point d’impédance +j1,6. Sur l’échelle des longueurs d’onde vers la source (Wavelengths Toward Generator), en partant de 0,25λ situé au point (3) en face du point (1), en passant par 0,5λ, nous arrivons à une longueur d’onde de 0,161λ au point (4). La longueur du Stub est de (0,5λ-0,25λ)+0,161λ = 0,411λ électrique à 145 MHz est donc de :

On remarquera que la longueur d’onde électrique est comprise entre λ/4 et λ/2 (inductance).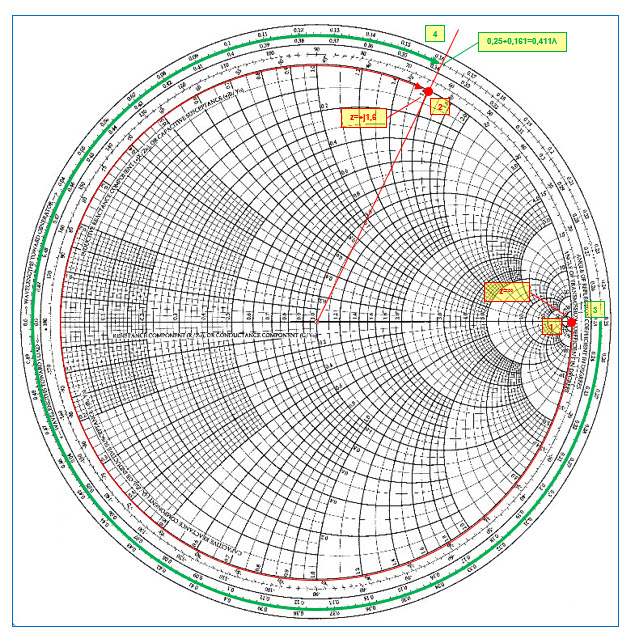

Fig. 77 : Calcul de la longueur d’un Stub en circuit ouvert d’inductance normalisée de +j1,6. Graphisme : ON4IJ.

Quelle est la longueur d’un Stub en circuit ouvert avec un câble coaxial RG213U devant présenter une capacitance de 13,72 pF à la fréquence de 145 MHz ?

La capacitance normalisée est :

Le tracé sur l’abaque de Smith à la figure 78 est similaire à celui de la figure 77 mais cette fois le déplacement s’effectue du point (1) d’impédance normalisée z = 0 jusqu’au point (2) d’impédance normalisée -j1,6.

Sur l’échelle des longueurs d’onde vers la source (Wavelengths Toward Generator), en partant de 0,25λ situé au point (3) en face du point (1), nous arrivons à une longueur d’onde de 0,339λ au point (4). La longueur du Stub de 0,339λ-0,25λ = 0,089λ électrique à 145 MHz est donc de :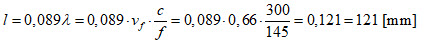

On remarquera que la longueur d’onde électrique est inférieure à λ/4 (capacitance).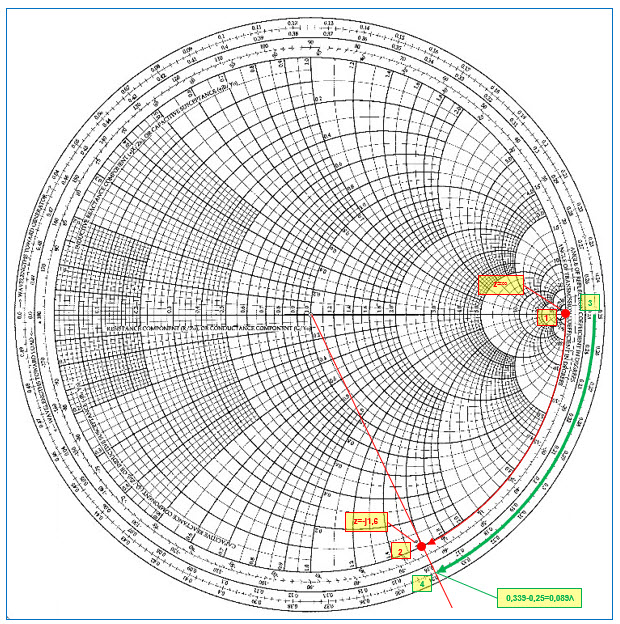

Fig. 78 : Calcul de la longueur d’un Stub en circuit ouvert de capacitance normalisée de -j1,6. Graphisme : ON4IJ.

En ce qui concerne la mise en parallèle d’un Stub, la méthode de calcul analytique et le tracé sur l’abaque de Smith est similaire à ce qui a été décrit ci-dessus pour les réactances sauf qu’il faut raisonner en susceptances. La susceptance du stub est située sur un point diamétralement opposé au point de réactance sur l’abaque. Ainsi, pour un Stub en court-circuit z = 0 et y = ∞ ; pour un Stub en circuit ouvert, z = ∞ et y = 0.

En récapitulant les résultats, des quatre exemples décrits ci-dessus, on constate qu’il y a deux solutions pour une inductance et deux solutions pour une capacitance : soit on choisit un Stub en court-circuit, soit on choisit un Stub en circuit ouvert pour arriver à la réactance voulue. Selon le cas de figure, il est préférable de choisir la solution qui donne une longueur de Stub la plus courte afin de diminuer les pertes.

Comme nous maîtrisons à présent non seulement le calcul d’une impédance dans une ligne de transmission à une certaine distance de la charge mais aussi le calcul de la longueur d’un Stub pour une réactance (ou susceptance) donnée, nous pouvons réaliser l’adaptation d’une charge à une ligne de transmission au moyen d’un Stub.

Cas pratique d’adaptation par simple Stub :

Soit une antenne qui présente à ses bornes une impédance complexe de Z_L = 100+j80 Ω à une fréquence de travail de 145 MHz. Le Feeder d’antenne est un câble coaxial RG213U d’impédance caractéristique de 50 Ω. On veut réaliser une adaptation par un Stub en parallèle sur la ligne. Le Stub est réalisé avec le même câble coaxial que celui de la ligne de transmission. À quelle distance de l’antenne doit se situer ce Stub ? Quelle doit être la longueur du Stub si celui-ci est du type en court-circuit ? Quelle doit être la longueur du Stub si celui-ci est du type en circuit ouvert ?

L’impédance normalisée de l’antenne est z_L = 100/50+j80/50 = 2+j1,6. Plaçons cette impédance sur l’abaque au point (1), voir figure 79. Comme nous voulons placer un Stub en parallèle, on va situer le point d’admittance de l’antenne au point (2) y_L = 0,305‑j0,244 diamétralement opposé au point (1). Traçons une droite partant du centre de l’abaque et passant par le point (2). Le prolongement de cette droite sur l’échelle des longueurs d’ondes vers la source (Toward Generator) donne une valeur au point (3) de 0,459λ. Traçons un cercle à SWR constant passant par le point d’impédance de l’antenne (passant donc aussi par son point d’admittance). Le SWR de l’antenne est de 3,42:1 qui est lu sur la partie droite de l’axe X des résistances pures ou en reportant la longueur du rayon sur l’échelle radiale « SWR ».

Le cercle à SWR constant intercepte le cercle à résistance constante unitaire (qui représente le cercle à conductance constante unitaire) en deux points. Cela signifie qu’il y a deux possibilités de distance par rapport à la charge pour placer un Stub : au point (4) d’impédance z_{(d Stub A)} = 1+j1,32 et au point (5) d’impédance z_{(d Stub B)} = 1-j1,32.
Traçons une première droite partant du centre de l’abaque et passant par le point (4) et une deuxième droite partant du centre et passant par le point (5). Le prolongement de la droite passant par le point (4) donne sur l’échelle des longueurs d’onde vers la source une valeur au point (6) de 0,172λ : position (A) pour le Stub ; le prolongement passant par le point (5) donne une valeur au point (7) de 0,328λ : position (B) pour le Stub.

Pour la position (A) du Stub, on se déplace d’un angle θ₁ à partir du point (3) de 0,459λ vers le point (6) de 0,172λ en passant par 0,5λ. L’amplitude du déplacement θ₁ correspond à une distance de la charge de (0,5λ-0,459λ)+0,172λ = 0,213λ = N_λA.

Pour la position (B) du Stub, on se déplace d’un angle θ₂ à partir du point (3) de 0,459λ vers le point (7) de 0,328λ en passant par 0,5λ. L’amplitude du déplacement θ₂ correspond à une distance de la charge de (0,5λ-0,459λ)+0,328λ = 0,369λ = N_λB.

La distance entre l’antenne et la position (A) du Stub est de :

Il nous reste à calculer la longueur du Stub en court-circuit ou en circuit ouvert à placer en position (A) ou en position (B) par la méthode analytique et par l’abaque de Smith.
En position (A), l’impédance lue au point (4) correspond à l’admittance présente dans la ligne de transmission : y_{(d Stub A)} = 1+j1,32.

Pour annuler la susceptance de b_(d Stub A) = +j1,32 un Stub en court-circuit devra présenter une susceptance de ‑b_(d Stub A) = b_(Stub A) = ‑j1,32 et sa longueur devra être de :

Sur l’abaque de Smith le calcul de la longueur d’un Stub en court-circuit et placé en parallèle sur une ligne de transmission est tel qu’à l’extrémité du Stub z = 0 et donc y = ∞. Plaçons le point (8) y= ∞ (sur la droite l’abaque).

Comme nous avons démarré le tracé sur l’abaque de Smith à partir de l’admittance de la charge au point (2), les tracés sur les réseaux de cercles sont des impédances lues représentant des admittances. Il est toutefois possible de travailler directement sur les réseaux des cercles miroités de l’abaque d’admittance et ceux d’impédance (imittance) pour le tracé complet de la résolution du calcul.
Longueur d’un Stub en court-circuit en position (A) :

La susceptance du Stub placé en (A) doit être de : b_(Stub A) = ‑j1,32. Repérons le cercle à réactance constante lue de -j1,32 qui justement passe par le point (5). Suivons cet arc de cercle à réactance constante lue de -j1,32 jusqu’au périmètre de l’abaque au point (11) et prolongeons son extrémité par un segment de droite (rayon) jusqu’à l’échelle des longueurs d’onde vers la source (Toward Generator) au point (12) qui nous donne l’indication de 0,353λ. Le déplacement sur l’abaque pour ce Stub s’effectue à partir du point (8) où y = ∞ (où nous pouvons lire l’indication de 0,25λ) jusqu’au point (12). La longueur du Stub est donc de 0,353λ-0,25λ = 0,103λ. La longueur réelle du Stub sera de :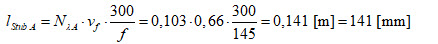

Longueur d’un Stub en court-circuit en position (B) :

La susceptance du Stub placé en (B) doit être de : b_(Stub A) = +j1,32. Repérons le cercle à réactance constante lue de +j1,32 qui justement passe par le point (4). Suivons cet arc de cercle à réactance constante lue de +j1,32 jusqu’au périmètre de l’abaque au point (9) et prolongeons son extrémité par un segment de droite (rayon) jusqu’à l’échelle des longueurs d’onde vers la source (Toward Generator) au point (10) qui nous donne l’indication de 0,147λ. Le déplacement sur l’abaque pour ce Stub s’effectue à partir du point (8) où y = ∞ (où nous pouvons lire l’indication de 0,25λ) jusqu’au point (10) en passant par la valeur 0,5λ. La longueur du Stub est donc de (0,5λ-0,25λ)+0,147λ = 0,397λ. La longueur réelle du Stub sera de :

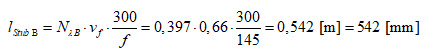
Longueur d’un Stub en circuit ouvert :
Le raisonnement est similaire à celui décrit ci-dessus sauf que les déplacements sur l’échelle des longueurs d’onde vers la source pour le calcul de la longueur du Stub en circuit ouvert s’effectuent à partir du point (13) où y = 0 (z = ∞).
Longueur d’un Stub en circuit ouvert en position (A) :

Voyons tout cela sur l’abaque de Smith à la figure 79 suivante.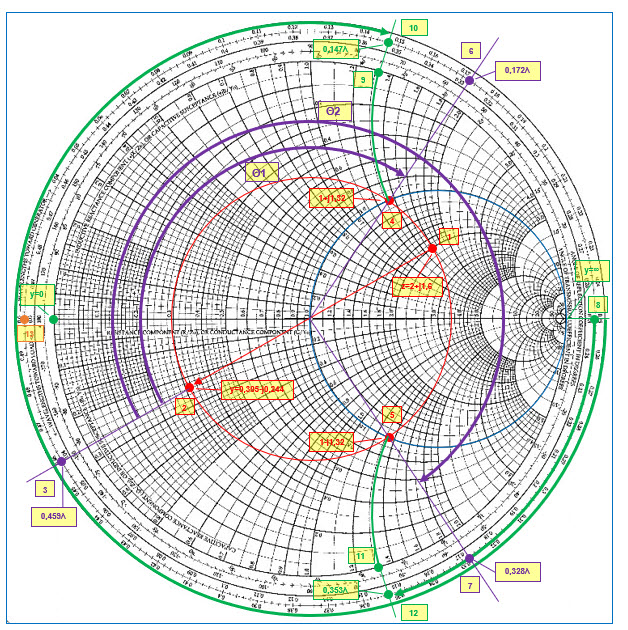

Fig. 79 : Calcul de la distance par rapport à la charge et de la longueur d’un Stub en parallèle sur une ligne de transmission RG213U pour adapter une antenne d’impédance complexe de 100+j80 Ω à une fréquence de travail de 145 MHz. Pour le calcul de la longueur d’un Stub en court-circuit : partir du point (8) vers les points (12) ou (10). Pour le calcul de la longueur d’un Stub en circuit ouvert : partir du point (13) vers les points (10) ou (12). Graphisme : ON4IJ.

En un seul coup d’œil sur l’abaque de Smith on peut visualiser, selon les déplacements sur celle-ci, quelle sera la distance la plus courte par rapport à la charge pour placer un Stub et quelle sera la longueur minimale du Stub à choisir parmi les types de terminaison : en court-circuit ou en circuit ouvert.

Meilleur compromis : Stub « Short », longueur 141 mm et à 291 mm de la charge.

Adaptation par double Stub :

Dans ce qui a été décrit ci-dessus, on constate que l’adaptation par simple Stub présente une contrainte de positionnement de celui-ci à une distance critique de la charge. Il serait plus commode d’obtenir un système d’adaptation sans contrainte de distance de positionnement. Dans un système d’adaptation par double Stub, il est possible de choisir une distance arbitraire à partir de la charge pour le placement d’un premier Stub et il est aussi possible de choisir une autre distance arbitraire entre le premier et deuxième Stub. L’adaptation s’effectue en calculant la longueur des deux Stubs. Certains systèmes d’adaptation par double Stub disposent d’un réglage de longueur de ceux-ci de manière à adapter des charges d’une gamme d’impédances différentes.
Une fois que la distance entre la charge et le premier Stub est choisie, l’impédance à adapter ne doit pas se situer dans une zone d’exclusion (zone interdite) de l’abaque de Smith. Si tel est le cas, alors, tout en conservant la même distance entre les deux Stubs, il y a lieu de choisir une autre distance entre le premier Stub et la charge pour sortir de cette zone interdite. Nous examinerons ces zones interdites par la suite. Si les conditions de mise en œuvre de deux Stubs à des distances déterminées ne permettent pas d’adapter l’impédance de la charge, alors on peut toujours avoir recours à un troisième Stub qui donnera une solution d’adaptation quelle que soit l’impédance de la charge sans modification de distance entre la charge et le premier Stub ni de modification de distance entres les trois Stubs.

Cas pratique d’adaptation par double Stub :
Soit une antenne qui présente à ses bornes une impédance complexe de Z_L = 10+j15 Ω à une fréquence de travail de 145 MHz. Le Feeder d’antenne est un câble coaxial RG213U d’impédance caractéristique de 50 Ω. On veut réaliser une adaptation par double Stub chacun en court-circuit et placés en parallèle sur la ligne. Les Stubs sont réalisés avec le même câble coaxial que celui de la ligne de transmission. On demande de choisir une distance entre la charge et le premier Stub et on demande de choisir une distance entre les deux Stubs. Quelle sera la longueur de chaque Stub ?
Comme les Stubs sont en parallèle sur la ligne, on va travailler en admittance sur l’abaque de Smith. Plaçons l’impédance normalisée z_L=0,2+j0,3 de la charge au point (1) et son admittance normalisée y_L = 1,5‑j2,3 diamétralement opposée au point (2). Traçons le cercle à SWR constant passant par les points (1) et (2) et dont la longueur du rayon donne une valeur de SWR de 5,6:1. Traçons une droite partant du centre de l’abaque et passant par le point (2). Le prolongement de cette droite sur l’échelle des longueurs d’ondes vers la source (Toward Generator) donne une valeur au point (3) de 0,2985λ.
Choisissons une distance entre la charge et le premier Stub d’un déplacement de 0,1λ ce qui correspond à une longueur de ligne de transmission de :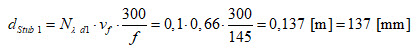

Ce déplacement s’effectue sur l’échelle des longueurs d’onde vers la source (Toward Generator) : du point (3) on arrive au point (4) 0,2985λ+0,1λ = 0,3985λ. L’impédance lue sur le cercle à SWR constant après le déplacement de 0,1λ est de 0,29-j0,7 au point (5). Le premier Stub placé à cet endroit aura pour effet un déplacement sur un cercle à résistance constante lue de 0,29 correspondant à une conductance constante.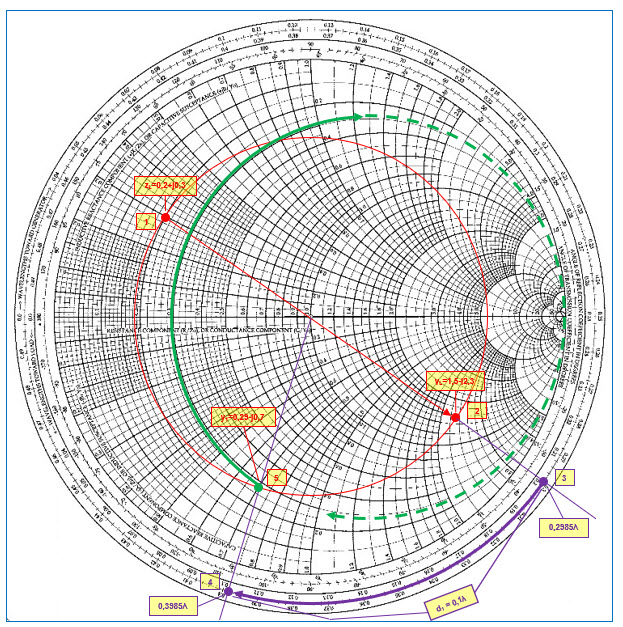

Fig. 80 : Déplacement de 0,1λ à partir de la charge jusqu’à l’emplacement du premier Stub. L’effet du premier Stub sera un déplacement sur un cercle à résistance lue constante (conductance constante) dans le sens horlogique. Graphisme : ON4IJ.

Maintenant, sur la figure 80, où aller à partir du point (5) sur le cercle de couleur verte à résistance lue constante de 0,29 pour déterminer la longueur du premier Stub ?

Nous voudrions arriver quelque part sur l’abaque de Smith de telle manière que par la suite en se déplaçant de la distance entre les deux Stubs on parvienne en fin de compte sur un cercle à résistance constante lue unitaire. Si on parvient à se situer sur ce cercle unitaire à l’emplacement de la ligne de transmission où sera positionné le deuxième Stub, alors l’effet de celui-ci nous ramènera au centre de l’abaque pour que le tour soit joué et que l’adaptation soit parfaite.
C’est à partir de maintenant que les choses deviennent subtiles et que nous demandons au lecteur toute son attention pour bien comprendre ce qui suit.
Appelons la position (A) à l’emplacement où est situé le premier Stub et appelons la position (B) à l’emplacement où sera situé le deuxième Stub, voir figure 81.
Choisissons un écart entre les deux Stubs de 0,15λ. La distance entre la position (A) et la position (B) est donc S = 0,15λ :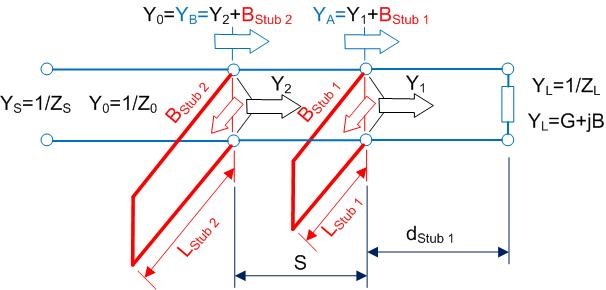

Fig. 81 : Placement des deux Stubs : 1^er Stub à une distance d_{Stub 1} de la charge ; écart entre les deux Stubs à une distance S entre eux ; 1^er Stub placé en position (A) ; 2^ème Stub placé en position (B). Graphisme : ON4IJ.

Si nous voulons trouver un point sur l’abaque de Smith à partir duquel un déplacement de (A) vers (B) vers la source nous amène sur le cercle à résistance constante lue unitaire, cela revient à faire pivoter ce cercle unitaire de (B) vers (A) en direction de la charge. Faire pivoter le cercle unitaire revient à lui faire subir une rotation en direction de la charge (Toward Load) en ayant pour point de pivot le centre de l’abaque.
L’angle de rotation du cercle unitaire s’effectue sur l’échelle des longueurs d’onde en direction de la charge. L’amplitude de rotation exprimée en longueur d’onde électrique correspond à la distance S entre la position (B) et la position (A) de la ligne de transmission.
Ainsi, si on fait pivoter le cercle unitaire en lui faisant subir une rotation de S = 0,15λ (écart entre les deux Stubs) en direction de la charge, alors, n’importe quel point situé sur le cercle unitaire pivoté va nous garantir de revenir sur le cercle unitaire d’origine lorsqu’on reviendra en direction de la source en effectuant le déplacement de la distance S de 0,15λ.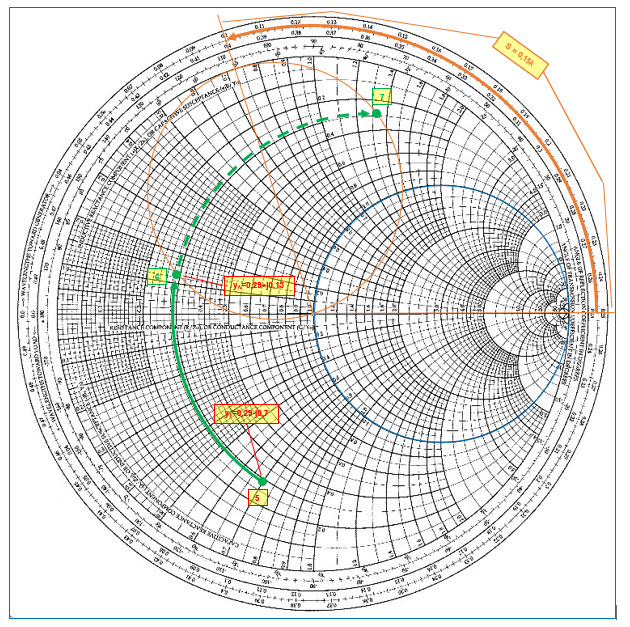

Fig. 82 : Le cercle unitaire est pivoté et subit une rotation lue sur l’échelle des longueurs d’onde en direction de la charge. La rotation correspond à l’écart en longueur d’onde entre les deux Stubs : 0,4λ‑0,25λ = 0,15λ. Graphisme : ON4IJ.

Il y a deux possibilités de susceptance pour le calcul de la longueur du premier Stub : du point (5) vers le point (6) ou bien du point (5) vers le point (7).

Sur le tracé sur l’abaque de Smith à la figure 82 on peut observer que le trajet pour passer du point (5) vers le point (6) est plus court que celui du point (5) vers le point (7) et c’est cette solution que nous allons retenir car elle donnera un résultat de calcul d’une longueur plus courte ; il y aura donc moins de pertes dans le Stub. Pour passer du point (5) au point (6), nous sommes partis d’une impédance y₁ = 0,29-j0,7 vers une impédance de y_A = 0,29+j0,13 ce qui donne une variation de susceptance de +j0,13‑(‑j0,7) = +j0,83.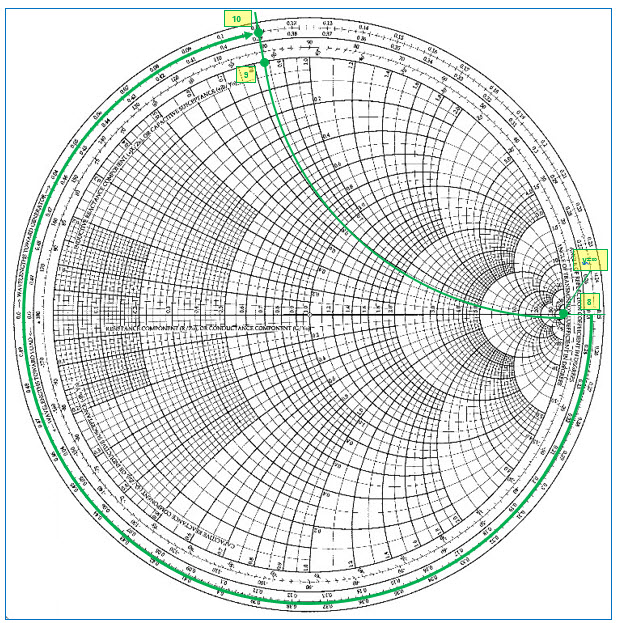

Fig. 83 : Calcul de la longueur du premier Stub en court-circuit et en parallèle sur la ligne. La susceptance du Stub doit être de +j0,83. Graphisme : ON4IJ.

Pour le calcul de la longueur d’un Stub parallèle en court-circuit on part du point de l’abaque où y = ∞ situé au point (8) de la figure 83 donnant une lecture de 0,25λ sur la droite de l’abaque (en travaillant en admittance sur l’abaque) et on se déplace dans le sens horlogique sur l’échelle des longueurs d’onde vers la source (Toward Generator) jusqu’au point (9) de la susceptance que le Stub doit amener : ici +j0,83.

La lecture au point (10) donne une valeur de 0,1105λ. La longueur d’onde électrique du Stub sera donc de (0,5λ-0,25λ)+0,1105λ = 0,3605λ. La longueur du premier Stub sera :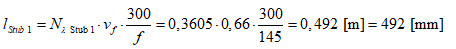

Nous étions arrivé au point (6) sur la figure 82 dont l’impédance lue est y_A = 0,29+j0,13. Sur la figure 84, nous allons à présent nous déplacer sur la ligne de transmission de la distance S = 0,15λ entre la position (A) du premier Stub au point (11) de 0,022λ vers la position (B) du deuxième Stub au point (12) de 0,022λ+0,15λ = 0,172λ. Le déplacement s’effectue sur un cercle à SWR constant de 3,4:1 et passant par le point (6).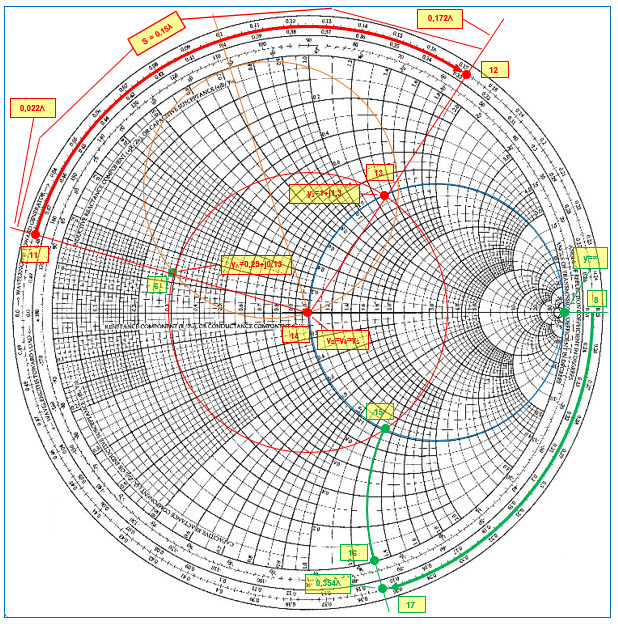

Fig. 84 : Déplacement de la position (A) à la position (B) de S = 0,15λ et calcul de la longueur du deuxième Stub. Graphisme : ON4IJ.

Du point (6) en se déplaçant de S = 0,15λ nous arrivons pile au point (13) sur le cercle unitaire (en bleu) sur l’abaque où l’impédance lue (représentant une admittance) est y₂ = 1+j1,3. La susceptance du deuxième Stub va devoir annuler celle de y₂ et donc devra avoir une valeur de -j1,3 pour atteindre le centre de l’abaque au point (14). Ce point représente l’admittance y_B = y₀ = y_S = 1+j0. L’adaptation est donc parfaite à 50 Ω.

Pour calculer la longueur du deuxième Stub de susceptance de -j1,3 au point (15) et au point (16) on part du point (8) où y = ∞ et on se déplace sur l’échelle des longueurs d’onde dans le sens horlogique vers la source (Toward Generator) jusqu’au point (17) où nous pouvons lire une valeur de 0,354λ. La longueur d’onde électrique du Stub sera donc de 0,354λ-0,25λ = 0,104λ. La longueur du deuxième Stub sera :

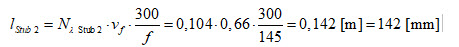
Dans ce que nous venons d’effectuer comme tracés sur l’abaque de Smith, il y a lieu de bien distinguer d’une part les déplacements sur des cercles à SWR constant lorsqu’on se déplace le long de la ligne de transmission à partir de la charge vers la source jusqu’au premier Stub ou jusqu’au deuxième Stub et d’autre part les déplacements sur des cercles à résistance ou conductance constante lorsqu’il s’agit d’amener au réseau adaptateur une réactance ou une susceptance.
Lorsqu’on a effectué le déplacement sur la ligne de transmission à partir de la charge jusqu’à la position du premier Stub, on arrive à une point d’impédance lue (représentant ici une admittance) situé sur l’abaque de Smith. C’est à partir de ce point que l’on effectue un déplacement sur un cercle à résistance lue (ou conductance) qui doit impérativement intercepter le cercle unitaire pivoté d’une rotation correspondant à la distance S entre les deux Stubs ; voir déplacement entre le point (5) et le point (6) sur la figure 82.
En observant bien l’abaque de Smith, nous pouvons constater qu’en fonction de la position du cercle unitaire pivoté d’une rotation correspondant à la distance S entre les deux Stubs, il y a toute une série de cercle à résistance constante qui n’interceptent pas le cercle unitaire pivoté comme nous allons l’observer sur les figures suivantes. Si le point d’impédance (ou d’admittance) qui est présente sur la ligne de transmission à la position du premier Stub se situe à l’intérieur d’un de ces cercles qui n’intercepte pas le cercle unitaire pivoté, alors il n’y a pas de solution compatible pour l’adaptation. Le point d’impédance se situe dans une zone interdite sur l’abaque de Smith.
Si l’écart entre les Stubs est déjà fixé, alors il faut modifier la distance entre la charge et le premier Stub pour pouvoir sortir de la zone interdite en se déplaçant sur un cercle à SWR constant. Si toutes les distances sont déjà fixées et qu’elles ne peuvent pas être changées, alors il faut mettre en œuvre un troisième Stub pour pouvoir solutionner l’adaptation entre la charge et la source.

En général, on choisit la distance d’écart entre les deux Stubs correspondant à une fraction de longueur d’onde électrique de la ligne de transmission parmi les valeurs suivantes :

S = λ/4 ; S = 3λ/4 ; …

S = 3λ/16 ; S = 5λ/16 ; …

S = λ/8 ; S = 3λ/8 ; …

S = λ/16 ; S = 7λ/16 ; ...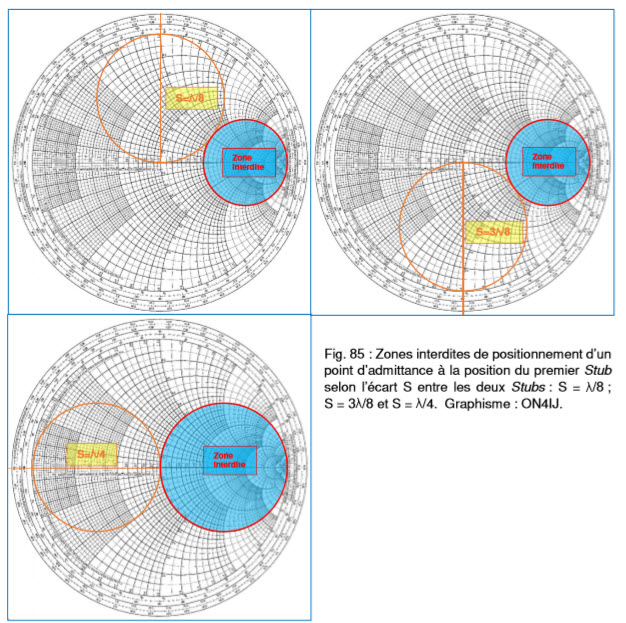

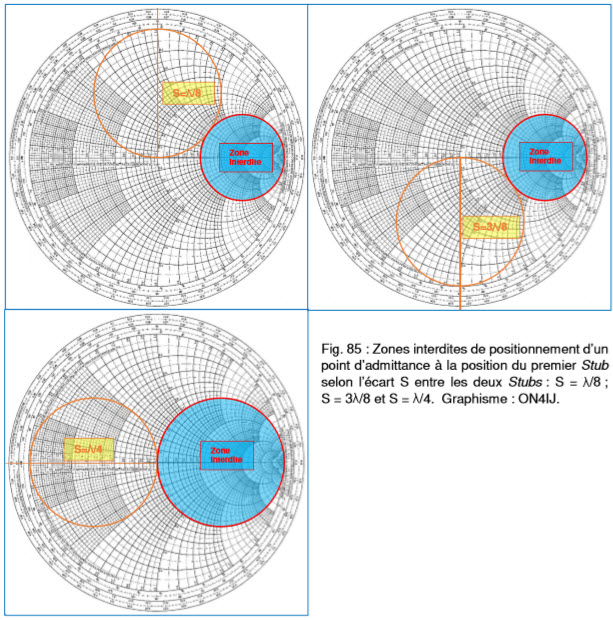
Maintenant que nous avons compris le principe des zones interdites en fonction de la distance d’écart S entre les deux Stubs, on peut résumer celles-ci sur la figure à la page suivante. Sur la partie de droite se situent les zones interdites pour les points d’admittance comme illustrés ci-dessus. Sur la figure suivante on peut observer les zones interdites des points d’admittance à droite et les zones interdites des points d’impédance situés à gauche de l’abaque de Smith (voir figure 87).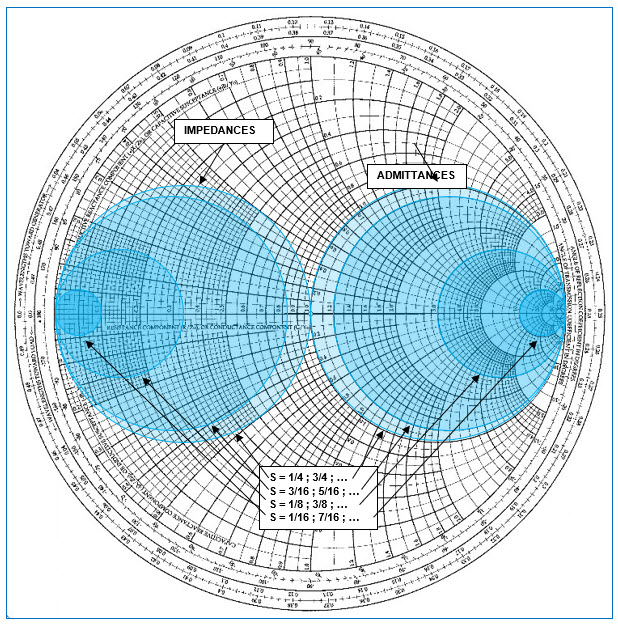

Fig. 87 : Zones interdites de positionnement d’un point d’impédance (à gauche) ou d’admittance (à droite) à la position du premier Stub selon l’écart S entre les deux Stubs. Graphisme : ON4IJ.

Il y aurait encore beaucoup à dire sur l’adaptation par Stub qui est largement utilisée sur les circuits imprimés des circuits électroniques en SHF. Certains Stubs sont d’une impédance différente de celle de la ligne de transmission pour être plus court ou pour offrir une plus grande largeur de bande passante sur le circuit. Enfin, il est possible d’utiliser au même emplacement deux Stubs en parallèle pour additionner leur susceptance. On retrouve cette technique dans les « Balanced Matching Stub » des circuits micro-ondes. Cela permet entre autres d’optimiser l’encombrement des Stubs sur un circuit imprimé.

Adaptation par trois Stubs :

Une pratique souvent employée en ce qui concerne une adaptation universelle par trois Stubs est de choisir un écart entre chaque Stub de S = 3λ/8. Les trois Stubs sont raccordés en parallèle sur la ligne de transmission.

Pour simplifier le calcul et donc le réglage d’un tel dispositif, on choisit d’effectuer l’adaptation par les deux premiers Stubs (1 & 2) ou les deux derniers Stubs (2 & 3) comme cela a été décrit ci-dessus pour une adaptation par deux Stubs. Le 3^ème Stub ou le 1^er Stub selon le cas est donc « inutilisé » pour l’adaptation mais cela ne veut pas dire qu’il est déconnecté : il est tout simplement accordé sur un quart d’onde en court-circuit et devient ainsi complètement transparent au système, c’est-à-dire qu’il ne participe plus à l’adaptation car il ne présente aucune susceptance. En effet, un quart d’onde en court-circuit à une extrémité présente une impédance infinie à l’autre extrémité.

Réaliser une adaptation sur les deux premiers Stubs ou les deux derniers Stubs revient tout simplement à « modifier » la distance entre la charge et le « premier » Stub rencontré et participant à l’adaptation : selon le cas, cette distance est celle entre la charge et le 1^er Stub ou bien entre la charge et le 2^ème Stub. Ainsi, il est possible de sortir de la zone interdite de l’admittance par cette astucieuse « modification » de la distance entre la charge et le « premier » Stub rencontré participant à l’adaptation. Rien ne doit être changé physiquement aux raccordements à la ligne de transmission.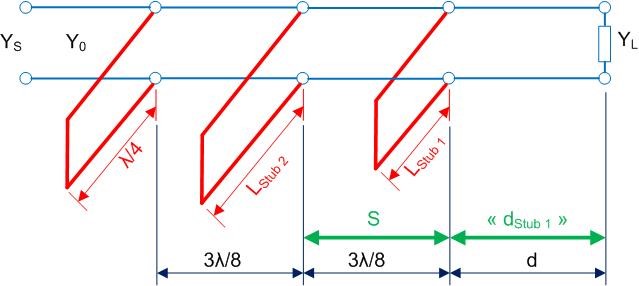

Fig. 88 : Adaptation par le 1^er et 2^ème Stub avec une distance d_{Stub 1} = d et S = 3λ/8. Le 3^ème Stub de λ/4 n’exerce aucun effet et se comporte comme un isolant parfait au niveau de la ligne de transmission. Graphisme : ON4IJ.

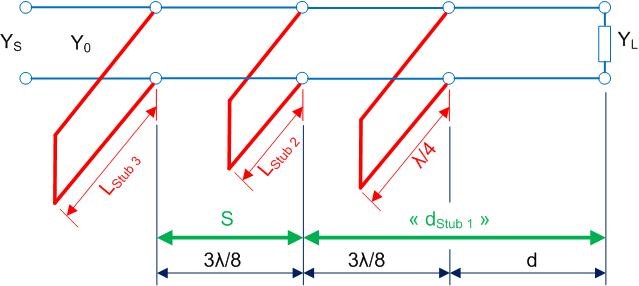
Fig. 89 : Adaptation par le 2^ème et 3^ème Stub avec une distance d_{Stub 1} = (d + 3λ/8) et S = 3λ/8. Le 1^er Stub de λ/4 n’exerce aucun effet et se comporte comme un isolant parfait au niveau de la ligne de transmission. Graphisme : ON4IJ.

Adaptation d’impédance par un transformateur quart d’onde :

L’adaptation entre une charge et une source par un transformateur quart d’onde (QWT : Quarter Wave Transformer) est bien connue des radioamateurs. Il suffit de trouver une ligne de transmission d’une longueur de λ/4 dont l’impédance caractéristique est la moyenne géométrique entre l’impédance de la charge et celle de la source.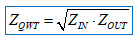

Il y a toutefois une condition essentielle pour pouvoir utiliser un adaptateur quart d’onde : l’impédance de la charge doit être purement résistive.

En revanche, il y a toujours moyen de transformer une charge présentant une partie réactive en une impédance résistive pure : il suffit de placer un segment de ligne de transmission dont la longueur est calculée pour résorber la partie réactive de la charge ; voir figure ci-dessous.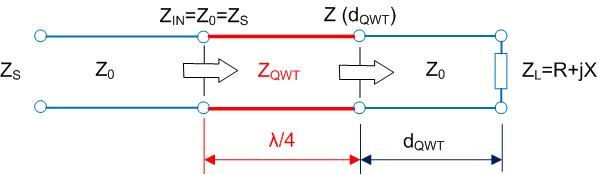

Fig. 90 : Adaptation par segment de ligne et transformateur quart d’onde lorsque la charge présente une partie réactive. Graphisme : ON4IJ.

Exemple d’adaptation par transformateur quart d’onde et segment de ligne de transmission pour une charge réactive :

Soit une antenne d’impédance de 150+j100 Ω que l’on veut adapter à une source de 50 Ω à une fréquence de travail de 145 MHz. La ligne de transmission est constituée d’un câble coaxial RG313U. Quelle sera la longueur du segment de ligne de transmission pour résorber la partie réactive de l’antenne ? Quelle sera l’impédance caractéristique du transformateur quart d’onde ?

L’impédance normalisée de la charge dans un système 50 Ω (impédance de la source et celle de la ligne de transmission principale) est 150/50+j100/50 = 3+j2. Plaçons cette impédance au point (1) sur l’abaque de Smith ; voir figure 91. Traçons une droite partant du centre de l’abaque et passant par le point d’impédance normalisée de la charge. Prolongeons cette droite jusqu’au périmètre de l’abaque sur l’échelle des longueurs d’onde en direction de la source (Toward Generator). La lecture nous donne 0,224λ.

Traçons un cercle à SWR constant jusqu’à ce qu’il intercepte l’axe des résistances pures au point (2) ; le SWR a ici une valeur de 4,4:1. Nous nous sommes déplacé sur un segment de ligne de transmission en direction de la source de 0,224λ jusqu’à 0,25λ. La longueur d’onde électrique de ce segment est de 0,25λ-0,224λ = 0,026λ. La longueur du segment de ligne 50Ω directement raccordé à l’antenne aura pour longueur :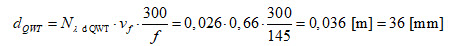

Si cette distance est incompatible pour le raccordement de ce segment relativement court, on peut toujours rajouter une longueur électrique de λ/2 car la même impédance se répète tous les λ/2 le long d’une ligne de transmission ; cela correspond à effectuer un tour complet sur un cercle à SWR constant sur l’abaque de Smith. Dans ce cas, la longueur serait :

Plaçons cette nouvelle impédance au point (3) sur l’abaque et traçons un cercle à SWR constant passant par ce point d’impédance de 2,09+j0. Maintenant nous nous déplaçons dans le sens horlogique (Toward Generator) de λ/4 = 0,25λ vers la source pour arriver au point (4) d’impédance de z_IN = 0,4785+j0. Ce que nous venons de faire à l’instant est de se déplacer de la sortie vers l’entrée du segment de ligne de transmission d’impédance de 105 Ω et d’une longueur de 0,25λ formant le transformateur quart d’onde. Il faut maintenant retrouver l’impédance réelle à l’entrée du quart d’onde :

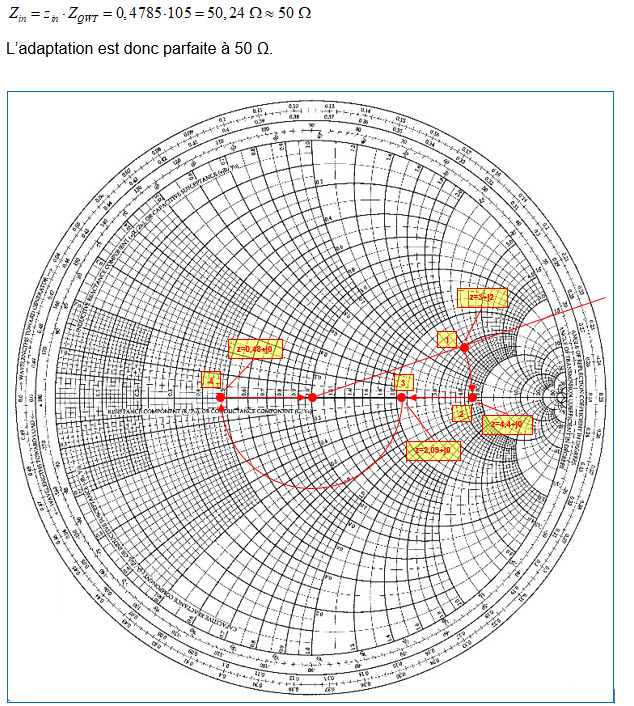
Fig. 91 : Adaptation d’une charge qui présente une partie réactive avec un segment de ligne et un transformateur quart d’onde. Graphisme : ON4IJ.

Remarque : on aurait très bien pu choisir un segment de ligne de 150 Ω entre l’antenne et le quart d’onde ; la normalisation de l’impédance à l’antenne et à l’entrée du segment de ligne aurait été effectuée en fonction de cette impédance caractéristique de ligne. On peut même envisager n’importe quelle impédance caractéristique pour ce segment de ligne. Cela nous aurait amené une autre valeur d’impédance résistive pure à la sortie du quart d’onde et celui-ci même aurait été d’une autre impédance caractéristique. On constate que quelques tracés sur l’abaque peuvent nous orienter vers des valeurs les plus proches des impédances des lignes de transmission commerciales.
Le transformateur quart d’onde est parfois intéressant pour raccorder plusieurs antennes identiques et en phase sur une même ligne de transmission. C’est ce que font les radioamateurs en VHF ou en UHF pour raccorder deux ou quatre antennes Yagi, chacune d’impédance de 50 Ω sur un même Feeder de 50 Ω. Le signal venant de l’émetteur est réparti vers les antennes ; c’est la raison pour laquelle on appelle ce dispositif un séparateur de puissance (Power Splitter).
Tout un article a été rédigé à ce sujet par ON1KSX (devenu ON8PS) dans le CQ-QSO, la revue des radioamateurs de l’UBA (Union Belge des Amateurs radio-émetteurs) en Belgique au milieu des années ’90.
Dans le cas de deux antennes 50 Ω mises ainsi en parallèle l’impédance au point de jonction est de 50/2 = 25 Ω. Pour adapter l’ensemble à une ligne de transmission de 50 Ω, un transformateur quart d’onde devrait avoir une impédance de :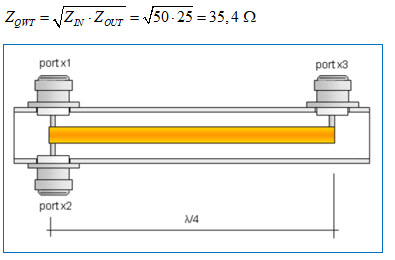

Fig. 92 : Diviseur de puissance (Power Splitter) adoptant le principe du transformateur quart d’onde pour raccorder deux antennes identiques sur le même Feeder. Source Hartmut Klüver DG7YBN, Allemagne.

Dans le cas de quatre antennes de 50 Ω en parallèle, l’impédance de l’ensemble est de 50/4 = 12,5 Ω et l’impédance du transformateur quart d’onde pour adapter l’ensemble à une ligne de 50 Ω devrait être de :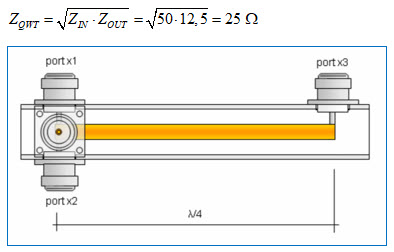

Fig. 93 : Idem ci-dessus, mais pour le raccordement de quatre antennes. Source Hartmut Klüver DG7YBN, Allemagne.

Comment fabriquer soi-même un transformateur quart d’onde d’une impédance caractéristique exotique ?

Le plus simple est de choisir un profilé (tube) de section carrée en aluminium ou en laiton d’une dimension standard et dont la dimension du côté de la section est suffisamment large pour permettre d’y apposer un connecteur type N ou UHF SO-239 à bride carrée. Ensuite il s’agit de trouver un tube en cuivre ou barreau en laiton d’un diamètre approprié pour obtenir une impédance caractéristique voulue pour le transformateur quart d’onde.

L’impédance caractéristique d’une ligne coaxiale est fonction du rapport du diamètre intérieur D de son enveloppe métallique extérieure (tresse, feuillard, tube annelé formable ou tube rigide) et du diamètre extérieur d du conducteur central.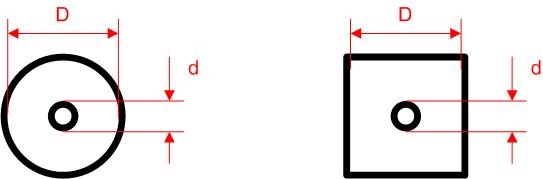

Fig. 94 : Ligne coaxiale dont le conducteur extérieur peut être de section circulaire ou carrée. Graphisme : ON4IJ.

Dans la pratique et le monde réel, le facteur de vélocité d’une ligne coaxiale dont l’isolant est de l’air sec est compris entre 0,95 et 0,99.

Fig. 95 : Diviseur de puissance (Power Splitter) en transformateur quart d’onde ici sous test avec quatre charges étalons et un mini analyseur de réseau vectoriel pour la mesure du SWR dans le domaine de la fréquence. Source Hartmut Klüver DG7YBN, Allemagne.
En ce qui concerne le transformateur quart d’onde, il y a lieu de bien se rappeler qu’il doit être prévu pour une fréquence bien précise. On peut toutefois constater que l’aspect sélectif d’un transformateur quart d’onde est fonction du rapport entre l’impédance d’entrée et de sortie qui doivent être adaptées. On peut visualiser cet effet par le relevé le la courbe du coefficient de réflexion dans le domaine de la fréquence.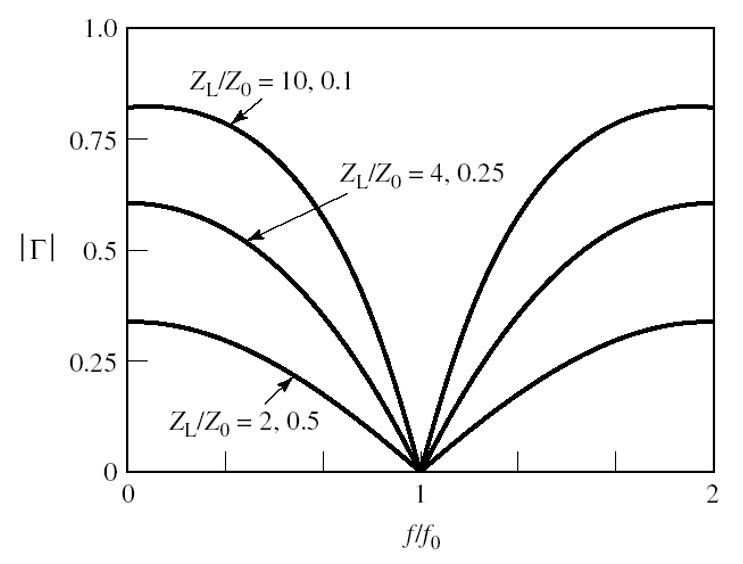

Fig. 96 : Coefficient de réflexion dans le domaine de la fréquence pour un transformateur quart d’onde en fonction du rapport entre l’impédance d’entrée et de sortie à adapter (Z_L/Z₀). Source Jim Stiles, University of Kansas, USA, EECS department (Electrical Engineering and Computer Science).
Toutefois, il y a moyen de construire un transformateur quart d’onde d’une certaine largeur de bande en plaçant plusieurs transformateurs quart d’onde les uns à la suite des autres en série en choisissant des impédances intermédiaires appropriées. Nous pouvons citer les transformateur quart d’onde à sections multiples suivant une progression binomiale et ceux qui suivent une progression selon les polynômes de « Chebyshev ». Les radioamateurs utilisent en général des transformateurs quarts d’onde à une ou deux sections en lignes coaxiales.
Les transformateurs quarts d’onde à sections multiples sont en général constitués de lignes de transmission fabriquées sur circuit imprimé en technique de micro ruban (Micro-Strip).

Voici une méthode de calcul pour un transformateur quart d’onde à sections multiples dont les impédances intermédiaires suivent une progression géométrique pas par pas. Chaque pas (Step) est un saut d’impédance d’une section à l’autre qui est défini comme suit :

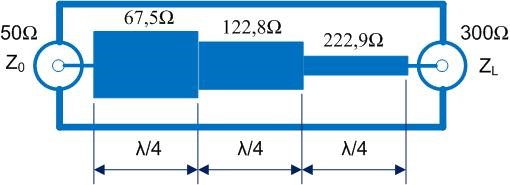
Fig. 97 : Transformateur quart d’onde à trois sections dont le calcul a été effectué à la page précédente. Graphisme : ON4IJ.

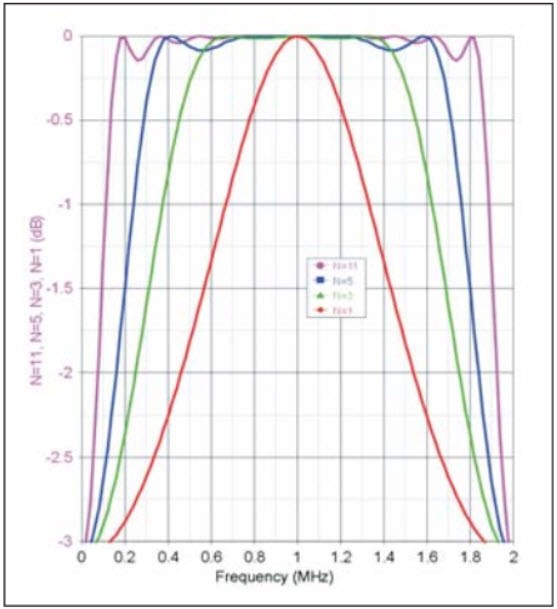
Fig. 98 : Bande passante de différents transformateurs quart d’onde à sections multiples. Orange : simple section ; Vert : trois sections ; Bleu : cinq sections ; Violet : onze sections. Source Agilent Keysight EEsof EDA (Electronic Engineering Software Electronic Design Automation), Matching Network Yin-Yang Part 2, April 2006, USA.

Adaptation avec deux transformateurs douzièmes d’onde raccourcis :

Un moyen très utile d’adapter une charge à une source est d’utiliser deux segments de ligne mis bout-à-bout et dont la longueur de chaque segment est proche de λ/12.
Cette méthode a été décrite dans le magazine QST Volume 81, N°6 de Juin 1997 pp 43-44 publié par l’ARRL. La découverte de ce système d’adaptation a été publiée par P. Bramham au CERN à Genève en novembre 1959.

Le premier segment de ligne d’une impédance caractéristique égale à celle de la source est placé du côté de la charge et le deuxième segment de ligne d’une impédance caractéristique égale à celle de la charge est placé du côté de la source ; voir figure ci-dessous. L’avantage de cet adaptateur est de pouvoir disposer de lignes de transmissions commerciales dont les impédances caractéristiques respectives sont celles de la source et de la charge. La somme des longueurs des deux segments est inférieure à celle d’un transformateur quart d’onde.

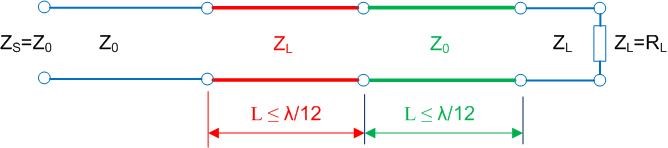
Fig. 99 : Adaptation avec deux transformateurs douzièmes d’onde raccourcis. Graphisme : ON4IJ.

Le calcul exact de la longueur de chaque segment s’effectue comme suit :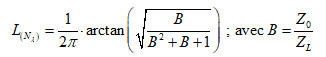

Exemple pratique :

On veut adapter une antenne d’impédance de 75 Ω à une ligne de transmission coaxiale en RG213U de 50 Ω. La fréquence de travail est de 50 MHz. On dispose de câble RG11U de 75 Ω. Le facteur de vélocité de ces deux types de câble est de 0,66. Quelle sera la longueur de chaque segment de ligne ?

L’adaptation par double transformateur λ/12 s’effectue pour une fréquence de travail bien précise comme c’est le cas pour un transformateur quart d’onde. On peut toutefois constater que l’aspect sélectif est fonction du rapport entre l’impédance d’entrée et de sortie qui doivent être adaptées. On peut visualiser cet effet par le relevé de la courbe du coefficient de réflexion dans le domaine de la fréquence.

Fig. 100 : Coefficient de réflexion dans le domaine de la fréquence pour un double transformateur douzième d’onde en fonction du rapport entre l’impédance d’entrée et de sortie à adapter (Z₀/Z_L). Source Darrel Emerson, Amsat AA7FV et G3SYS, Tucson Arizona USA, member of NRAO (National Radio Astronomy Observatory).
Pour les lecteurs passionnés sur le sujet des adaptations d’impédance, nous recommandons la série des dix articles rédigés par ON5WF dans le magazine CQ‑QSO de l’UBA entre Juin 2009 et Mars 2011. Ces articles sont disponibles sur le site Internet de l’UBA.

Logiciels informatiques sur l’abaque de Smith :

Il existe plusieurs logiciels disponibles pour résoudre des calculs de lignes de transmission et des réseaux d’adaptation d’impédance par différentes méthodes. Nous ne pouvons pas tous les présenter en revanche il existe un logiciel gratuit bien sympathique qui permet d’aborder de manière simple les applications de l’abaque de Smith : il s’agit du logiciel SimSmith réalisé par AE6TY.
Nous reprenons ci-dessous quelques applications numériques qui ont été décrites dans cet article et qui seront traitées par le logiciel SimSmith. Les tracés sont légèrement différents car il s’agit d’un abaque en impédance et en admittance (imittance). Les réactances suivent les cercles à résistance constante et les susceptances suivent les cercles à conductance constante.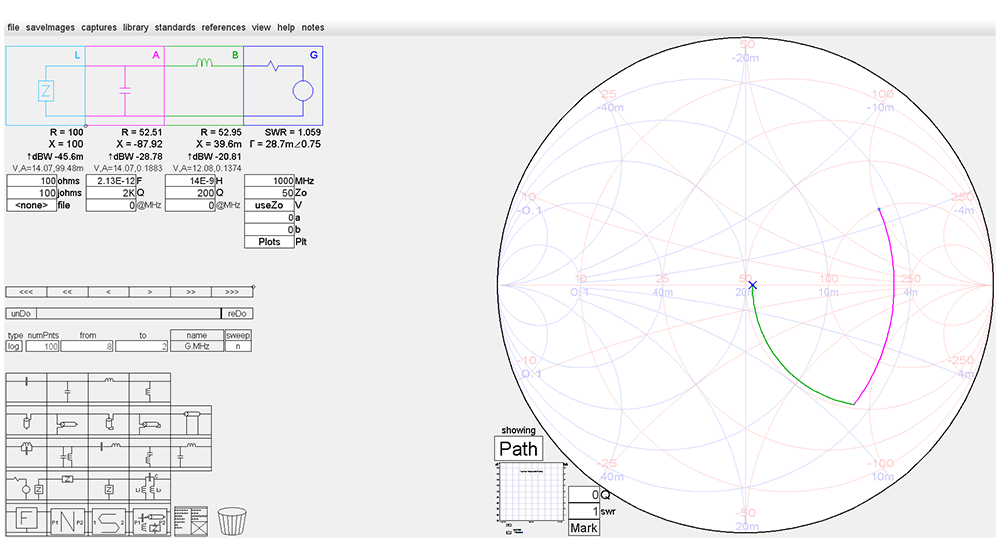

Fig. 101 : Adaptation d’une charge de 100+j100 Ω à 1 GHz à une source de 50+j0 Ω par un réseau adaptateur en « L » constitué d’un condensateur en parallèle de 2,13 pF sur la charge et d’une bobine d’induction de 14 nH en série avec la source. Voir figure 40 page 46. Source : SimSmith AE6TY.

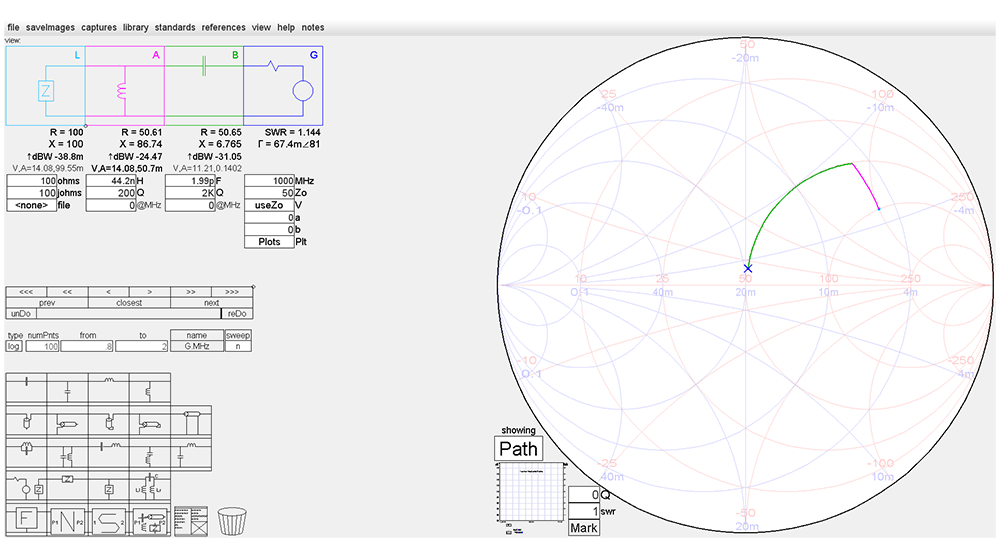
Fig. 102 : Adaptation d’une charge de 100+j100 Ω à 1 GHz à une source de 50+j0 Ω par un réseau adaptateur en « L » constitué d’une bobine d’induction en parallèle de 44,2 nH sur la charge et d’un condensateur de 1,99 pF en série avec la source. Voir figure 41 page 48. Source : SimSmith AE6TY.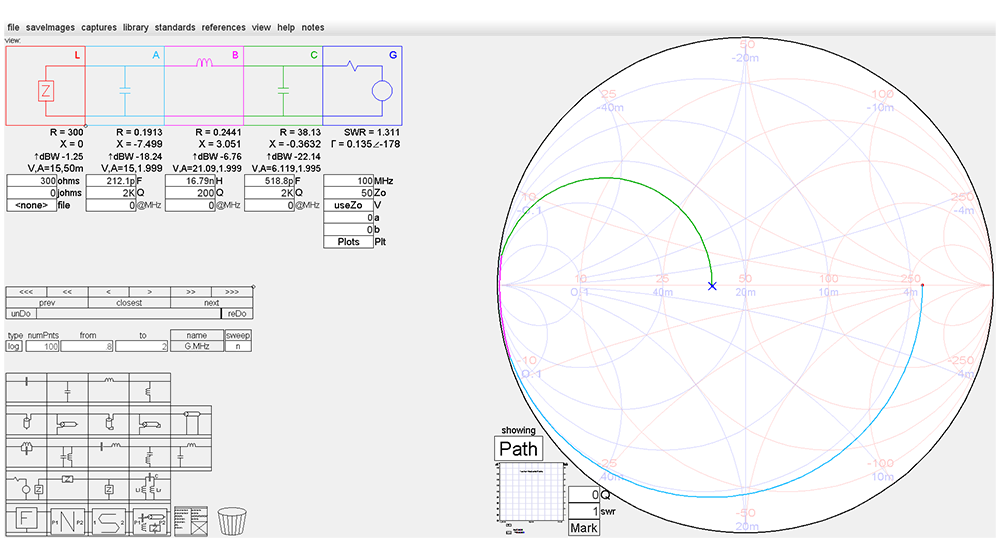

Fig. 103 : Tracé sur l’abaque de Smith d’un réseau en « PI » calculé pour une charge de 300 Ω et pour une source de 50 Ω sur une fréquence de travail de 100 MHz avec une bande passante de 5 %, c’est-à-dire de 5 MHz. Voir figure 50 page 59. Remarque : ici, l’adaptation est presque parfaite ; les composants doivent être légèrement ajustés. Le logiciel tient compte du facteur de qualité des composants pour se rapprocher de la réalité. Le Q d’une bobine d’induction étant au maximum de l’ordre de 200, c’est la valeur de l’inductance qui devrait ici être ajustée. Source : SimSmith AE6TY.

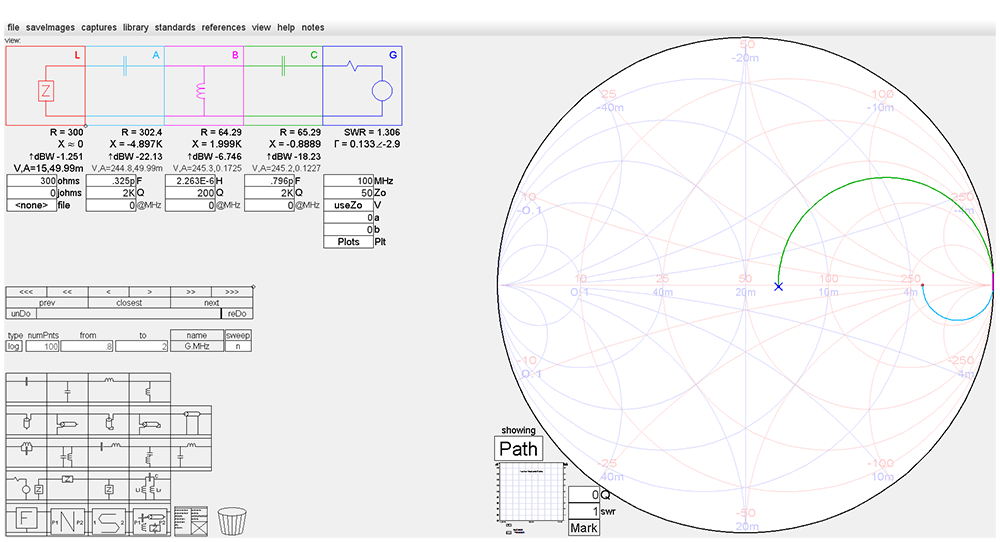
Fig. 104 : Tracé sur l’abaque de Smith d’un réseau en « TÉ » calculé pour une charge de 300 Ω et pour une source de 50 Ω sur une fréquence de travail de 100 MHz avec une bande passante de 5 %, c’est-à-dire de 5 MHz. Voir figure 54 page 65. Même remarque que celle de la figure précédente ci-dessus. Source : SimSmith AE6TY.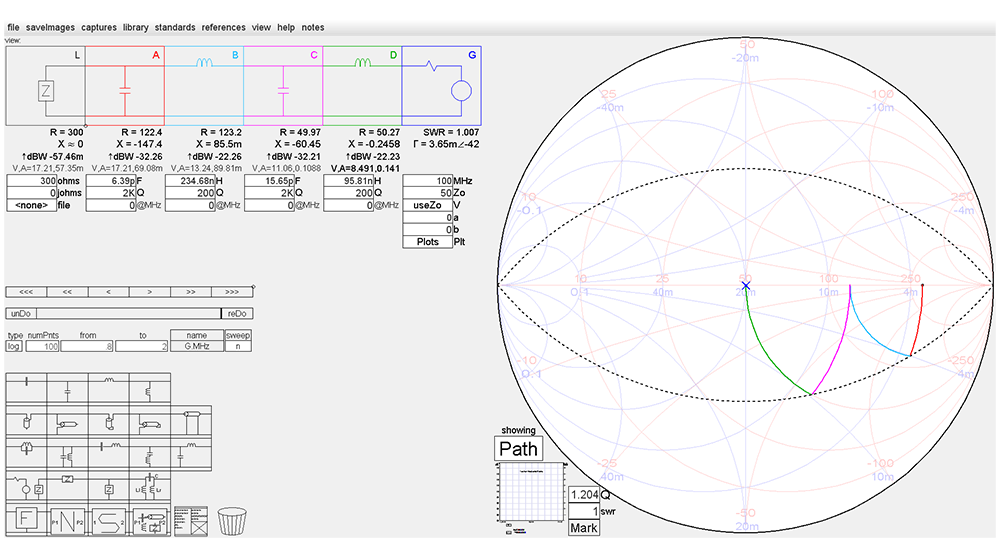

Fig. 105 : Tracé sur l’abaque de Smith d’un réseau en « double L » large bande calculé pour une charge de 300 Ω et pour une source de 50 Ω sur une fréquence de travail de 100 MHz avec un Q_n = 1,2. Voir figure 62 page 73. On observera l’optimalisation des réactances pour obtenir le facteur de qualité visé qui est bien visible sur le cercle à Q constant tracé sur l’abaque. Source : SimSmith AE6TY.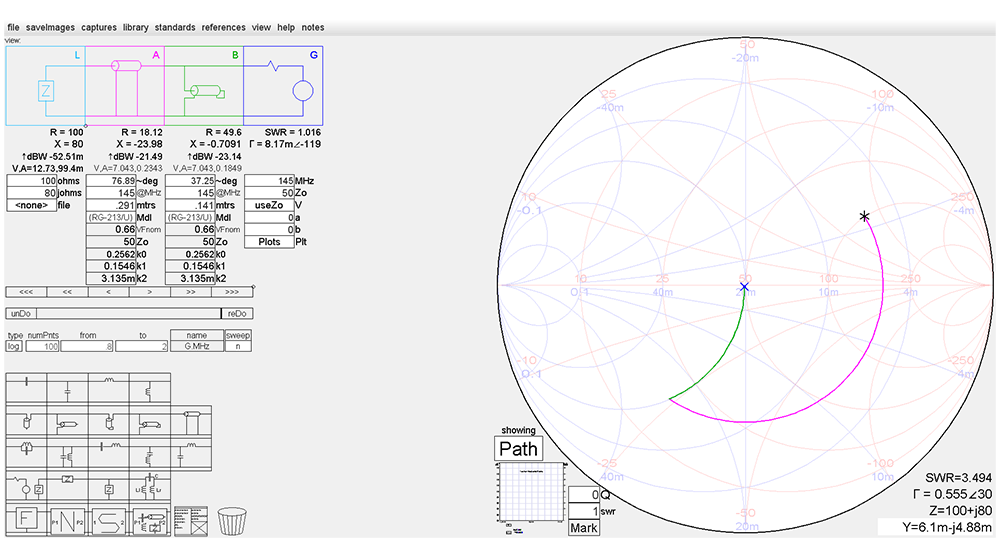

Fig. 106 : Calcul de la distance par rapport à la charge et de la longueur d’un Stub en parallèle sur une ligne de transmission RG213U pour adapter une antenne d’impédance complexe de 100+j80 Ω à une fréquence de travail de 145 MHz. Voir figure 79 page 95. Source : SimSmith AE6TY.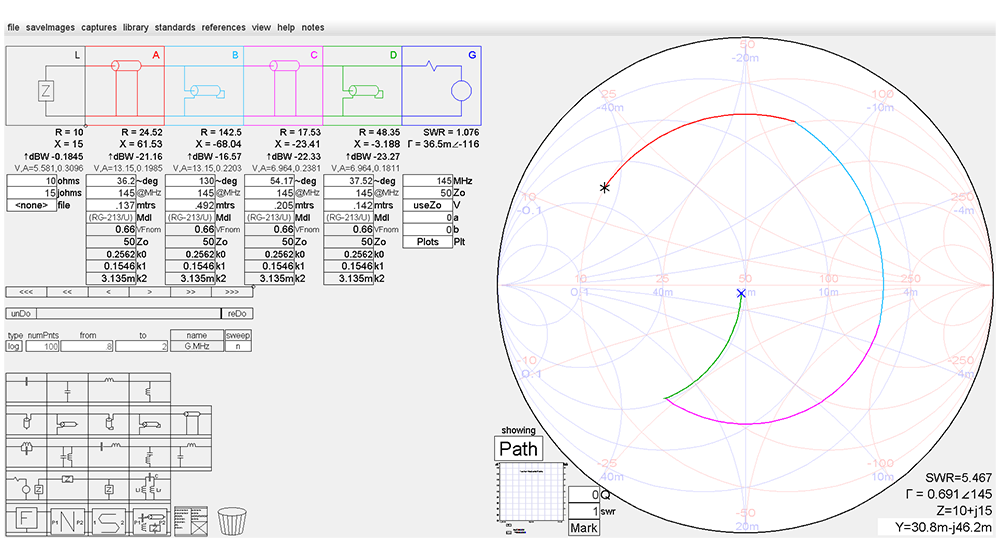

Fig. 107 : Adaptation par double Stub en court-circuit et en parallèle sur une ligne coaxiale en câble RG213U. L’impédance de la charge est de 10+j15 Ω à une fréquence de 145 MHz. Voir figures 80 à 84 des pages 97 à101. Source : SimSmith AE6TY.

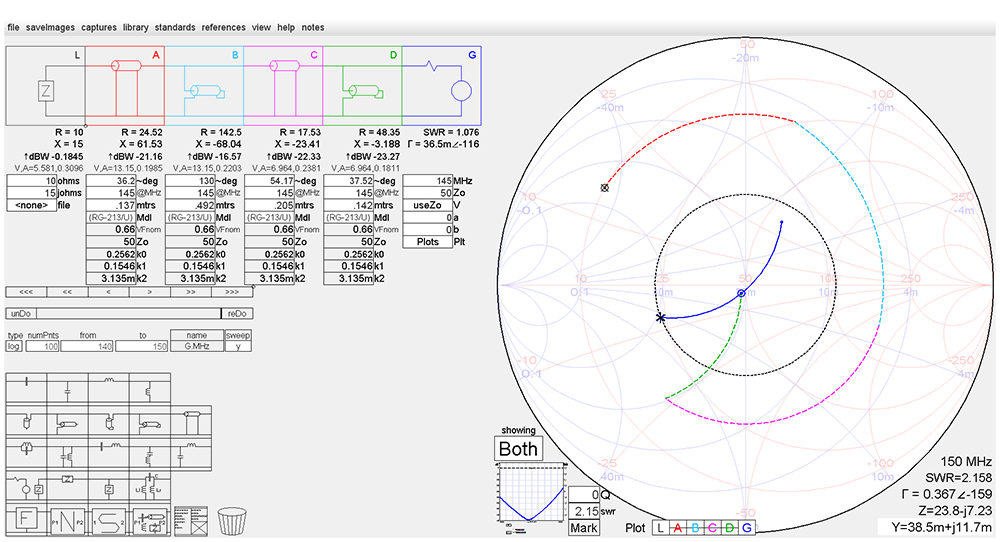
Fig. 108 : Idem ci-dessus avec balayage en fréquence entre 140 MHz et 150 MHz. On peut observer la courbe en bleu passant par le centre de l’abaque : il s’agit du lieu géométrique de l’impédance complexe vue par la source dans le domaine de la fréquence. Le rapport d’ondes stationnaires est de 2,15:1 à la fréquence de 150 MHz sur le cercle à SWR constant tracé sur l’abaque. La réponse du SWR dans le domaine de la fréquence est visible dans un encadré en bas à gauche de l’abaque. Source : SimSmith AE6TY.

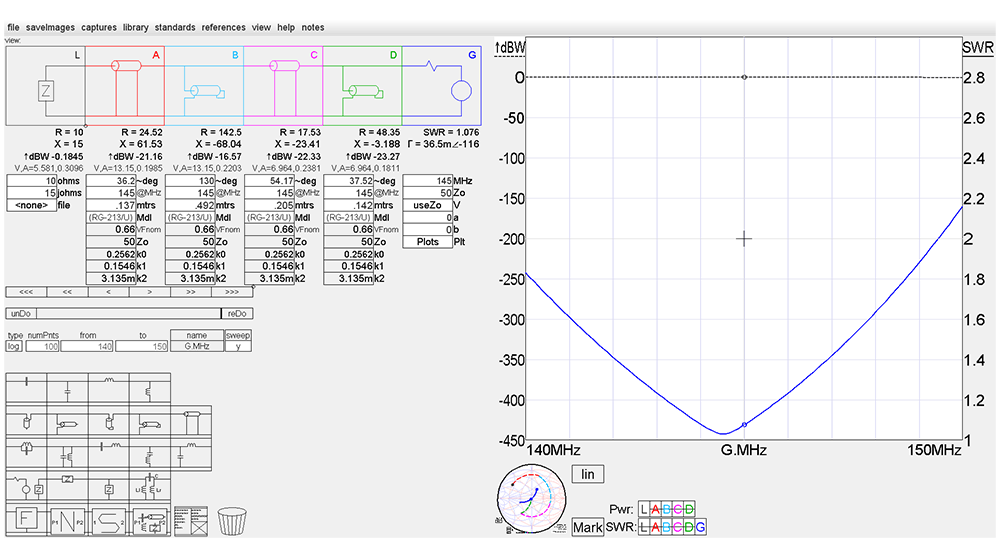
Fig. 109 : Idem ci-dessus avec balayage en fréquence entre 140 MHz et 150 MHz. Tracé du SWR dans le domaine de la fréquence. Le ROS est de 1,83:1 à 140 MHz ; 1,07:1 à 145 MHz et 2,15:1 à 150 MHz. L’abaque de Smith est visible dans l’encadré en bas à gauche du graphique. Source : SimSmith AE6TY.
Pour la suite, c’est à vous d’effectuer d’autres simulations en faisant varier tous les paramètres que vous voulez avec les curseurs du clavier de votre ordinateur afin d’observer les changements en temps réels sur l’abaque de Smith.

Conclusions

Bien comprendre l’abaque de Smith, c’est mieux maîtriser les phénomènes qui se produisent dans les lignes de transmission et bien anticiper les variations d’impédance dans le domaine de la fréquence. C’est aussi casser certains mythes au sujet du rapport d’ondes stationnaires.
Après avoir assimilé le contenu de cet article, vous serez fins prêts à aborder l’utilisation d’un analyseur de réseaux vectoriel pour la mesure du S₁₁ et du S₂₂ avec affichage de l’abaque de Smith à l’écran de l’appareil de mesure.

Deuxième partie de cet article, cliquer sur ce LIEN

Cet article peut être téléchargé au format PDF. Il suffit de cliquer sur ce lien :

Download (71)

A propos de l'auteur

Jean-François ON4IJ

Bonjour.
Je suis né en 1960 et père de deux enfants. J’ai obtenu ma licence HAREC en 1984 et j’ai repris l’indicatif de mon père, ON4IJ, en 2016. Je suis passionné par les instruments de mesure radiofréquence et j’ai créé un laboratoire pour expérimenter et améliorer mes connaissances en électronique HF. Je contribue au site Internet ON5VL.org en publiant des articles techniques sur mes expériences radioamateur. Ces articles sont illustrés et écrits de manière didactique, avec un ton pratique et ludique. Vous y trouverez des explications techniques et mathématiques, mais toujours dans le but de partager mes connaissances et d’aider les autres radioamateurs. 73 à tous. ON4IJ.

See author's posts