Même si elle attire très peu l’attention, hormis peut-être son prix, la ligne d’alimentation est un acteur important dans le fonctionnement de nos systèmes d’antennes. Bien la connaître nous est utile pour assurer et améliorer les performances de nos équipements de radioamateurs.

L’onde stationnaire, du courant et de la tension, Il n'est pas toujours facile d'expliquer un principe, même simple, comme la présence et la manière dont deux courants ou deux tensions qui se déplacent en sens contraire le long d’un conducteur peuvent donner naissance à une forme particulière du courant et de la tension le long du conducteur. Il ne s’agit pas ici d’une « interférence » de l’un envers l’autre, l’un perturbant le comportement de l’autre, car chacun agit suivant les critères qui lui sont propres. Il s’agit au contraire d’une superposition (en mathématiques, la somme vectorielle) sur la longueur du conducteur de deux composantes électriques de même nature, tension ou courant, se déplaçant en sens contraire le long du conducteur. Nous débutons par l’analyse d’une image connue de tous. Contenus de l'article

• 1. Faire des ronds dans l’eau.
  • 1.1 L’onde progressive
  • 1.2 L’onde progressive incidente
  • 1.3 L’onde progressive réfléchie
  • 1.4 L’onde stationnaire
• 2. Un conducteur de longueur finie ouvert à son extrémité
  • 2.1 Le rebond de la tension et du courant incident à la sortie du conducteur
  • 2.2 Impédance en un point du conducteur, soit le rapport entre l’onde stationnaire de tension à l’onde stationnaire de courant
• 3. La ligne d’alimentation
  • 3.1 Schéma électrique équivalent d’une ligne d’alimentation
  • 3.2 Impédance caractéristique de la ligne
  • 3.3 La ligne d’alimentation est adaptée à sa sortie
    • 3.3.1 L’adaptation d’impédance
  • 3.4 La ligne d’alimentation n’est pas adaptée à sa sortie
    • 3.4.1 La ligne d’alimentation est ouverte à sa sortie
    • 3.4.2 La ligne d’alimentation est en court-circuit à sa sortie
    • 3.4.3 La ligne d’alimentation est chargée par une impédance différente de son impédance caractéristique

• 4. Le R.O.S. et tout ça, tout ça

• 5. La ligne avec perte

1. Faire des ronds dans l’eau.

1.1 L’onde progressive

Elle peut être considérée comme l’ondulation provoquée en surface par une pierre qui tombe dans une eau stagnante. A la pénétration de la pierre dans l’eau il va se former une ondulation circulaire de l’eau qui va progresser dans toutes les directions avec comme centre le point de rencontre de la pierre avec l’eau. Cette ondulation qui se déplace, porte le nom d’onde progressive, car elle progresse, elle s’éloigne, de son origine, et chaque point de la surface de l’eau à n’importe quelle distance du centre voit passer, à un moment donné, le mouvement en amplitude de l’ondulation. Il est bien évident, que dans cet exemple précis, l’amplitude ira en diminuant en fonction de sa distance par rapport au centre. Ceci est dû à la force d’inertie de l’eau qui « atténue » l’amplitude de l’ondulation à mesure de sa progression. Cependant chaque point du cercle verra passer la même variation d’amplitude que tous les autres points de ce cercle. Expérience : si nous déposons une balle de ping-pong à la surface de l’eau à une petite distance du point de chute de la pierre, cette balle de ping-pong va s’éloigner progressivement de ce point en suivant l’ondulation dans sa progression.

1.2 L’onde progressive incidente

Nous reprenons l’exemple de l'eau mais cette fois contenue dans un bassin de forme cylindrique à bords verticaux, afin de limiter le trajet du déplacement de l’eau. Nous laissons tomber notre pierre au centre. La chute de la pierre provoque, comme dans l’exemple précédent, une ondulation circulaire qui progresse en un rayon de plus en plus grand vers le bord du bassin. C’est ce que nous appelons une onde progressive « incidente » au bord, l’extrémité du bassin. L’amplitude de l’ondulation va en diminuant à mesure qu’elle s’éloigne du point de chute, comme expliqué dans l’exemple précédent.

1.3 L’onde progressive réfléchie

Une fois le bord atteint, l’ondulation incidente, devrait normalement disparaître, « s’écraser » sur le bord et l’eau retrouver immédiatement sa planitude. Cependant nous pouvons observer à proximité du bord, un court instant après, une ondulation qui pourrait être interprétée comme une rémanence de l’ondulation incidente. Cependant comme nous le savons, ce comportement trouve son origine dans le reflux de l’eau provoqué par le bord du bassin. Expérience : si nous déposons notre balle de ping-pong à la surface de l’eau, à proximité du bord, la balle de ping-pong va se soulever une première fois avec l’ondulation incidente et une fraction de seconde après, une seconde fois. Ce qui nous donne l’image d’une balle immobile en déplacement (stationnaire) mais agitée verticalement à deux reprises. Ici, il est nécessaire de se rappeler la loi générale de la continuité de l’énergie qui nous enseigne qu’une énergie une fois produite ne disparaît simplement pas. Elle peut éventuellement se transformer en une autre énergie, comme l’énergie de mouvement contenue dans la circulation de l’eau d’une rivière qui fait tourner la roue à aubes d’un moulin, elle se transforme en une énergie mécanique de rotation de la pierre. Dans le cas présent, l’énergie de l’eau en mouvement vers le bord du bassin, l’ondulation incidente, va se transformer en une énergie de même nature et d’amplitude équivalente, une ondulation, cette fois en retour du mouvement initial de l’eau. C’est ce que nous appelons une onde progressive « réfléchie » par le bord du bassin. Nous avons observé à partir de ce moment, deux ondulations successives dans un déplacement en sens inverse sur la distance centre-bord. Ces deux ondes progressives, qui se succèdent dans le présent exemple, contiennent chacune une énergie de même nature.

1.4 L’onde stationnaire

Si maintenant, au lieu de laisser tomber une pierre dans l’eau, nous exerçons un mouvement périodique régulier de haut en bas (alternatif) à l’aide d’un bâton planté verticalement dans l’eau nous allons provoquer à sa surface une ondulation permanente, une ondulation progressive entretenue, sous la forme de cercles concentriques régulièrement espacés au rythme du mouvement du bâton. Ces ondulations progressives incidentes au bord vont successivement « s’écraser » sur le bord et produire chacune en retour, l’ondulation réfléchie que nous avons observée lors de l’expérience précédente. Cette fois cependant, chaque onde incidente vers le bord va être confrontée à chaque instant de son parcours, à la succession des ondes réfléchies générées par les ondes incidentes qui la précède. Ce que nous observons maintenant, est que les ondulations initiales, progressives incidentes, deviennent l’image d’une suite d’ondulations immobilisées, à des distances régulières du bord, mais toujours variables en amplitude. Cette «image » nous l’appelons « onde stationnaire ». L’onde stationnaire n’existe donc pas par elle-même car il faut à la fois une onde progressive incidente et une onde progressive réfléchie pour « former» l’onde stationnaire. Ce n’est donc pas une troisième ondulation, un troisième mouvement de l’eau, elle ne contient aucune énergie propriétaire. Seules existent les énergies contenues respectivement dans l’ondulation incidente et dans l’ondulation réfléchie. A chaque emplacement du parcours entre le centre et le bord, l’amplitude de l’ondulation stationnaire, cette « image » est formée par la superposition des amplitudes instantanées de l’ondulation incidente et réfléchie à cet emplacement. Expérience : Si en conservant le mouvement du bâton, nous déposons à la surface de l’eau, une balle de ping-pong, en n’importe quel endroit entre le centre et le bord, notre balle subira toujours un mouvement de bas en haut, mais restera « stationnaire » à l’endroit où elle à été déposée.

En résumé : L’ « onde stationnaire », (l’ondulation stationnaire) est le résultat du « déplacement ondulatoire »  (le courant) de l’eau, dans un sens, du centre vers le bord, que nous appelons « onde progressive incidente », (ondulation incidente) et dans le sens inverse, du bord vers le centre, que nous appelons « onde progressive réfléchie » (ondulation réfléchie). Une onde stationnaire ne peut exister que par la présence simultanée de deux ondes progressives se déplaçant en sens contraire.

2. Un conducteur de longueur finie ouvert à son extrémité

Comment se forme l’onde stationnaire le long d’un conducteur de longueur finie ? L’analyse précédente n’est rien d’autre que « l’image » qui est formée lorsqu’une tension alternative (un champ électrique) est appliquée à l’entrée d’un conducteur dont la sortie, est ouverte, non connectée à une charge dissipative. Nous pouvons assimiler le mouvement alternatif (de haut en bas) du bâton dans l’eau à un générateur de tension alternative et le déplacement ondulatoire de l’eau (le courant d’eau), à la progression de la tension, et du courant électrique qui l’accompagne, le long du conducteur au départ de la source de tension, son entrée, en direction de son extrémité ouverte, sa sortie.

2.1 Le rebond de la tension et du courant incident à la sortie du conducteur

Le courant progressif en provenance de l’entrée, le courant incident, se trouve brutalement arrêté dans sa progression à la sortie du conducteur, ce qui va provoquer deux phénomènes : 1) La loi de Lenz nous indique que cette variation brutale du courant va engendrer à cette extrémité une force contre-électromotrice alternative induite, un générateur de tension dont l’amplitude est proportionnelle à la vitesse de variation du courant  dans laquelle E est la force électromotrice induite et di/dt représente la vitesse de variation du courant i à cet endroit. (ici de x ampères à 0 ampère). La polarité de cette FEM alternative est en phase avec la tension incidente. Et donc à la sortie du conducteur nous aurons une tension dont l’amplitude est la somme de l’amplitude de la tension incidente et de l’amplitude de la F.E.M induite à cette extrémité. Cette tension induite va progresser en retour vers l’entrée et constituer l’onde progressive de « tension réfléchie ».   2) toujours en ce qui concerne l’arrêt brutal du courant incident, l’annulation de celui-ci à la sortie peut être comprise [*] comme le résultat de l’action d’un courant issu de cette extrémité, de même amplitude mais de phase opposée au courant incident. Ces deux courants se soustrayant l’un de l’autre à cet endroit donne un courant nul à la sortie du conducteur. Ce courant alternatif originaire (induit) par la sortie va progresser en retour vers l’entrée et constituer l’onde progressive de « courant réfléchi ». 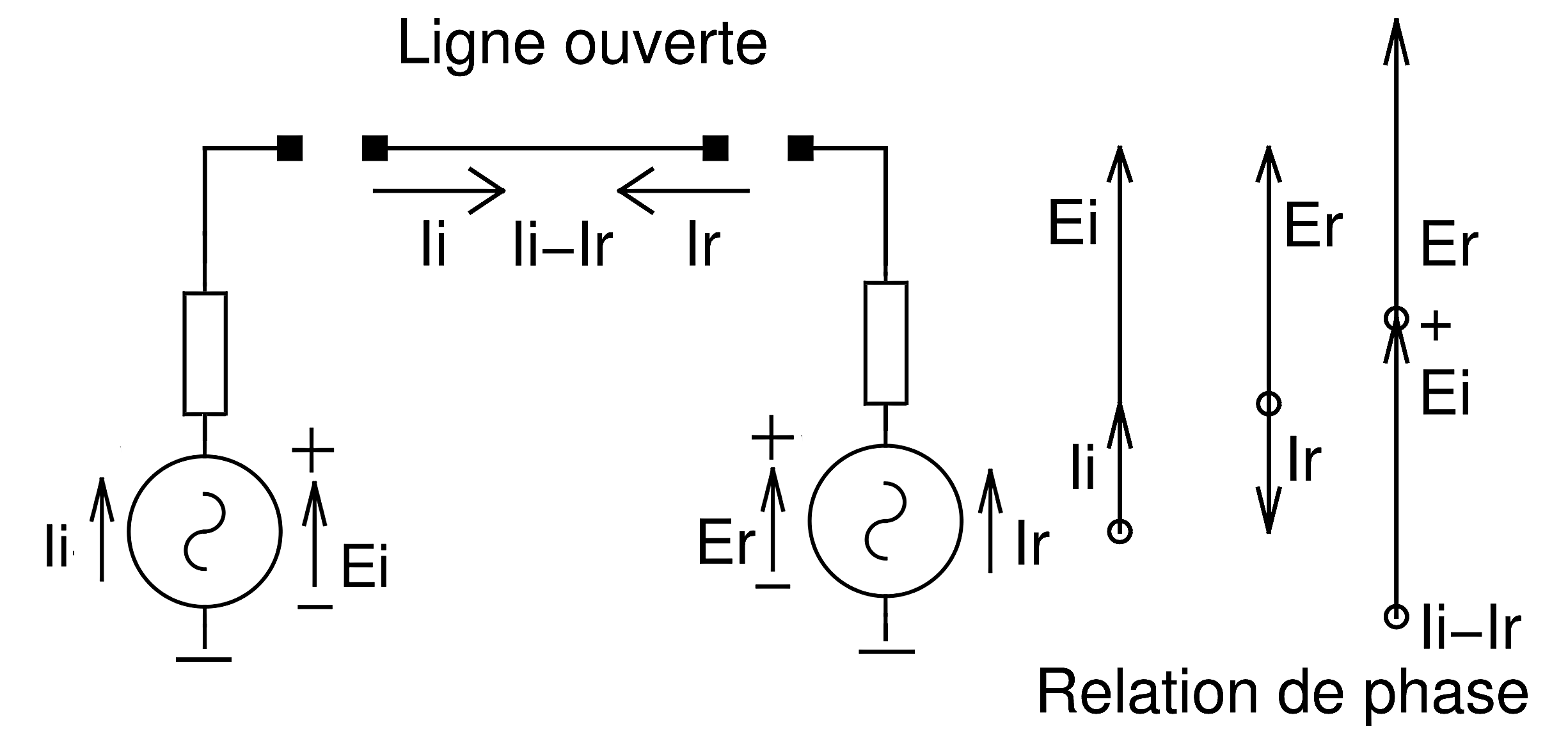De ce qui précède, nous pouvons schématiser la sortie comme un générateur de puissance réfléchie P_ref = V_ref  x  I_ref dont la tension V_ref est de même amplitude et phase avec la tension incidente V_inc et dont le courant Iref est de même amplitude mais en opposition de phase (180°) avec le courant incident I_inc. [*] Plus exactement, une tension génère un champ électrique et la propagation de ce champs électrique le long du conducteur va provoquer la circulation d’électrons libres dans le conducteur. Cette circulation d’électrons va engendrer un champ magnétique qui entoure le conducteur. L’énergie électrique est contenue dans ces deux champs. C’est le vecteur de Poynting. Comme l’a démontré, James Clerck Maxwell, un champ électrique variable, génère un champ magnétique et réciproquement un champ magnétique variable génère un champ électrique. La loi de Lenz ne fait que traduire ce principe. La tension et le courant qui constituent les ondes progressives incidentes de tension et de courant, sont en phase l’une par rapport à l’autre, puisque le conducteur est censé être purement résistif. Le produit de ces deux valeurs quantifie la puissance incidente P_inc = V_inc x I_inc. Comme la tension réfléchie à la sortie est en phase avec la tension incidente, et le courant réfléchi à la sortie est en opposition de phase (180°) avec le courant incident, cela signifie que la puissance réfléchie P_ref = V_ref x I_ref  est une puissance réelle et donc nullement réactive. La superposition ou la composition en amplitude et en phase (somme vectorielle), en chaque point  du conducteur, de l’amplitude instantanée de la tension progressive incidente et réfléchie, donne sur la longueur du conducteur, l’amplitude et la phase de ce qui ressemble à une tension stationnaire, stationnaire en position, mais ondulatoire en amplitude. Il n’y a donc pas sur le conducteur la présence d’un quelconque générateur de tension stationnaire. 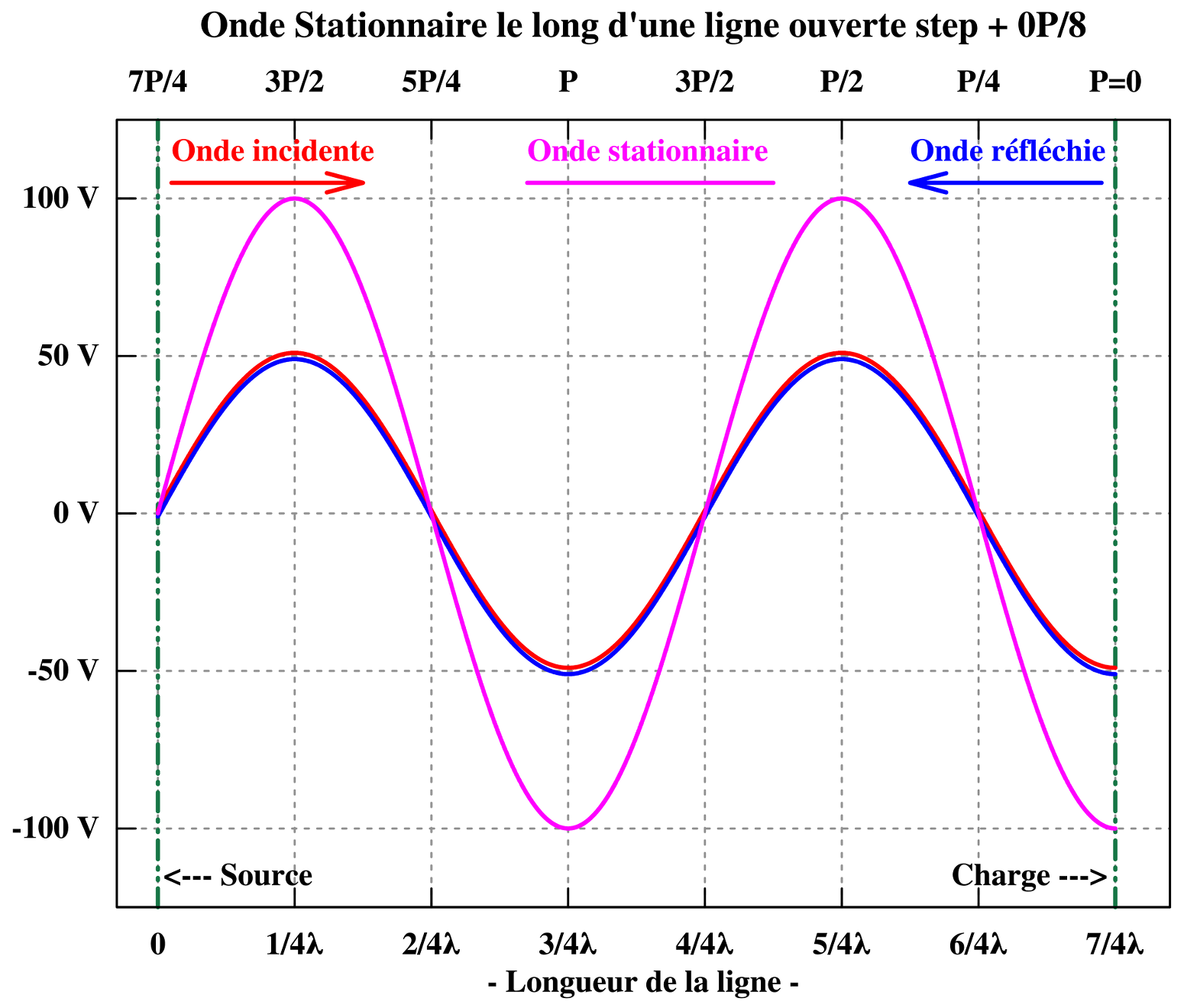Les 5 graphiques suivants reproduisent l’évolution de l’onde progressive incidente et réfléchie de tension, sur 1,3/4 de période par pas de 1/8 de période ainsi que la formation de l’onde stationnaire de tension correspondante.             De même, la superposition ou la composition en amplitude et en phase (somme vectorielle) en chaque point du conducteur de l’amplitude instantanée du courant progressif incident et réfléchi, donne sur la longueur du conducteur, l’amplitude et la phase de ce qui ressemble à un courant stationnaire, stationnaire en position, mais ondulatoire en amplitude. Il n’y a donc pas sur le conducteur la présence d’un quelconque générateur de courant stationnaire. 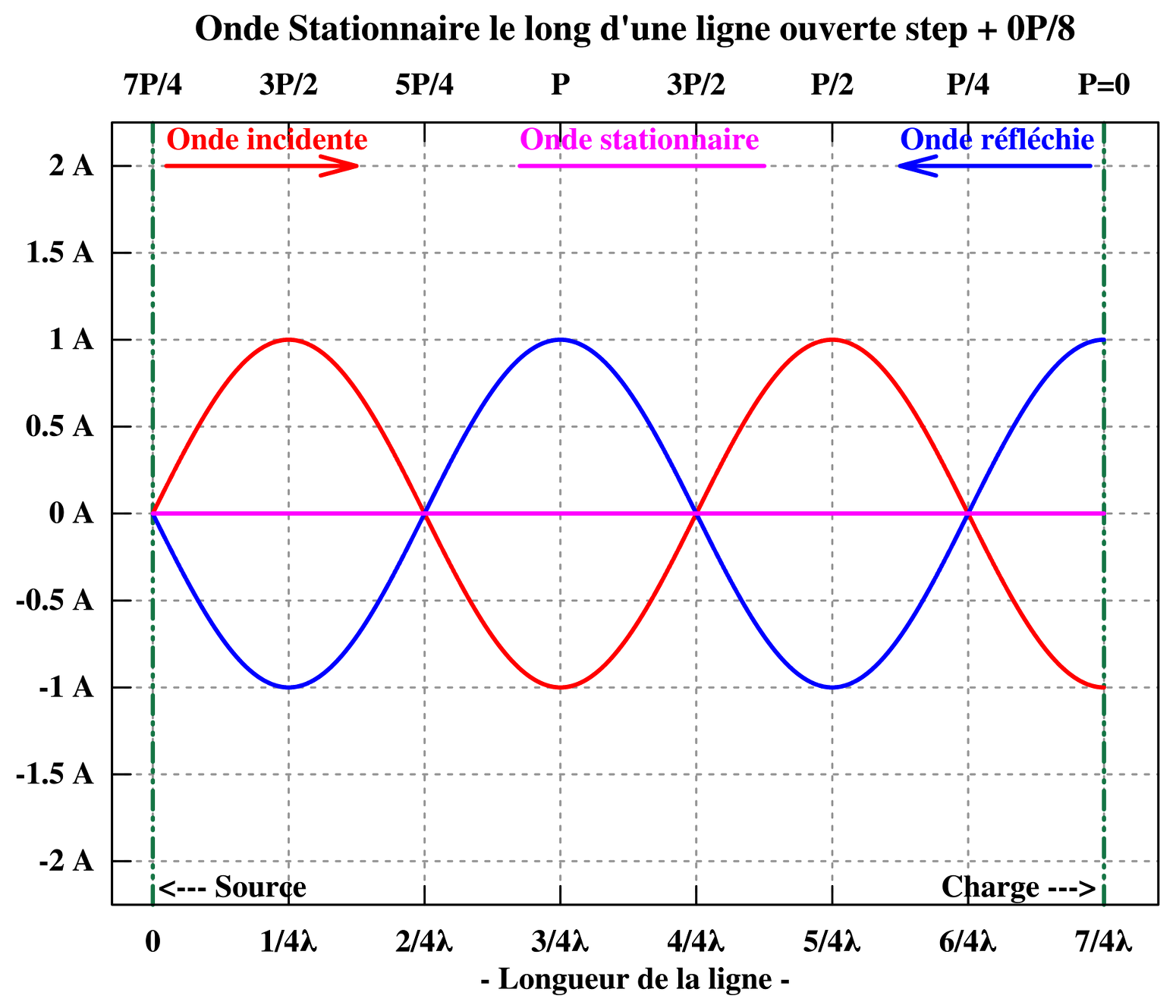Les 5 graphiques suivants reproduisent la progression de l’onde progressive incidente et réfléchie de courant, sur une 1,3/4 de période par pas de 1/8 de période ainsi que la formation de l’onde stationnaire de courant correspondante.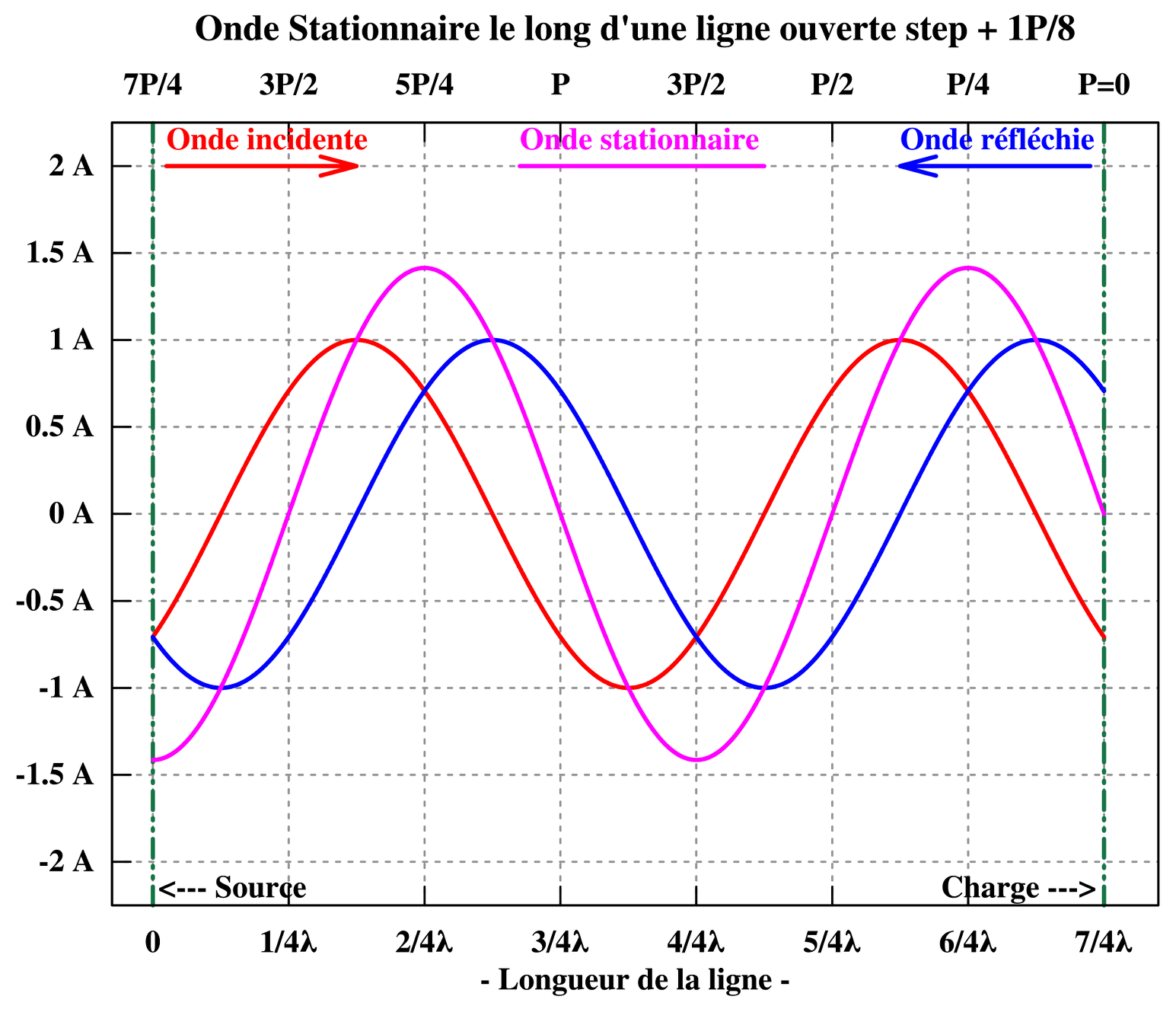    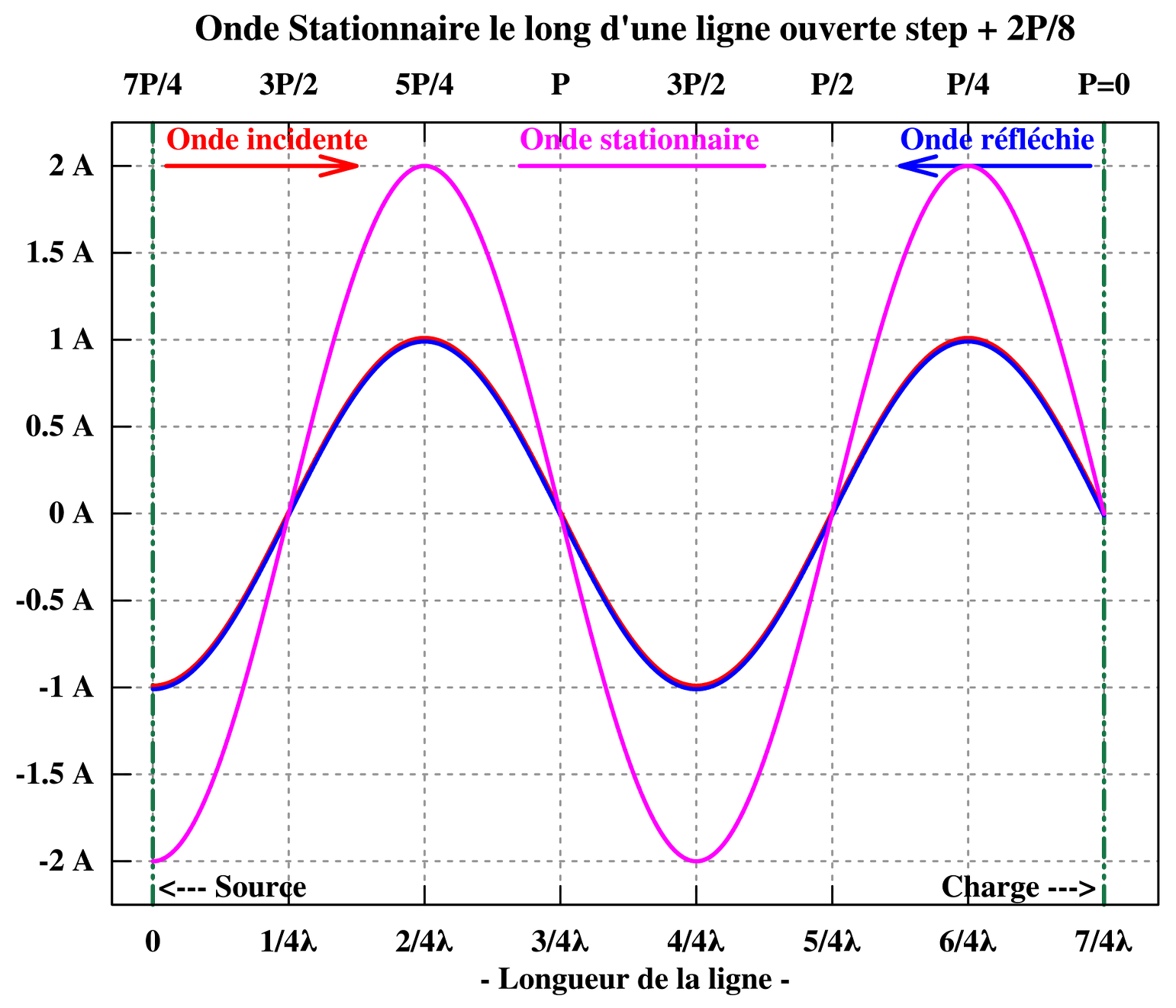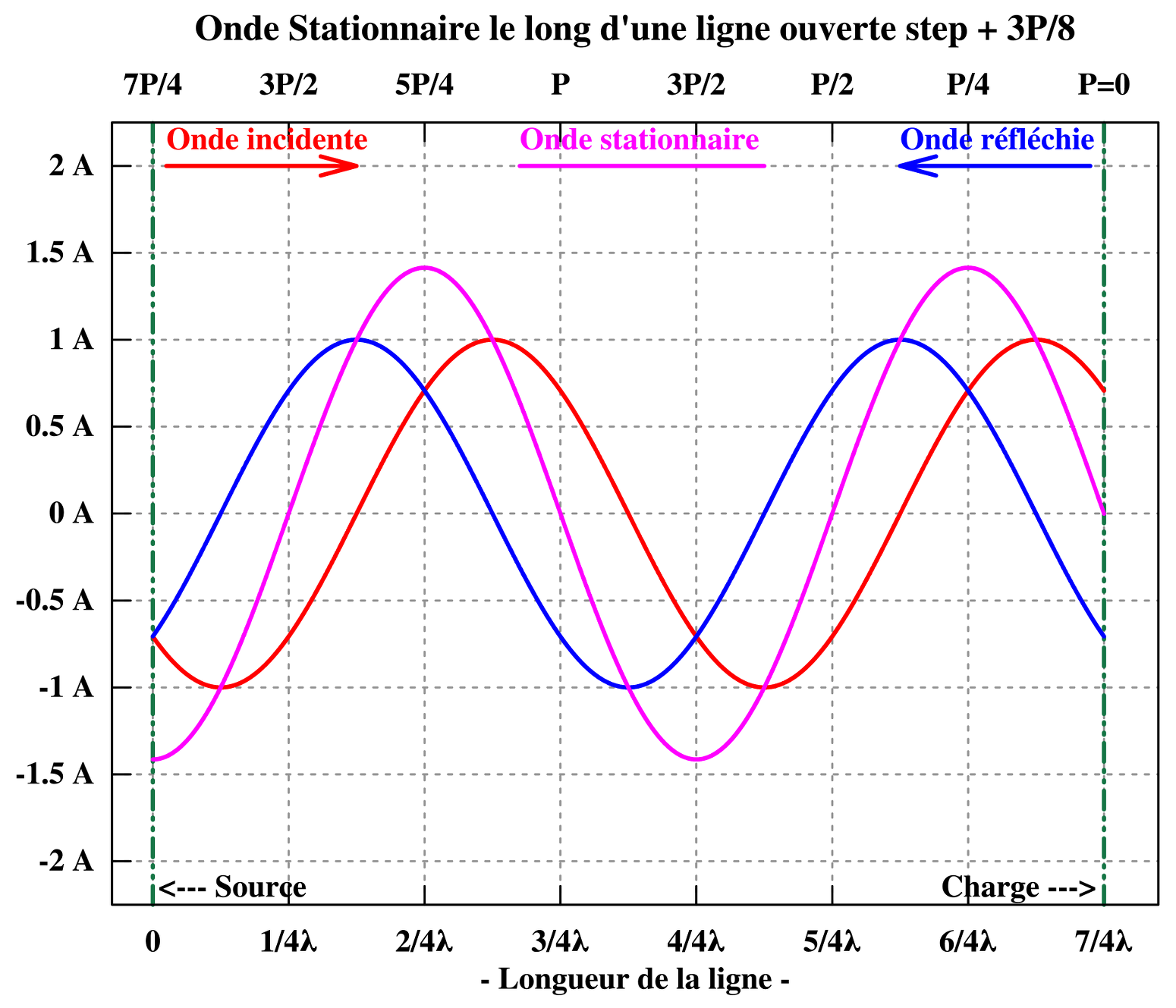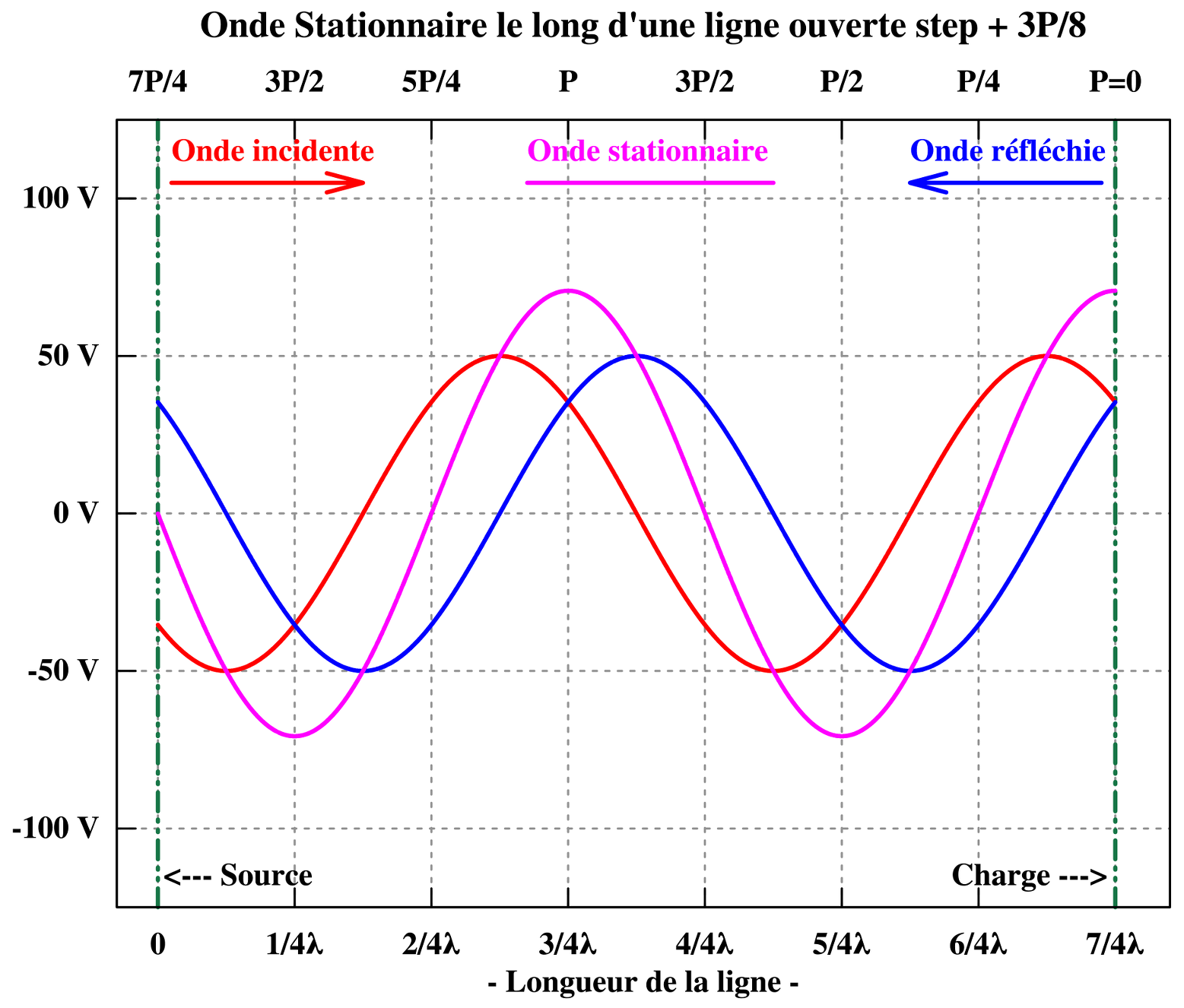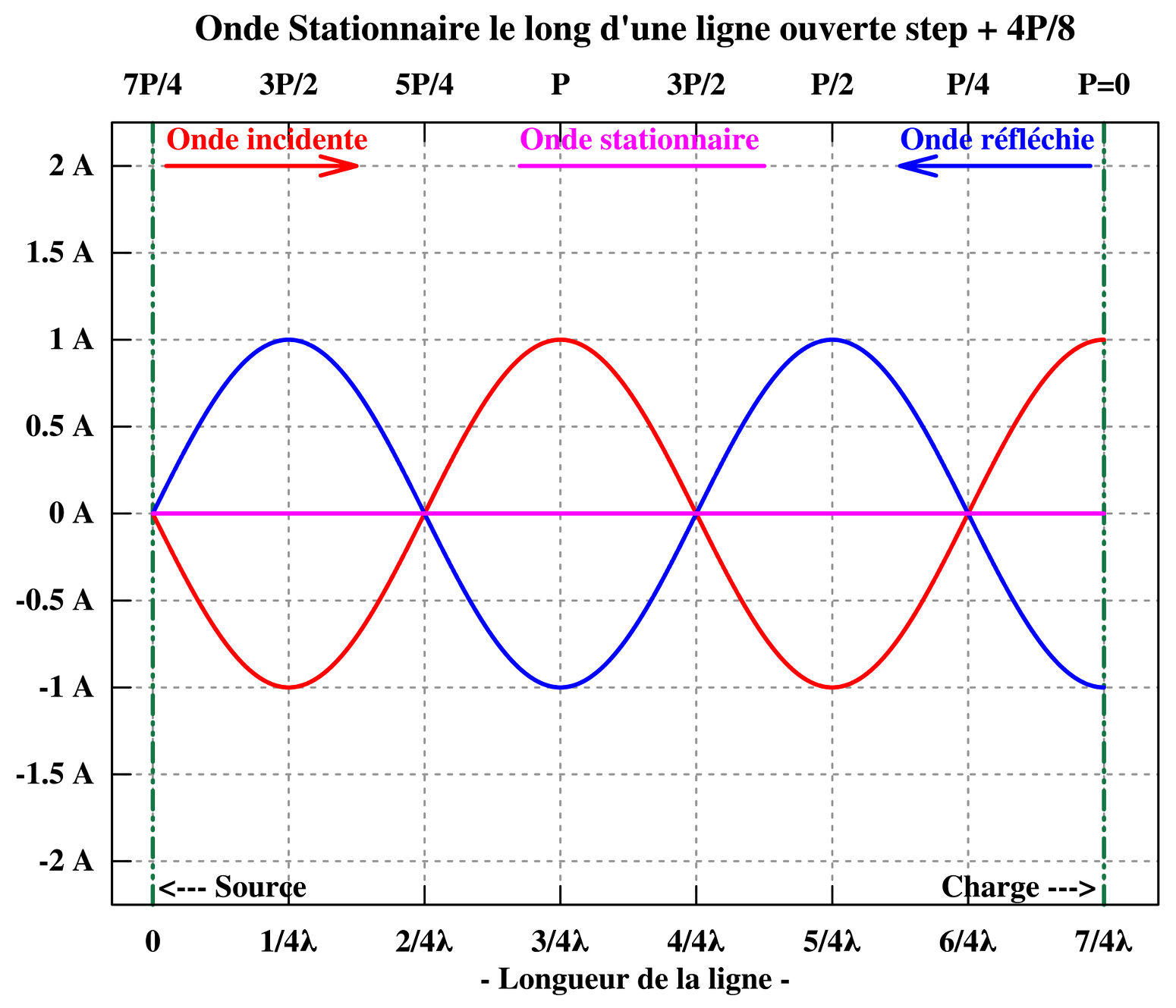         L’onde stationnaire de tension et de courant fait apparaître une répartition inégale, de l’amplitude de la tension comme celle du courant, le long du conducteur, contrairement à l’uniformité de l’amplitude de la tension et du courant progressif tout le long du conducteur. Lors de leurs progressions en sens contraire, la phase relative entre les deux tensions progressives évolue continuellement depuis la sortie : en phase, en retard de phase, en opposition de phase, en avance de phase et retour à en phase. Ce qui explique qu’en chaque point du conducteur l’amplitude réelle présente est la somme de deux amplitudes qui chacune est fonction de sa phase en ce point. L’amplitude de l’onde stationnaire de tension « ondule » ainsi entre un maximum, lorsque les deux tensions sont en phase, et un minimum, lorsque les deux tensions sont en opposition de phase. Le mécanisme est le même pour l’onde stationnaire de courant. Les graphiques ci-dessous représentent la variation d’amplitude sur plusieurs cycles complets de l’onde stationnaire de tension et de l’onde stationnaire de courant.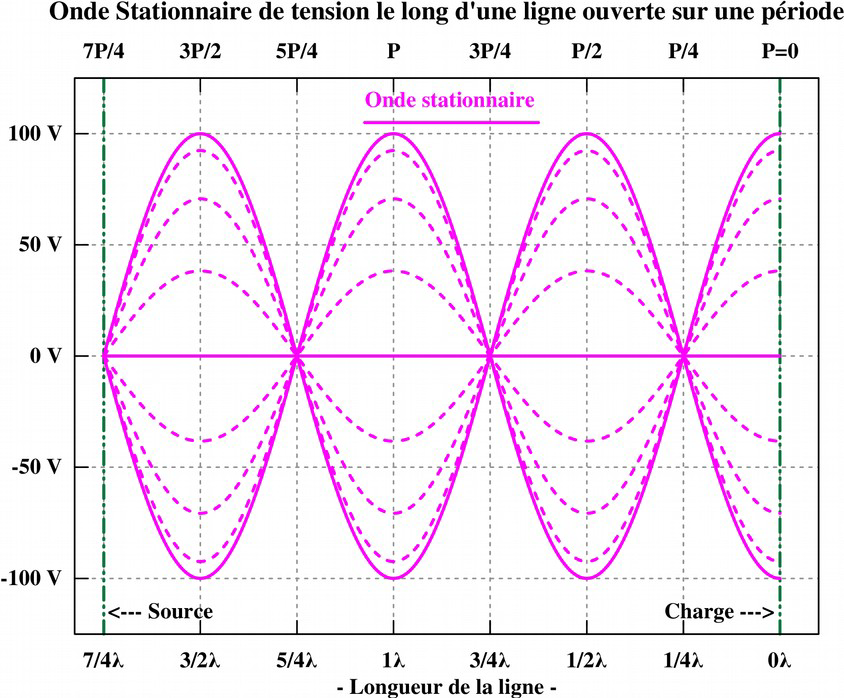 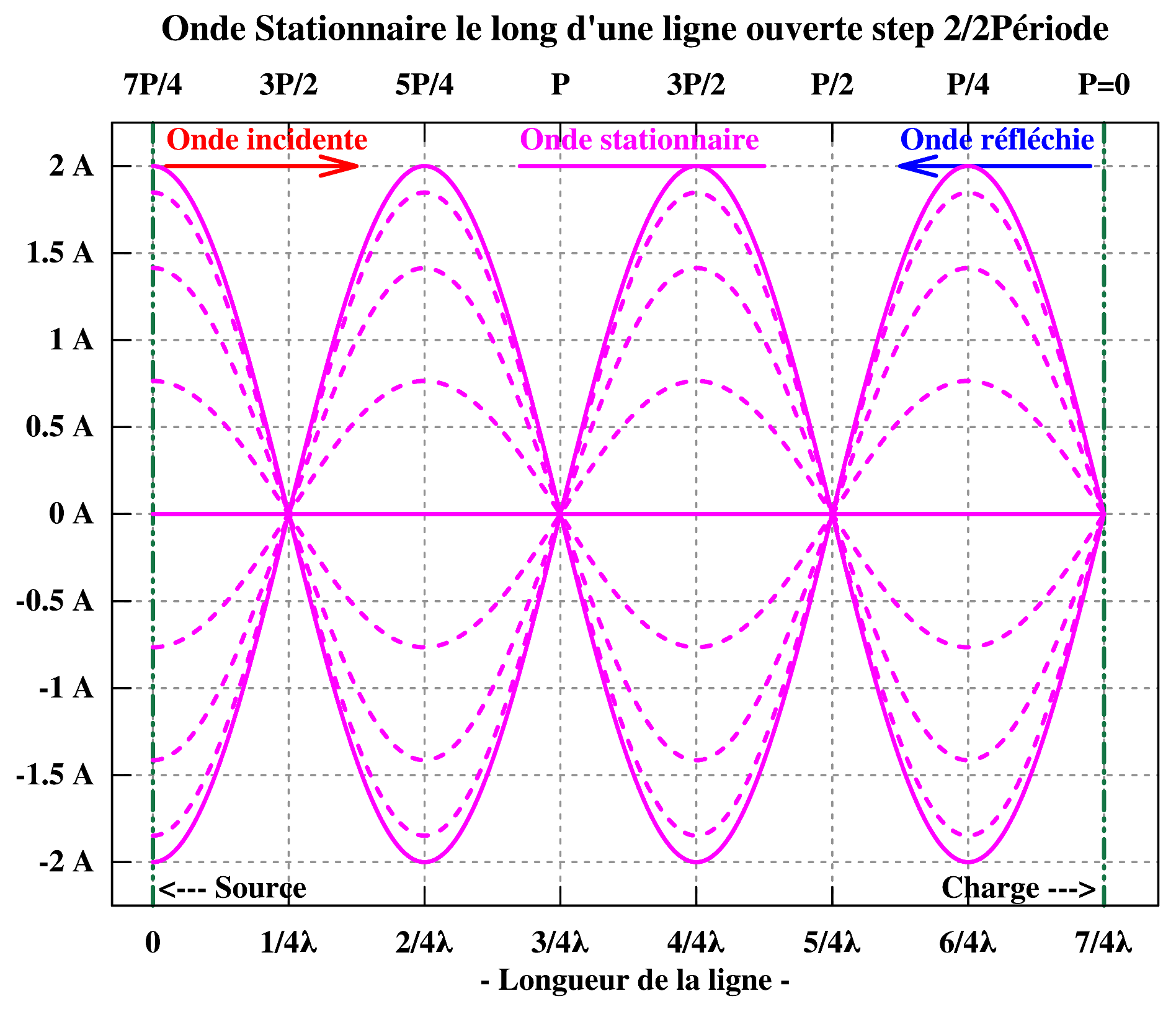L’onde stationnaire fait apparaître des « densités » de tension et de courant différentes en fonction de l’endroit où l’on se situe le long du conducteur. Celles-ci peuvent être « révélées » facilement en déplaçant le long du conducteur une petite boucle de cuivre isolé munie d’un détecteur ou simplement d’une petite ampoule (boucle de Hertz) pour situer les ventres (max) de courant, ou d’une ampoule néon pour situer les ventres (max) de tension. C’est l’un des principaux enseignements que nous offre l’onde stationnaire. Application L’application pratique de ce l’on vient d’analyser se trouve au niveau de l’antenne, où l’élément alimenté ayant une longueur finie (ouvert à sa sortie) sera le siège d’une onde stationnaire de tension et d’une onde stationnaire de courant, mais pratiquement c’est toujours la tension progressive incidente et réfléchie, ainsi que le courant progressif incident et réfléchi qui constituent les seuls porteurs d’énergie. Par contre la localisation de la haute densité de courant, donnée par l’onde stationnaire, nous indique particulièrement où sur l’antenne se situe le champ magnétique maximum et de rayonnement électromagnétique maximum.

2.2 Impédance en un point du conducteur, soit le rapport entre l’onde stationnaire de tension à l’onde stationnaire de courant

L’impédance en un point du conducteur est le second enseignement que nous procure l’onde stationnaire. Nous pouvons constater sur les diagrammes ci-dessous que l’onde stationnaire de tension et l’onde stationnaire de courant sont déphasées de 90° ou d’un quart de longueur d’onde tout au long du conducteur. Quand l’onde stationnaire de tension est maximum, l’onde stationnaire de courant est minimum et vice versa. Entre ces deux positions particulières nous voyons que l’onde stationnaire de courant, est soit en avance de phase, soit en retard de phase sur l’onde stationnaire de tension. Ce qui signifie qu’en un point quelconque de la longueur du conducteur, l’impédance, soit le rapport tension/courant des deux ondes stationnaires, va quantifier l’impédance et sa nature résistive, inductive ou capacitive. 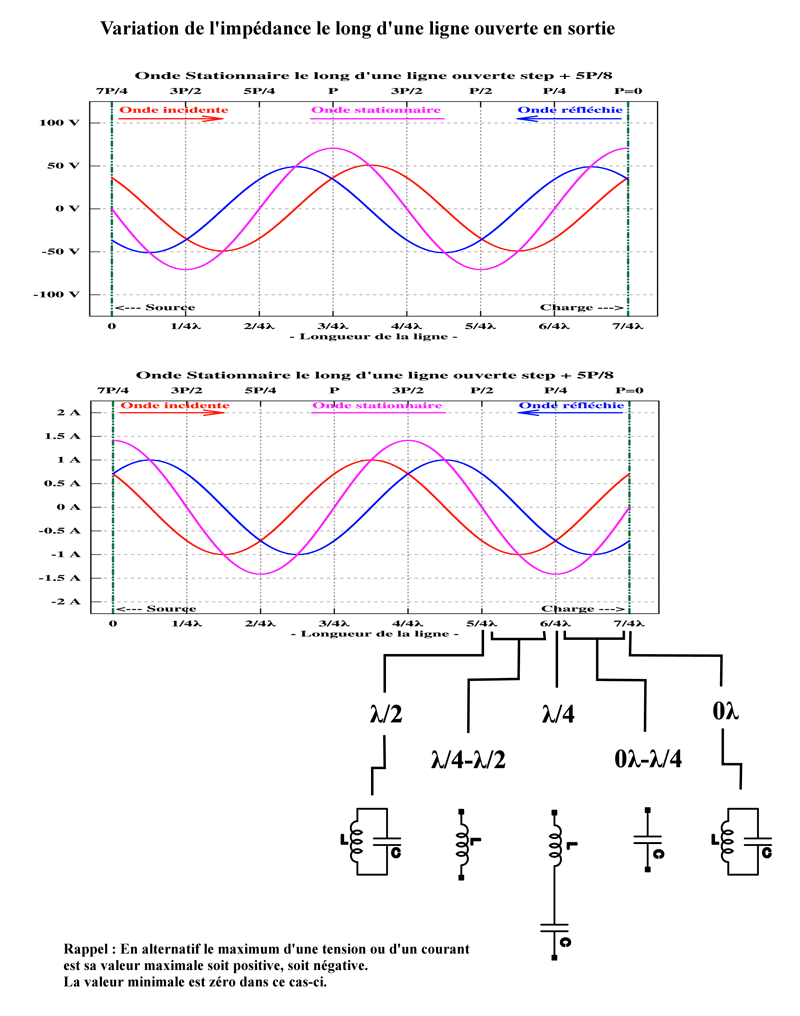Nous pouvons observer sur le graphique que la nature purement résistive de l’impédance se situe très précisément tous les quarts de longueur d’onde à compter de la sortie ouverte, alternativement une résistance élevée (équivalent à un circuit résonnant parallèle), suivi à un quart d’onde plus en retrait de la sortie, d’une faible résistance (équivalent à un circuit résonnant série), et ainsi de suite. A tous les autres endroits du conducteur, l’impédance sera réactive, soit capacitive, soit inductive, en fonction de l’avance ou du retard du courant sur la tension. En fait l’impédance suit les variations de l’impédance en dehors de la résonance des deux types de circuits résonnants précités. Le graphique schématise également le circuit électrique équivalent aux différents endroits de la longueur du conducteur (longueur électrique). Applications pratiques : - Un dipôle alimenté au centre, soit deux longueurs de 1/4 d’onde chacune alimentée par un conducteur de la ligne d’alimentation. Suivant les courbes de l’onde stationnaire de tension et de courant, l’impédance au point d’alimentation est faible (courant stationnaire élevé, tension stationnaire faible) et de nature résistive (circuit résonnant série). - Une antenne 5/8 d’onde alimentée à l’extrémité. 5/8 = 1/2 + 1/8. L’impédance à cet endroit, suivant les courbes des ondes stationnaires sera capacitive. Il aurait été préférable d’utiliser une longueur d’antenne de 3/4 d’onde pour obtenir une faible impédance résistive au point d’alimentation. Quoi qu’il en soit, si nous voulons conserver un brin rayonnant de 5/8 d’onde pour profiter de ses propriétés de rayonnement, nous introduisons une réactance inductive entre le point d’alimentation et le brin rayonnant de manière à neutraliser au point d’alimentation la réactance capacitive présente à la base du brin rayonnant. - Ainsi à l’aide des courbes de l’onde stationnaire de tension et de courant, il nous est toujours possible de déterminer la nature inductive ou capacitive de l’impédance à l’endroit où l’on désire connecter la ligne d’alimentation.

3. La ligne d’alimentation

La ligne d’alimentation que nous utilisons habituellement pour alimenter nos antennes est constituée mécaniquement de deux conducteurs étroitement couplés entre-eux, électriquement et magnétiquement. L’objectif principal de cette structure est d’annuler le champ électromagnétique éloigné résultant du rayonnement électromagnétique de chaque conducteur. 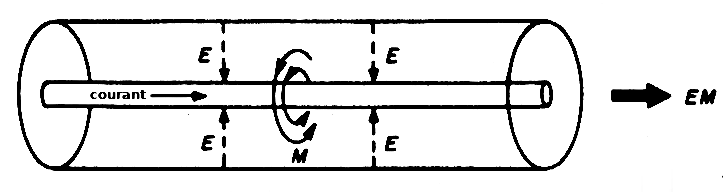Il existe deux formes principales de ligne d’alimentation, la ligne à conducteurs parallèles et la ligne à conducteurs concentriques, ou coaxiale. Sans entrer dans les détails, puisque le but ici est d’analyser le comportement des courants et des tensions le long de la ligne ; la ligne à fils parallèles est dite « symétrique », car elle est symétrique en courant et symétrique en tension. Comme si elle était alimentée par le secondaire d’un transformateur à point central mis à la masse. La ligne coaxiale est dite asymétrique car comme un des conducteur est mis à la masse, elle est forcément asymétrique en tension, mais il n’en reste pas moins qu’elle est symétrique en courant car les deux conducteurs étant étroitement couplés, les courants dans chaque conducteur ne peuvent que chercher à s’équilibrer à une même amplitude et sont déphasés de 180° comme dans un transformateur d’alimentation avec un rapport d’ enroulements primaire-secondaire de 1/1. Fermons cette parenthèse, pour définir la spécificité de la ligne que nous allons analyser.

3.1 Schéma électrique équivalent d’une ligne d’alimentation

Nous considérons ici une ligne parfaite, sans perte dissipative, qu’elle soit thermique ou par rayonnement, qui ne présente donc aucune atténuation de la tension et du courant sur la longueur de la ligne. (voir 1.1 où il est fait mention d’une atténuation (de l’eau) dont nous ne tenons pas compte ici) Remarque : Pratiquement toutes les lignes commerciales présentent des pertes qui sont renseignées habituellement par le fabricant comme « perte à l’adaptation » exprimée en dB par 100 pieds ou 30 mètres. De plus le fabricant spécifie cette perte en fonction de la fréquence utilisée. Il y lieu de ne pas confondre atténuation et impédance caractéristique qui elle ne change pas en fonction de la fréquence. La seule réalisation de ligne que l’on pourrait considérer sans perte est celle dite « Échelle à grenouilles » constituée de deux conducteurs parallèles séparés par l’air comme isolant. Une ligne d’alimentation parfaite peut être schématisée électriquement comme une succession de cellules LC, d’inductance L en série, et de capacité C en parallèle. L’inductance L étant l’inductance par unité de longueur de chaque conducteur et la capacité C, la capacité par unité de longueur de ligne. Si la présence d’une inductance série est facilement comprise, la capacité parallèle provient du fait que les deux conducteurs sont séparés par un isolant et soumis en tout point à une polarité de signe opposé. Nous retrouvons ainsi le comportement électrique d’un condensateur.

3.2 Impédance caractéristique de la ligne

Quand nous appliquons une source de puissance P = V x I à l’entrée de la ligne, dans un premier temps, la première cellule LC va se charger, puis se décharger pour charger la cellule suivante et ainsi de proche en proche. Ainsi le courant et la tension de charge-décharge reste à la même valeur tout au long de la ligne puisque les cellules sont identiques et sans perte. L’analyse mathématique nous permet de calculer l’impédance de la ligne en n’importe quel point de sa longueur, soit le rapport de la tension au courant qui est identique en tout point : dans laquelle

Z0 est l’impédance caractéristique ou suivant les goûts et les couleurs, l’impédance itérative, elle se répète indéfiniment ou encore l’impédance de charge (de la cellule LC) L est l’inductance par unité de longueur, C la capacité par unité de longueur.

Rappelons que c’est une impédance non dissipative, il n’y a pas de terme en R ! De plus, l’absence du terme « ω » faisant référence à la fréquence, nous indique que l’impédance caractéristique est indépendante de la fréquence. Exemple : Une ligne d’alimentation, sans perte, d’impédance caractéristique  Z₀ = 50 Ω alimentée par une source de puissance de 100 W sera le siège en chaque point de sa longueur d’une différence de potentiel de et d’un courant de

3.3 La ligne d’alimentation est adaptée à sa sortie

La ligne d’alimentation a pour fonction d’alimenter, dans les meilleures conditions, la charge, c-à-d l’antenne, à l’aide de toute la puissance disponible à la sortie de l’émetteur.

3.3.1 L’adaptation d’impédance

L’adaptation, se réfère à l’adaptation entre les deux impédances situées de part et d’autre de la jonction entre deux circuits, de manière à assurer un transfert sans perte de puissance de part et d’autre de la jonction. L’adaptation en sortie consiste à faire « correspondre » [*] l’impédance de la charge, l’impédance d’entrée de l’antenne, à l’impédance caractéristique de la ligne d’alimentation. La ligne d’alimentation ayant deux extrémités, une autre adaptation doit être effectuée, l’adaptation en entrée. L’adaptation en entrée consiste à faire « correspondre » [*] l’impédance caractéristique de la ligne d’alimentation à l’impédance demandée par la sortie de l’émetteur de manière à lui permettre de  délivrer sa puissance maximale. [*] Plus précisément, étant donné que les impédances en présence sont souvent complexes, de la forme Z = R ± jX  il convient alors de parler d’ « adaptation conjuguée » où les composantes résistives doivent être égales et où l’amplitude des composantes réactives doit aussi être la même, mais de nature opposée, soit inductive pour l’une et capacitive pour l’autre de manière à les annuler et atteindre la résonance à la seule fréquence considérée. Pour adapter Z₁ = R₁ + jX₁ à Z₂ = R₂ + jX₂  il faut X₂ = —X₁ et R₁ = R₂ Note : l’adaptation parfaite d’impédance sur une largeur de bande de fréquences n’est pas possible sans la possibilité d’un ajustement continu de l’une des deux réactances, comme un condensateur variable. Pour tirer le maximum de puissance qu’un générateur est capable de fournir à une charge, un calcul simple nous indique que l’impédance de la charge doit être égale à l’impédance de sa résistance interne. Z_L = Z_S dans laquelle :

Z_L est l’impédance de la charge ZS est l’impédance interne du générateur

Exemple : Adaptation en entrée : Si notre émetteur demande une impédance de charge de 50 Ω à sa sortie pour délivrer sa puissance maximale et que nous y connectons une ligne d’alimentation d’impédance caractéristique de 50 Ω nous aurons adapté la ligne à l’émetteur, à l’entrée, la jonction émetteur-ligne. Adaptation en sortie : A la sortie de la ligne de 50 Ω, si nous y connectons une charge de 50 Ω nous aurons également réalisé l’adaptation d’impédance à la sortie, la jonction ligne-charge. Ainsi la ligne d’alimentation est adaptée de bout en bout et toute la puissance disponible à l’émetteur, transmise via la ligne sans perte, se retrouve aux bornes de la charge, qui va dissiper cette puissance sous une forme thermique ou rayonnante. Par contre si la charge présente une impédance ZL = RL + jXL il est nécessaire d’insérer entre la charge et la ligne d’alimentation un circuit LC de valeur appropriée pour amener l’impédance de la  charge à apparaître égale à l’impédance caractéristique de la ligne d’alimentation. Regardons d’un peu plus près ce qui se produit à la sortie de la ligne. Chaque cellule LC de la ligne, transfère la puissance reçue de la cellule précédente à la cellule suivante de même impédance sans se soucier de ce qu’elle va en faire, et ce tout au long de la chaîne des cellules. La dernière cellule, juste avant la charge sans connaître la nature de celle-ci va faire de même. Si cette charge présente la même impédance, le même rapport tension/courant, que les autres cellules, toute la puissance va être absorbée par la charge comme si c’était la cellule suivante de la ligne et va être dissipée par celle-ci, ce qui est la fonction recherchée par une charge dissipative. Dans ce cas précis la puissance, comme la tension et le courant dans la ligne progressent dans un seul sens, de la source vers la charge. Nous sommes en présence d’une seule paire d’ondes progressives, celle de tension et celle de courant, incidentes à la charge, et donc suivant ce qui a été expliqué plus haut, il ne peut y avoir d’onde stationnaire sur la ligne. Schématiquement ce mode de fonctionnement revient à connecter directement la charge à l’émetteur, la ligne d’alimentation n’étant qu’un « transporteur » transparent, sans aucun effet sur la puissance transportée et ses composantes de tension et de courant.

3.4 La ligne d’alimentation n’est pas adaptée à sa sortie

L’impédance de la charge à la sortie diffère de l’impédance caractéristique de la ligne d’alimentation. Deux cas extrêmes et un cas intermédiaire peuvent se présenter :

1. la ligne d’alimentation est ouverte à sa sortie
2. la ligne d’alimentation est en court-circuit à sa sortie
3. une charge dont l’impédance dans un état intermédiaire entre les deux précédentes situations.

3.4.1 La ligne d’alimentation est ouverte à sa sortie

Nous pouvons facilement comprendre le comportement de ce type de ligne en retournant à : «  cfr 2. Un conducteur de longueur finie ouvert à son extrémité » Cependant, il y a lieu d’insister sur : - L’amplitude de la tension et du courant réfléchi, à la sortie, sont de la même amplitude que la tension et le courant incident. Ce qui par le simple calcul de leur produit, nous informe que + toute la puissance incidente est entièrement réfléchie par la sortie ouverte. L’évolution de l’impédance le long d’une ligne ouverte, nous indique qu’en fonction de la distance où l’on se situe par rapport à la sortie, distance exprimée en longueurs d’onde, l’impédance en chaque point peut être très différente de l’impédance caractéristique de la ligne. Elle est caractérisée par le rapport en amplitude et en phase de l’onde stationnaire de tension à l’onde stationnaire de courant. Il en est de même à l’entrée de la ligne, à la jonction émetteur-ligne où l’émetteur risque d’être confronté à une impédance très différente de l’impédance caractéristique de la ligne. Sans précautions particulières une désadaptation en sortie entraîne toujours une désadaptation à l’entrée. 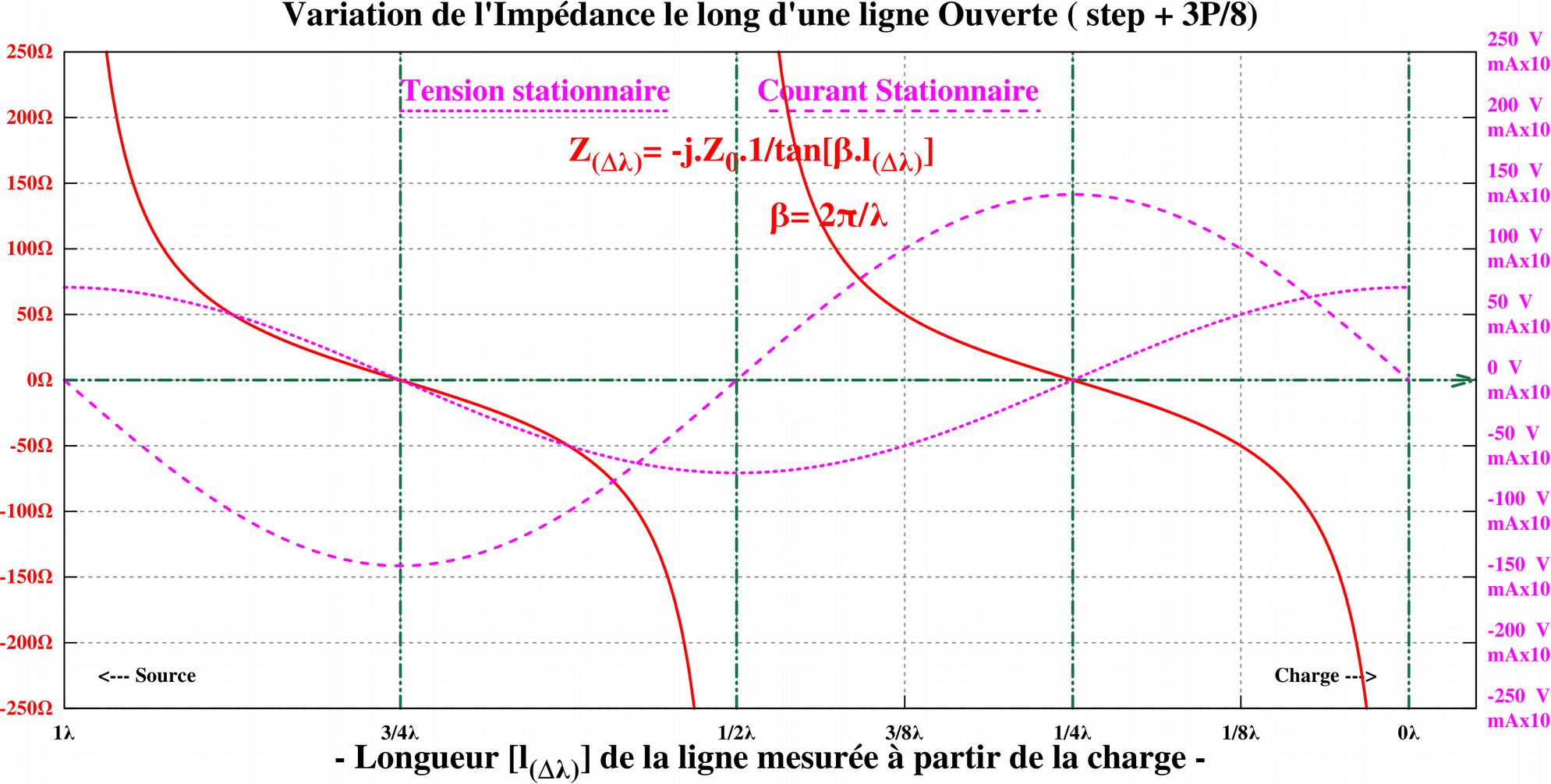Note : attention que les tensions et courants incidents et réfléchis, une fois situés sur la ligne d’alimentation ne sont concernés que par l’impédance caractéristique de la ligne d’alimentation. Exemple d'utilisation Une longueur électrique de 1/4 d’onde à sortie ouverte présente une basse impédance à son entrée et peut donc servir comme par exemple une terre artificielle mono-fréquence pour un équipement radio situé à l’étage de l’habitation

3.4.2 La ligne d’alimentation est en court-circuit à sa sortie

Le principe de fonctionnement reste le même que pour une ligne d’alimentation ouverte à sa sortie. La seule différence est qu’en fin de ligne, c’est la tension qui va chuter à zéro et induire suivant la loi de Lenz un courant induit de même amplitude et en phase avec le courant incident. Ce courant induit va se déplacer en retour vers l’entrée de la ligne. Ce qui va construire l’onde progressive réfléchie de courant. Les 5 graphiques suivants reproduisent la progression de l’onde progressive incidente et réfléchie de courant, sur une 1,3/4 de période par pas de 1/8 de période ainsi que la formation de l’onde stationnaire de courant correspondante.    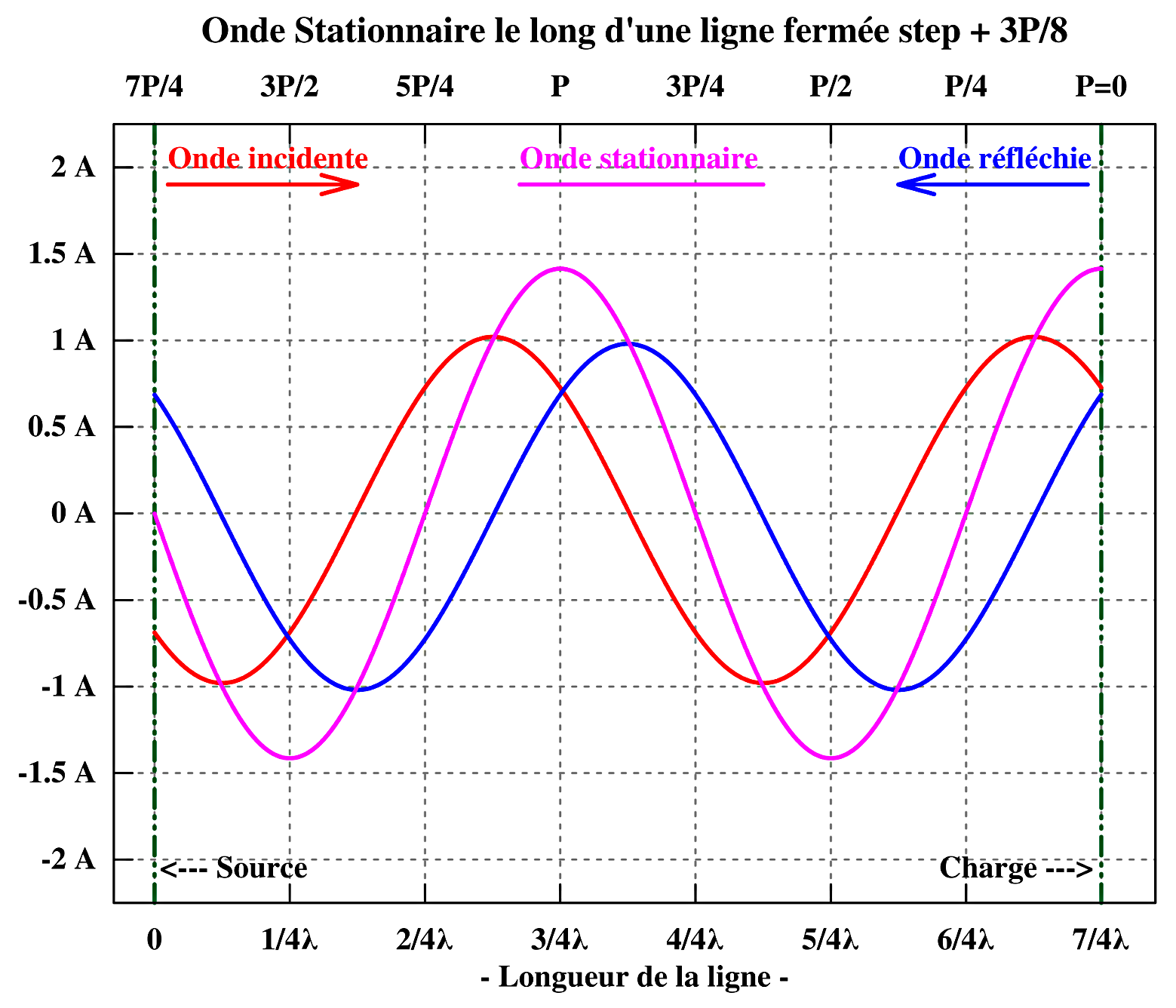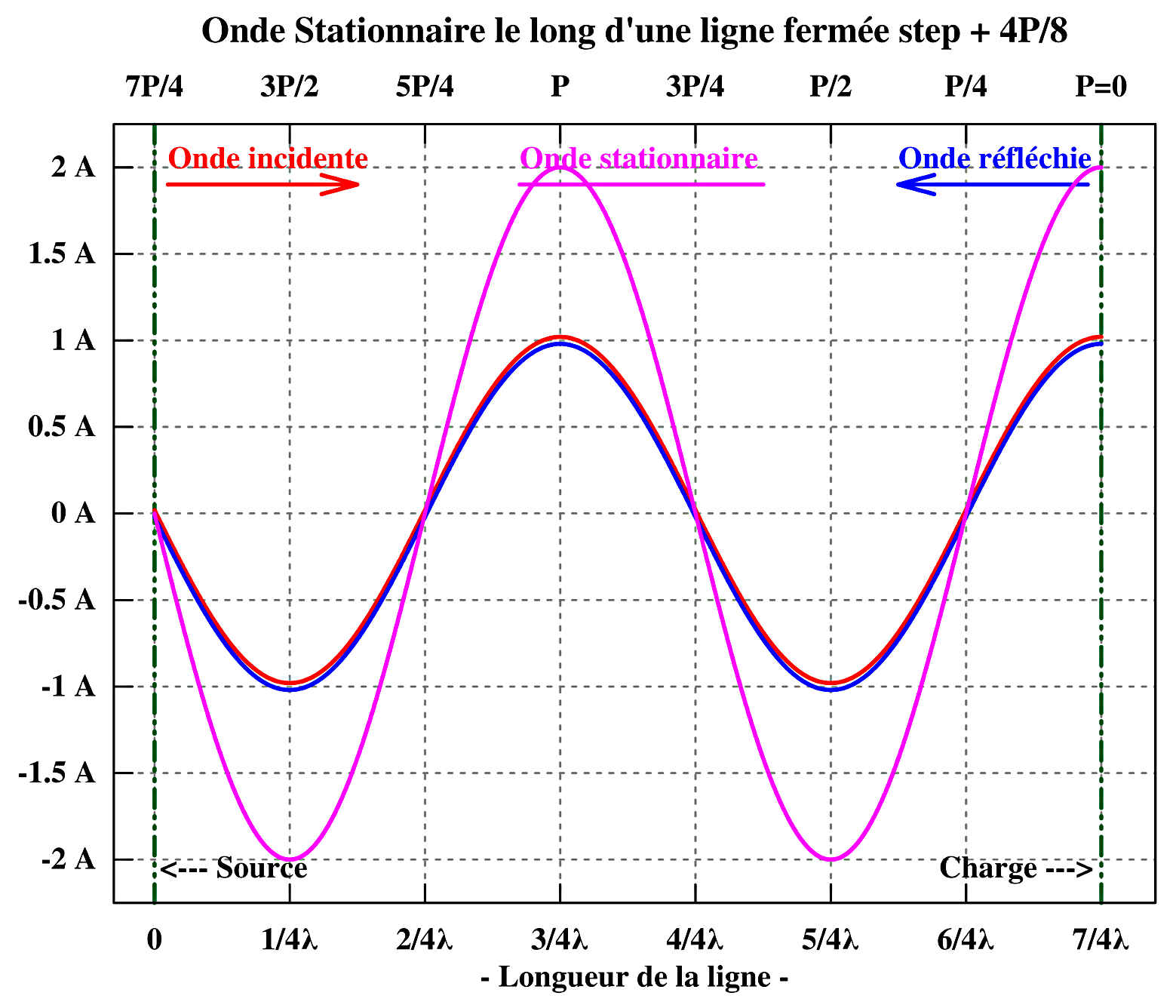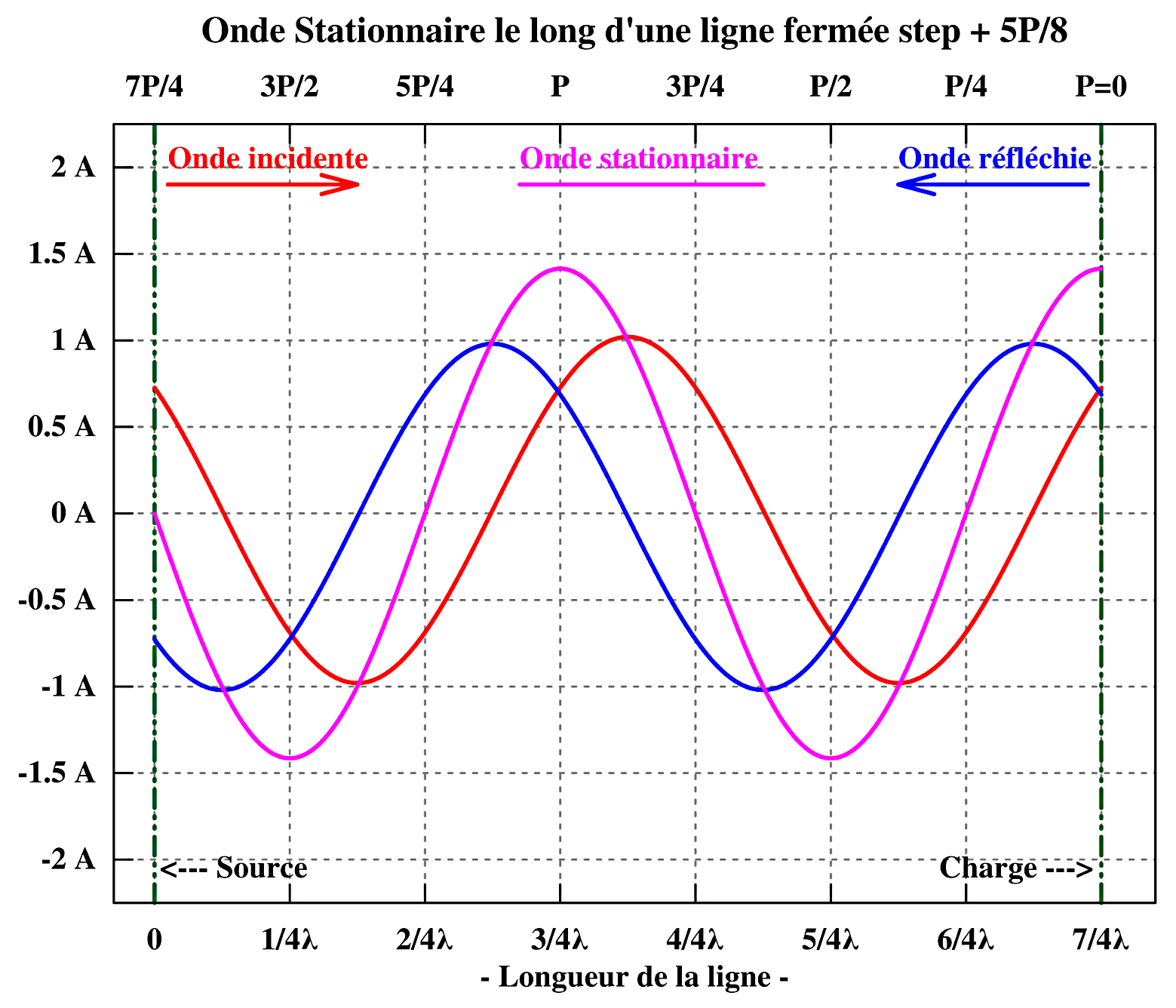         Quant à la tension on peut supposer, sans entrer dans les détails de l’interaction des champs électrique et magnétique, qu’il existe à cet endroit une tension induite de même amplitude mais de phase opposée à la tension incidente, de manière à annuler toute tension au niveau du court-circuit et cette tension induite va se propager en retour vers l’entrée. Ce qui va construire l’onde progressive réfléchie de tension. 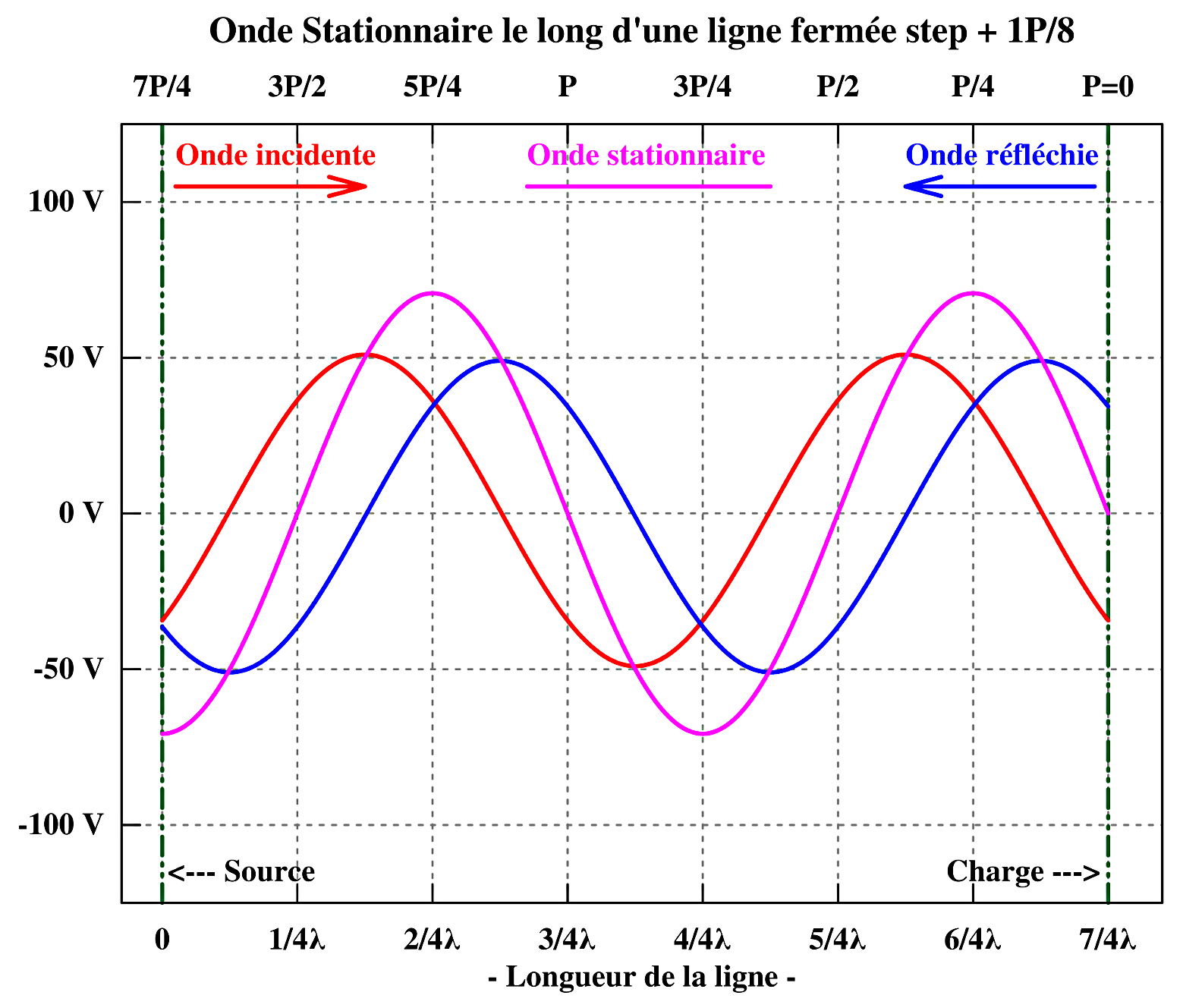Les 5 graphiques reproduisent la progression de l’onde progressive incidente et réfléchie de tension, sur une 1,3/4 période par pas de 1/8 de période ainsi que la formation de l’onde stationnaire de tension correspondante.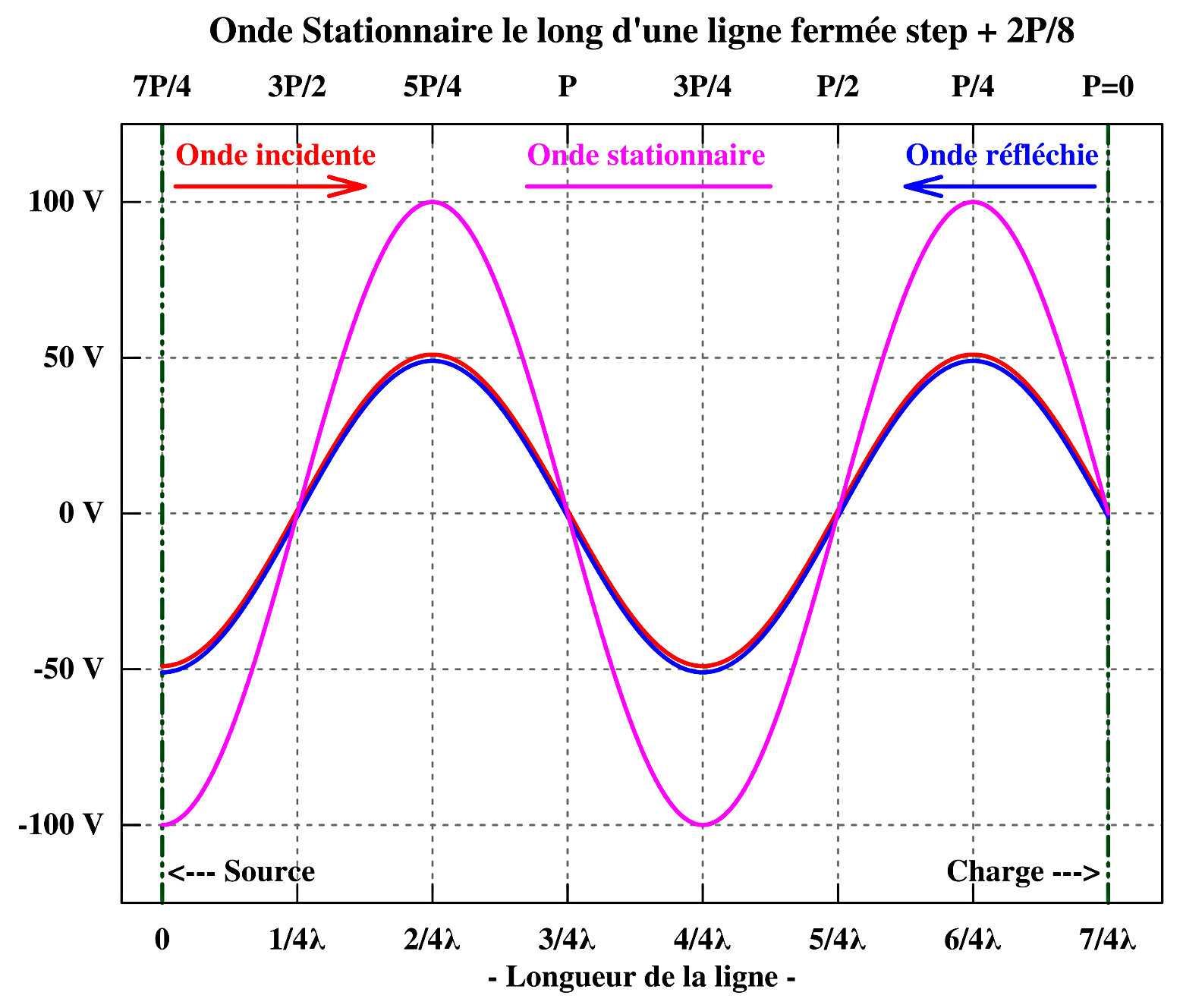    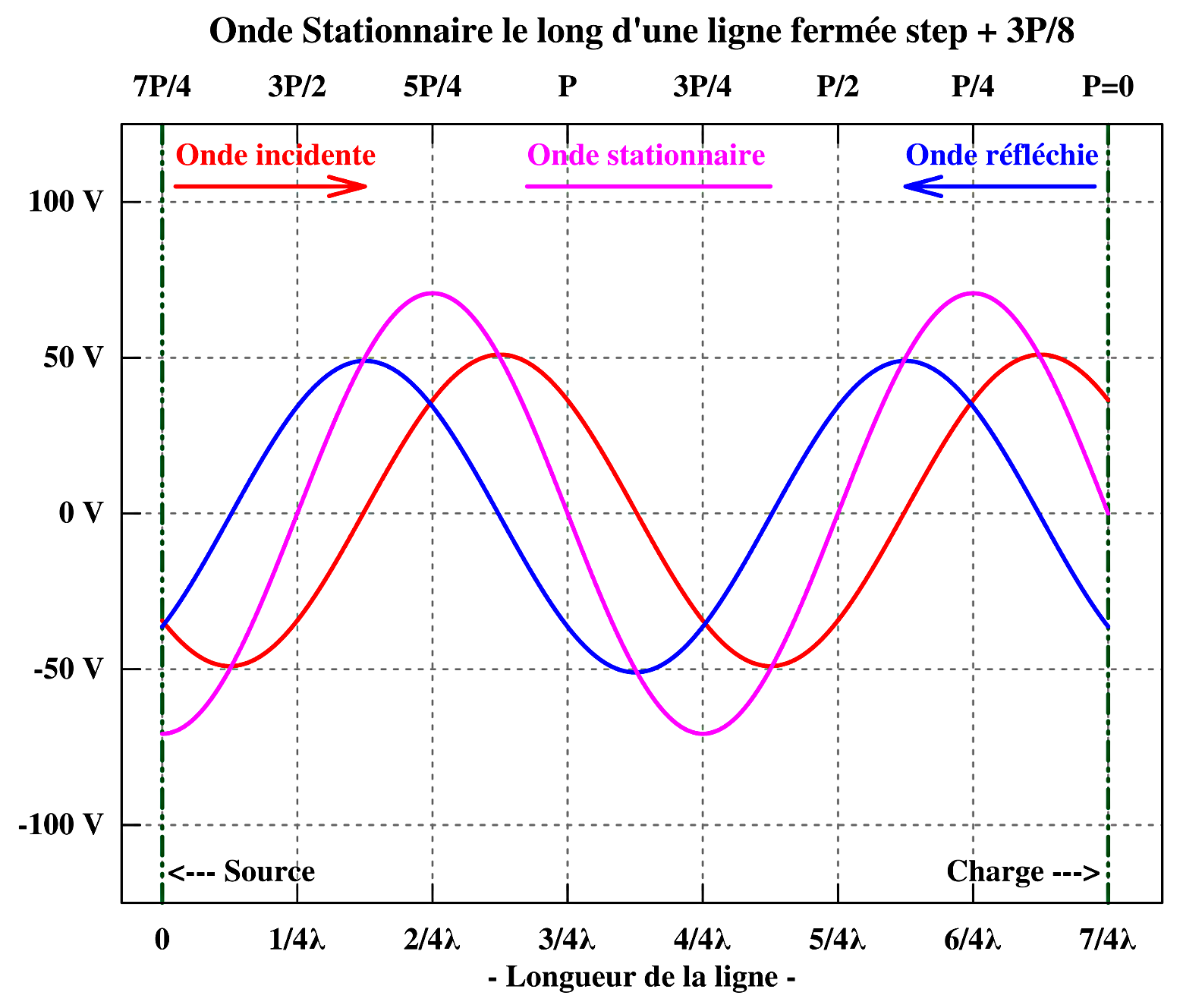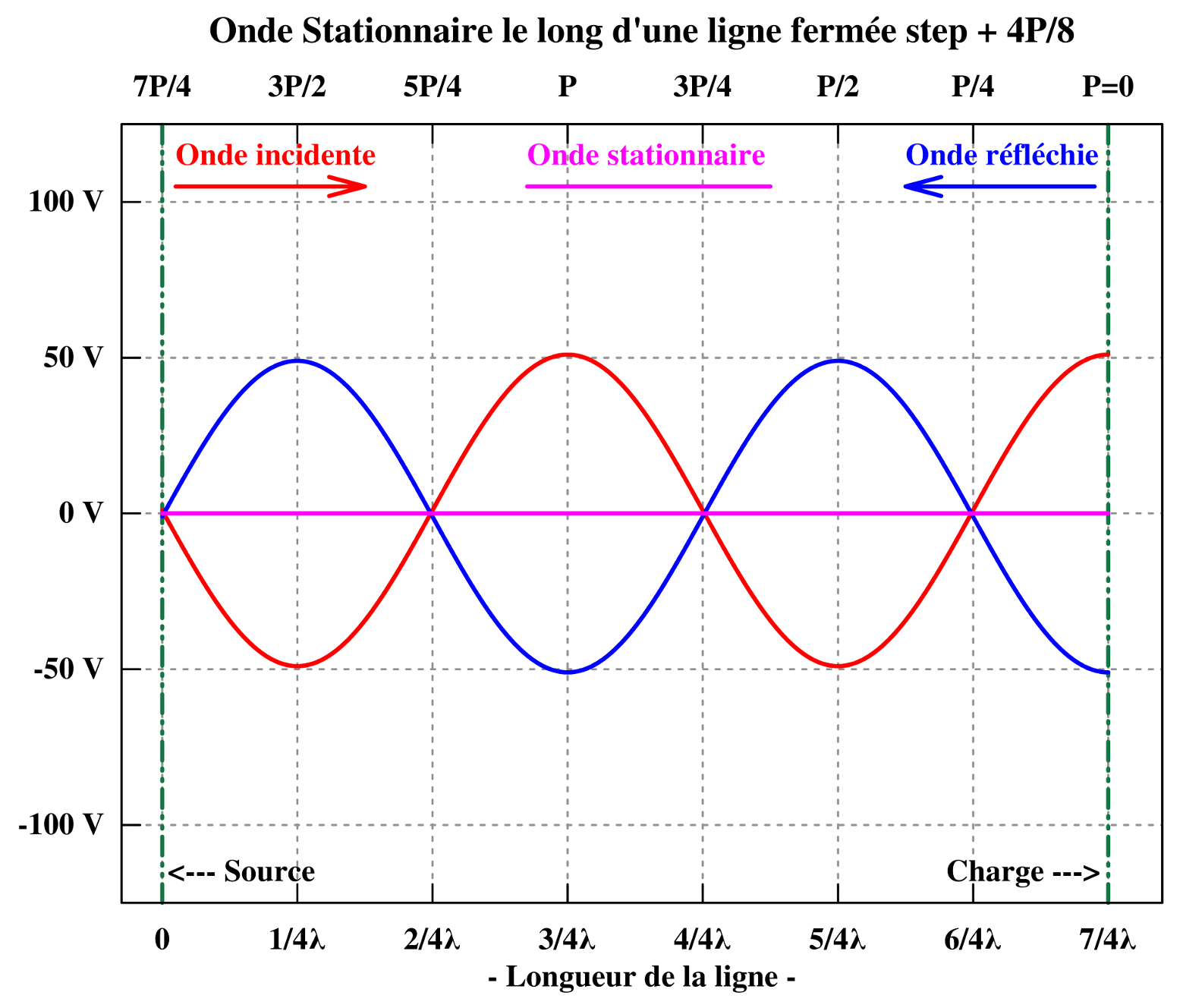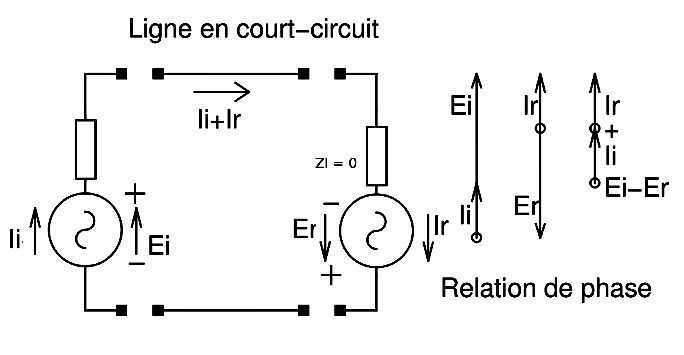         La schématique électrique reste la même, l’extrémité en court-circuit d’une ligne d’alimentation peut être représentée par un générateur de puissance réfléchie dont la tension est de même amplitude que la tension incidente, mais dont la phase est inversée de 180°, de quoi annuler toute tension à cet endroit et dont le courant est de même amplitude et en phase avec le courant incident.  L’amplitude de la tension et du courant réfléchis étant la même que celle de la tension et du courant incidents, la puissance réfléchie, c-à-d le produit des deux composantes électriques est égal à la puissance incidente et ainsi la réflexion de puissance est totale. Les graphiques ci-dessous représentent la variation d’amplitude sur plusieurs cycles complets de l’onde stationnaire de tension et de l’onde stationnaire de courant. De même que pour la ligne ouverte à sa sortie, l’évolution de l’impédance le long d’une ligne en court-circuit, nous indique qu’en fonction de la distance où l’on se situe par rapport à la sortie, distance exprimée en longueurs d’onde, l’impédance est différente de l’impédance caractéristique de la ligne, mais est toujours le rapport en amplitude et en phase de l’onde stationnaire de tension à l’onde stationnaire de courant. Il en est ainsi de même à l’entrée de la ligne, à la jonction émetteur-ligne, l’émetteur risque d’être confronté à une impédance très différente de l’impédance caractéristique de la ligne. 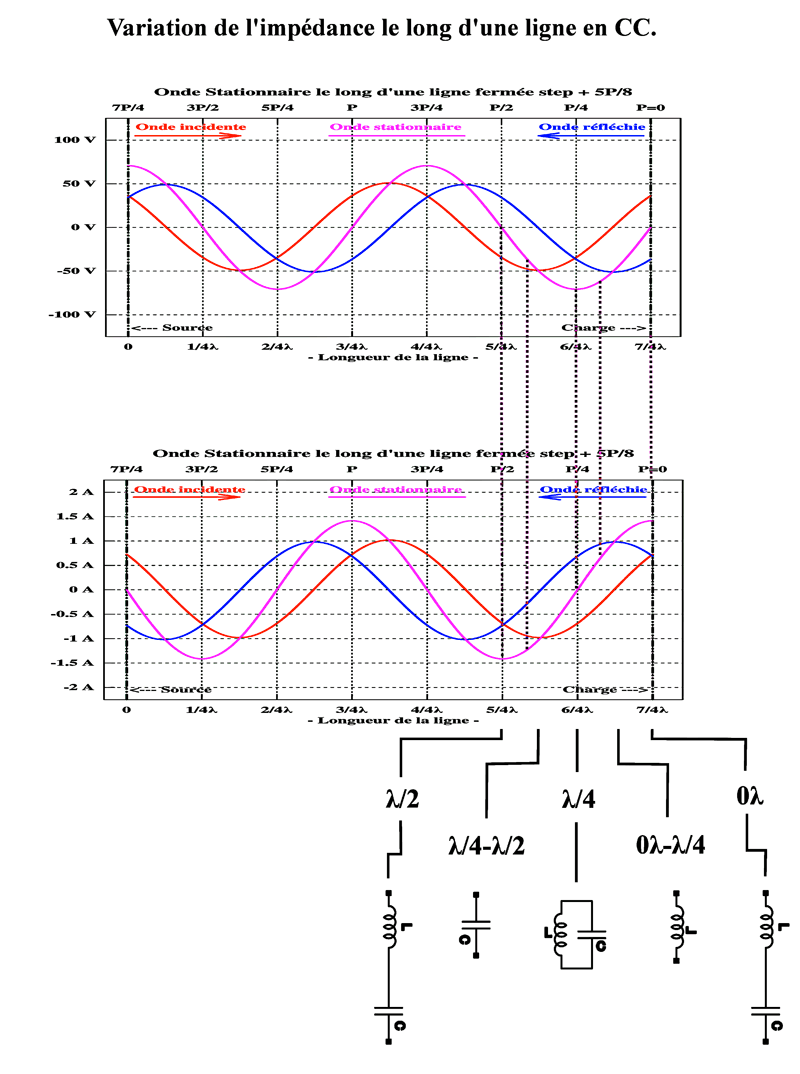Exemple de l’utilisation d’une ligne en court-circuit à sa sortie Supposons que notre émetteur produise une harmonique 2 de sa fréquence d’émission insuffisamment atténuée, atténuation inférieure à 60 dB. Comment atténuer, sans « charcuter » l émetteur, cette fréquence harmonique sans trop perturber la fréquence fondamentale émise ? Simplement en insérant n’importe où sur la longueur du coax, comme exemple de ligne, un connecteur en « T » dont les bras longitudinaux assurent la continuité de la ligne d’alimentation. Sur le troisième connecteur du « T » il « suffit » alors d’insérer un tronçon de ligne en court-circuit en sortie de 1/4 d’onde électrique de la fréquence fondamentale. Ce tronçon de ligne à basse impédance en sortie en court-circuit, va offrir une haute impédance à son entrée au niveau du « T ». Pour l’harmonique 2, la longueur électrique de 1/4 d’onde devient une demi-onde et offre une basse impédance à son entrée au niveau du « T » ayant pour conséquence de « court-circuiter » l’harmonique 2 et ainsi arrêter son trajet vers la charge en sortie. Le mécanisme de l’annulation de la réflexion des ondes sur une ligne de transmission, par l’utilisation d’un « Stub » d’adaptation, un tronçon de ligne de longueur déterminée, pour « arrêter » l’onde réfléchie par la désadaptation d’impédance à la jonction ligne-antenne est un sujet tellement passionnant qu’il encombrerait trop l’espace réservé au présent sujet.

3.4.3 La ligne d’alimentation est chargée par une impédance différente de son impédance caractéristique

C’est une situation intermédiaire entre les deux situations précédentes. La charge n’est pas nulle, ni infinie et la puissance réfléchie est alors la différence entre la puissance incidente et la puissance absorbée par la charge.  Il en résulte que si l’impédance de la charge est supérieure à l’impédance caractéristique de la ligne d’alimentation, le mode de fonctionnement sera similaire à la ligne ouverte en sortie, avec des valeurs d’amplitude moindre pour la tension et le courant réfléchis. De la même manière si l’impédance de la charge est inférieure à l’impédance caractéristique de la ligne, le comportement sera semblable à celui de la sortie en court-circuit, toujours avec des amplitudes moindres de la tension et du courant réfléchis.   Formation de l’onde stationnaire de tension pour une ligne de 50 Ω avec en sortie une charge de 120 Ω. La tension incidente Vi = 50 v La tension réfléchie Vr = 20,59 v L’amplitude de l’onde stationnaire de tension : 0 λ est l’extrémité charge. à 0 λ :  Vi + Vr = 70.59 v à 1/4 λ : Vi - Vr = 29,41 v à 1/2 λ : Vi + Vr = 70.59 v (inversion de phase) à 3/4 λ : Vi - Vr = - 29,41 v à 1 λ :  Vi + Vr = - 70.59 v     Répartition de l’amplitude l’onde stationnaire de tension sur une distance de 1,3/4 d’onde à partir de la charge pendant plusieurs cycles de la fréquence.               Répartition de l’amplitude l’onde stationnaire de  courant sur une distance de 1,3/4 d’onde à partir de la charge pendant plusieurs cycles de la fréquence. Le courant incident Ii = 1 A Le courant réfléchi Ir = 0,41 A L’amplitude de l’onde stationnaire de courant: 0 λ est l’extrémité charge. à 0 λ :  Ii - Ir = 0.59 A à 1/4 λ : Ii + Ir = 1.4 1A à 1/2 λ : Ii - Ir =  0,59 A à 3/4 λ : Ii + Ir = 1,41  A à 1 λ :  Ii + Ir = 0.59 A L’impédance de la ligne en chaque point se calcule comme le rapport de l’onde stationnaire et de l’onde stationnaire en ce point :   Exemple :

à à 0 λ :           Z = 79,59 V / 0,51 A = 40,59 Ω à 1/4 λ :           Z = 29,41 V / 1,41 A = 41,47 Ω à 1/2 λ :           Z = 79,59 V / 0,51 A = 40.59 Ω à 3/4 λ :           Z = 29,41 V / 1,41 A = 41,47 Ω à 1 λ :                Z = 79,59 V / 0,51 A = 40,59 Ω

 

4. Le R.O.S. et tout ça, tout ça

Le R.O.S. chiffre le rapport entre la valeur maximum de l’amplitude de l’onde stationnaire de tension située en un point du conducteur et sa valeur minimum située à 1/4 longueur d’onde du premier. Le R.O.S signifie Rapport d’Onde Stationnaire et pour les radioamateurs anglophones, la dénomination correspondante est le V.S.W.R. Voltage Standing Wave Ratio ou le rapport d’onde stationnaire de tension. Note : Ce n’est donc pas un T.O.S, un Taux d’onde stationnaire, car le taux est une grandeur qui fait référence au nombre 100, c’est un pourcentage. En se référant aux graphiques ci-avant, la tension maximale de l’onde stationnaire de tension V_sta.max se situe sur le conducteur à l’endroit où l’amplitude de crête de la tension incidente V_p.inc et de la tension réfléchie V_p.ref  sont en phase. On obtient donc :  V_Sta.max = V_p.inc + V_p.ref De même, le minimum de l’amplitude de l’onde stationnaire de tension V_Sta.min se situe sur le conducteur à l’endroit où l’amplitude de crête de la tension incidente V_p.inc et de la tension réfléchie V_p.ref sont en opposition de phase. On obtient donc :   V_Sta.mn = V_p.inc — V_p.ref L’expression générale du R.O.S est :  (1) Expression mathématique qui nous oblige à connaître l’endroit sur le conducteur où la tension est maximale et l’autre endroit où elle est minimale pour pouvoir les mesurer. Très peu intéressant Développons la deuxième partie de l’équation (1)  ci-dessus. 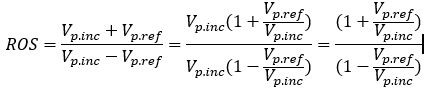 représente le rapport de la tension réfléchie à la tension incidente. Il nous dit de combien de fois la tension réfléchie est inférieure à la tension incidente. Il est toujours compris entre 0 et 1. Quand toute la tension incidente est réfléchie le rapport (V_p.ref / V_p.inc )= 1 Quand aucune tension n’est réfléchie, à l’adaptation, le rapport (V_p.ref / V_p.inc ) = 0 Ce rapport est le même en ce qui concerne le courant réfléchi et le courant incident, puisque les deux partagent l’impédance caractéristique commune de la ligne d’alimentation. Ce rapport est symbolisé par la lettre grec ρ (rho)  Coefficient de réflexion en tension ou en courant De ce qui précède, l’équation du ROS se simplifie comme :  Exemple : Un ampère-mètre directionnel placé à la jonction antenne de la ligne d’alimentation, mesure un courant incident de 1,5A et un courant réfléchi de 0,5 A. Ce qui nous donne le coefficient de réflexion en courant :  Qui permet de calculer le ROS : Sachant que P = V x I  le produit du coefficient de réflexion en tension et du coefficient de réflexion en courant donne le coefficient de réflexion de puissance. Dans l’exemple   Un peu moins d’un dixième de la puissance incidente est réfléchie. Une autre information importante peut être déduite de la valeur du R.O.S. C’est le rapport entre l’impédance de la charge, ou l’impédance d’entrée de l’antenne, et l’impédance caractéristique de la ligne d’alimentation. Le coefficient de réflexion en tension ou en courant est également défini mathématiquement en fonction de l’impédance de la charge et de l’impédance caractéristique de la ligne d’alimentation [*]  : sous la forme :   Plus simplement énoncé, sur base de l’impédance caractéristique de la ligne d’alimentation et du R.O.S, soit directement par la lecture du ROS-mètre ou par la mesure du courant incident et réfléchi, il est possible de connaître la valeur de l’impédance de charge ou d’entrée de l’antenne au moyen de l’équation suivante Nous remplaçons dans l’équation (3) ρ par sa valeur donnée par l’équation (4) 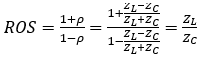 L’impédance de la charge étant généralement complexe, c’est le module que le ROS nous permet de trouver. [*] : A l’aide des mathématiques supérieures il est possible d’établir deux équations que l’on appelle les équations fondamentales d’une ligne sans perte qui permettent de calculer la tension et le courant en tout point d’une ligne d’alimentation en fonction de sa distance à la charge, du courant dans la charge et de la tension à ses bornes. A partir de ces équations l’impédance en tout point de la ligne peut être calculée, mais également le coefficient de réflexion en tension-courant en n’importe quel point. Le coefficient de réflexion en tension s’établit comme : Avec  

ZL : l’impédance de la charge Z_L = R_L +- j_XL ZC : l’impédance caractéristique de la ligne d’alimentation  Z_c = R_c ± j_Xc ou Z_c = R_c x : la distance du point considéré à la charge e : la base du logarithme népérien : 2,71828... β : la constante de phase 2π/λ  λ : la longueur d’onde de la fréquence utilisée

Dans l’exemple nous calculons le coefficient de réflexion à la charge, donc pour x=0 et donc : 

5. La ligne avec perte

Jusqu’ici nous avons considéré uniquement une ligne d’alimentation sans perte et calculé les différents paramètres à partir des valeurs tension et courant à la sortie charge de la ligne. Comme dans les exemples « des ronds dans l’eau » nous n’avons pas tenu compte de l’amortissement par unité de longueur du trajet des ondes. Comme rien n’est parfait en ce bas monde, nous allons faire intervenir l’atténuation de la ligne par longueur de ligne comme stipule le fabricant : Un exemple chiffré est plus intuitif : Nous sélectionnons une ligne d’alimentation d’impédance caractéristique 50 Ω et présentant 2 dB d’atténuation pour les 30 mètres installés. La puissance fournie par l’émetteur à l’entrée est de 100 W soit 20 dBw. À la sorte des 30 m il reste 20 dB – 2dB = 18 dBw soit 63 W Si la charge est de 50 Ω, ces 63 W sont dissipés et il n’y a pas de puissance en retour. Le ROS = 1/1 Si maintenant la charge est de 150 Ω, le ROS à la sortie est 3:1 ROS= 150/50 = 3 Le coefficient de réflexion en tension ou en courant est (3-1) / (3+1) = 1/2 Le coefficient de puissance est ρ² = 1/4 La puissance réfléchie au départ de l’antenne est 63 W / 4 = 16 W La puissance rayonnée par l’antenne est : 63 W -16 W = 47 W La puissance réfléchie à l’entrée en fonction de l’atténuation est de 16 W / 4 = 4 W Le coefficient de puissance de réflexion à l’entrée est ρ2 = 4/100= 1/25 Le coefficient de réflexion en tension ρ = 1/5 Le ROS sur le mesureur que je place à l’entrée le ROS est 1.5:1  ROS  (1+1/5) / (1- 1/5) = 1,5 Magnifique, j’ai un bon TOS et mon installation est performante !!?? Il y a beaucoup plus a dire, notamment si l’on place une « black-box » « miiiiracle » entre l’émetteur et la ligne d’alimentation. C’est une autre aventure. Un bon sujet pour vos prochains QSOs radioamateurs.

73s de Yvan-on4cy

Le lien pour télécharger cet article au format PDF :