E = mc² : Comment comprendre cette équation d’Albert Einstein ?

Introduction :

L’équation E = mc² est une relation d’équivalence entre la masse et l’énergie où « E » est l’énergie en Joule [J], « m » est la masse en kilogramme [kg] et « c » est la vitesse de la lumière en mètre par seconde [m/s].

Cette équation est la plus célèbre dans le monde : tout le monde connaît cette équation, tout le monde sait qu’elle a été découverte par Albert Einstein et la plupart d’entre nous savent que cette équation a été découverte en 1905 lorsqu’Albert Einstein a publié ses travaux sur la théorie de la relativité restreinte (la vitesse de la lumière est constante, même si la source de celle-ci se déplace). Cette théorie sera étendue par Albert Einstein à la relativité générale (théorie relativiste sur la gravitation) en 1915.

Comment donc comprendre cette équation à l’apparence d’une simplicité déconcertante et qui ne comporte que quatre symboles : E, m, c et 2 ? Pour réponde à cette question, il y a lieu de commencer par bien comprendre ce qu’est l’énergie, ce que c’est la masse, admettre une fois pour toute que la lumière va toujours à la vitesse de la lumière dans le vide et que cette vitesse est non seulement constante d’une manière universelle mais aussi qu’il s’agit de la vitesse limite maximale dans notre univers. N’en déplaise aux amateurs de science-fiction : non, il n’y a pas moyen de se déplacer à une vitesse supérieure à celle de la lumière comme le vaisseau spatial « Falcon Millenium » dans les épisodes « Star Wars » de Georges Lucas.

Pour comprendre l’équivalence entre la masse et l’énergie, il faudra effectuer un voyage vers l’infiniment petit, c’est-à-dire au niveau de l’atome, des particules élémentaires qui le composent et des interactions qui existent entre ces particules. Nous entrerons ainsi dans le domaine de la physique quantique. Le mot « quantique » signifie ici une quantité à valeur discrète (valeur finie ou dénombrable). Par exemple, un dé cubique ne comprend que les valeurs 1, 2, 3, 4, 5 et 6. Dans un autre exemple : on peut acheter du beurre tant que l’on veut mais rien qu’en quantités bien définies : un quart de beurre (¼ de kg) ou une livre de beurre (livre anglaise = 453 g ou livre métrique = 500 g).

Qu’est-ce que la masse ?

Le concept de masse nous est familier car il est associé à une quantité de matière (substance) d’une densité donnée et contenue dans un volume donné par les dimensions d’un objet. Nous verrons que cette définition de la masse, établie sur une corrélation avec une quantité de matière n’est pas exacte car elle est liée à une quantité d’énergie selon l’équation d’Einstein écrite sous sa forme originelle :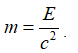

On verra ensuite que ce concept de masse doit être élargi depuis la prédiction théorique du boson de Higgs-Englert en 1964 et sa découverte en 2012 au LHC (Large Hadron Collider) du CERN (Conseil Européen pour la Recherche Nucléaire) à Genève.

Dire que la masse correspond à une quantité d’énergie est tout-à-fait contre-intuitif, mais quand on s’attaque à la physique, il faut s’habituer à penser contre son cerveau car la physique explique le possible, c’est-à-dire le comportement réel de la nature, par l’impossible, c’est-à-dire des lois physiques qui vont à l’encontre de nos intuitions.

En d’autres mots, les lois de la physique qui contredisent l’observation en apparence obligent à réinterpréter ce que l’on voit d’une façon différente. En effet, on a du mal à imaginer ce que pourrait être une particule de matière qui ne serait pas massive et on a du mal à imaginer ce que serait de la masse qui ne serait pas incarnée en particules de matière.

Qu’apprend-on à l’école au sujet de la masse ? Il s’agit d’une grandeur mesurable : on peut effectuer des mesures qui donnent la masse d’un corps dans une certaine unité qui est le kilogramme (kg). Attention, la masse n’est pas le poids : le poids est une force qui s’exprime en Newton [N] et qui est liée à la gravité qui s’applique à toute masse. La gravité est liée à l’accélération de la pesanteur. Le poids est le produit de la masse par l’accélération de la pesanteur : P = mg. La masse est aussi une grandeur mesurante (le mesurande ou résultat d’une mesure), c’est-à-dire que c’est une grandeur qui mesure quelque chose : le degré de substantialité d’un corps. Plus il y a de masse, plus il y a de substance, et donc plus il y a d’atomes.

Deux sortes de masses :

Newton comprend à la fin du XVII^ème siècle qu’il y a deux sortes de masse. D’une part il y a la masse pesante (ou masse grave, du mot « gravité ») qui est ce par quoi un corps, placé dans un champ de gravitation, subit la force de gravitation ; une sorte d’étiquette que porte un corps et par laquelle il est reconnu par la gravitation. D’autre part il y a une autre masse qui intervient dans la relation fondamentale de la dynamique : la force qu’on exerce sur un corps, quelle que soit l’origine de cette force, est égale au produit de sa masse par l’accélération qu’il subit. Il s’agit de la masse inertielle dans la relation de la dynamique : F = ma. Cette masse mesure l’inertie d’un corps, c’est-à-dire qu’elle mesure la difficulté qu’il y a à modifier le mouvement d’un corps, à l’interrompre si le corps est en mouvement ou le créer si le corps est immobile. Plus un corps a une masse inerte élevée, plus il est difficile de le mettre en mouvement.

Newton découvre que la masse pesante est égale à la masse inerte (inertielle) et qu’elle s’exprime dans la même unité (kg). Cela a comme conséquence que le mouvement d’un corps dans un champ de gravitation est complètement indépendant de sa masse. Ce qui confirme ce que Galilée avait déjà découvert : tous les corps tombent à la même vitesse (dans le vide) quelle que soit leur masse. Dans un autre exemple : la terre est en mouvement et tourne autour du soleil ; la terre se situe dans le champ de gravitation du soleil. Si l’on remplace la terre par une boule de pétanque, cette boule décrira exactement la même orbite que parcourt la terre autour du soleil ; la trajectoire de la boule de pétanque sera exactement la même que celle de la terre.

Au XX^ème siècle, Einstein va reprendre l’égalité entre la masse pesante et la masse inertielle et va postuler qu’il s’agit non pas d’une égalité mais d’une identité. L’inertie et la gravitation sont en quelque sorte la même chose et cela va le conduire à élaborer une nouvelle théorie de la gravitation que l’on appelle la relativité générale.

La vitesse de la lumière, vitesse limite que les corps massifs ne peuvent pas dépasser :

En mécanique newtonienne, l’inertie d’un corps est mesurée par sa masse : Inertie = I = m. Mais en relativité restreinte, l’inertie n’est plus égale à la masse du corps mais elle est égale à l’énergie totale du corps (l’énergie de masse) divisée par la vitesse de la lumière au carré :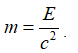

On parle ici d’une énergie de masse. Prenons quelques ordres de grandeur avec un corps qui a une masse de 1 g (10^-3 kg). La vitesse de la lumière est de 300 000 km/s (10⁸ m/s).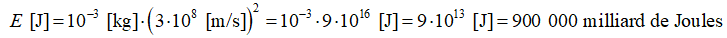

Ce qui donne une énergie de :

Un objet de masse « m » possède de l’énergie du seul fait qu’il a une masse.

En ce qui concerne l’inertie, celle-ci augmente avec la vitesse.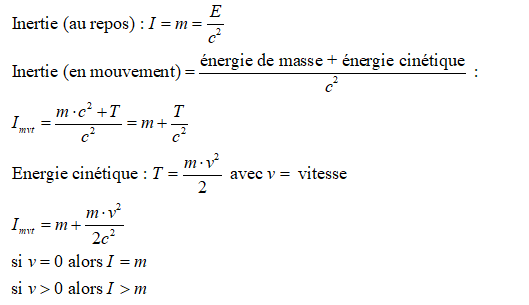

Énergie d’un corps en mouvement à vitesse « v » avec le facteur de Lorenz « γ » :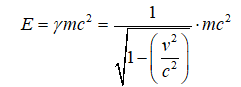

Si un corps ou une particule est en mouvement, l’énergie cinétique de cette particule va augmenter avec la vitesse et l’inertie de cette particule va donc aussi augmenter avec la vitesse. Plus la particule va aller vite, plus son inertie sera grande et plus il sera difficile de la faire aller plus vite jusqu’au moment où l’inertie sera tellement élevée qu’on ne pourra plus modifier la vitesse du corps ou de la particule. La formule ci-dessus implique donc l’existence d’une vitesse limite, c’est-à-dire une vitesse que les particules ne peuvent pas dépasser, c’est-à-dire qu’elles ne peuvent pas dépasser la vitesse de la lumière qui est égale à c. La lettre « c » vient du mot « célérité ».

Il y a donc un moment où on aura beau donner de l’énergie cinétique à une particule, on ne parviendra plus à augmenter sa vitesse. C’est ce que l’on réalise dans les accélérateurs de particules. Le mot « accélérateur » de particule est un abus de langage puisque précisément, on n’accélère pas les particules. Dans le LHC (Large Hadron Collider) on injecte des protons à une certaine énergie (par exemple 450 GeV). Ces protons se déplacent presqu’à la vitesse de la lumière et on leur donne de l’énergie, tour par tour, beaucoup d’énergie (3,5 TeV), et cela se fait à vitesse constante. Tout se passe comme si on « accélère » les protons à vitesse constante. En fait, on donne aux protons de l’inertie, c’est-à-dire de l’énergie, mais on ne leur donne pas d’accroissement de vitesse parce que les protons sont déjà à la vitesse maximale.

La vitesse de la lumière dans le vide, une constante universelle :

La lumière va à la vitesse de la lumière : 299 792 458 m/s. Il s’agit d’un invariant quel que soit le référentiel dans lequel on se trouve.

Au XVII^ème siècle, Newton énonce que la lumière est une mitraille de corpuscules qui se propagent dans l’espace. Au XIX^ème siècle, à la suite d’expériences menées en Angleterre par Thomas Young et en France par Augustin Fresnel, se développe l’idée que la lumière n’est pas un phénomène corpusculaire mais un phénomène ondulatoire parce qu’elle est capable de produire des interférences, un peu comme les cercles d’ondes à la surface de l’eau quand ces ondes se croisent. Cette idée va se trouver renforcée dans les années 1860 après qu’un physicien écossait qui s’appelle James Clerk Maxwell va proposer une théorie de l’électromagnétisme qui laisse voir qu’en effet, la lumière est bien un phénomène ondulatoire constitué d’ondes électromagnétiques qui se propagent dans l’espace à la vitesse de la lumière.

En août 1899, Albert Enstein pense que les forces électriques ne peuvent être définies correctement que dans un espace vide. En 1905, Einstein pense que la lumière est un phénomène physique autonome et qu’il n’y a pas besoin de milieu matériel pour la propagation de celle-ci : elle se propage dans le vide à la vitesse de la lumière. Cette vitesse de la lumière est un absolu : elle est la même dans tous les référentiels, elle ne dépend pas de la vitesse de la source qui l’émet et elle ne dépend pas non plus de la vitesse de l’observateur qui la mesure quelle que soit la vitesse à laquelle l’observateur se déplace dans l’espace. Le fait que la lumière va toujours à la vitesse de la lumière et que cette vitesse est un absolu va obliger Einstein à repenser les relations entre l’espace et le temps. Ce sera le contenu de sa théorie de la relativité restreinte.

C’est ainsi qu’Einstein amène le concept de l’espace-temps où tout va toujours à la vitesse de la lumière tout le temps. C’est-à-dire que vous, qui êtes devant votre écran en train de lire cet article, vous vous déplacez à la vitesse de la lumière dans l’espace-temps. À chaque seconde, dans l’espace-temps, vous parcourez 300 000 km. En d’autre mot, la monnaie d’échange entre le temps et l’espace, c’est la vitesse de la lumière. Vous allez donc vers le futur à la vitesse de la lumière. Mais quelqu’un qui se déplacerait, dans l’espace, par rapport à vous à une très grande vitesse, irait toujours à la vitesse de la lumière dans l’espace-temps. Simplement le fait que ce quelqu’un soit en déplacement par rapport à vous, dans l’espace, diminuerait la vitesse avec laquelle il va vers le futur. Autrement dit, se déplacer dans l’espace, c’est ralentir la vitesse à laquelle on va vers le futur.

Pour ceux qui veulent comprendre la relativité restreinte et la raison pour laquelle se déplacer dans l’espace, c’est ralentir la vitesse à laquelle on va vers le futur, je vous recommande la conférence sur les notions de base de la relativité générale et la relativité restreinte donnée par Roland Lehoucq, astrophysicien au CEA (Commissariat à l’Énergie Atomique et aux énergies alternatives) conférence du 29 mars 2017. C’est vraiment très bien expliqué pour que tout le monde comprenne. Vous comprendrez entre-autres les changements de référentiels de l’espace-temps par les transformations de Lorentz sous forme de graphiques et comment on doit gérer le synchronisme des horloges atomiques qui sont à bord des satellites GPS.

Fig. 1 : La conférence de Roland Lehoucq, astrophysicien au CEA (Commissariat à l’Énergie Atomique et aux énergies alternatives), sur la relativité générale et la relativité restreinte le 27 mars 2017. Source Youtube.

Remarque : Les paragraphes qui suivent sur la description des particules élémentaires qui constituent l’atome et sur la description des forces d’interactions entre ces particules ont été inspirés de deux conférences d’Étienne Klein, physicien et philosophe des sciences dirigeant le laboratoire de recherche sur les sciences de la matière et consacrant sa vie à la vulgarisation autour des questions soulevées par la physique contemporaine, notamment par la physique quantique et la physique des particules. Certaines parties de ces paragraphes sont des retranscriptions intégrales d’extraits des conférences d’Étienne Klein car ce physicien maîtrise particulièrement bien l’art de la vulgarisation en expliquant des concepts abstraits et complexes avec des mots simples et compréhensibles par tous.

Fig. 2 : La conférence d’Étienne Klein, physicien et philosophe des sciences, directeur du laboratoire de recherche sur les sciences de la matière ; La structure fondamentale de la matière ; le 24 mai 2018. Source Youtube.

Fig. 3 : La conférence d’Étienne Klein, physicien et philosophe des sciences, directeur du laboratoire de recherche sur les sciences de la matière ; Qu’est-ce que la masse et le boson de Higgs ? ; le 27 mars 2014. Source Youtube.

Façon dont on comprend les interactions fondamentales en physique ; les forces :

En physique classique, c’est très simple ; on pense à la force gravitationnelle ou à la force électromagnétique. Un objet matériel, électrique ou pas, crée un champ. Si c’est un objet massif, il crée un champ gravitationnel, si c’est une charge électrique, elle crée un champ électrique qui est partout présent dans l’espace et que l’on peut calculer (avec les équations de Maxwell). Si on place une particule dans ce champ, une particule chargée ou une particule qui a une masse, elle va subir une force à l’endroit où elle se trouve et qui est proportionnelle à l’amplitude du champ. Une masse crée donc un champ de gravitation et ce champ de gravitation engendre une force de gravitation pour les objets qui s’y trouvent. Une charge électrique crée un champ électrique qui va exercer une force sur les charges électriques qui se trouveront dans ce champ. En physique classique, une force se transmet par l’entremise d’un champ.

En physique quantique, les choses en vont tout autrement. Il est relativement difficile de se représenter les phénomènes qui se passent en physique quantique par des images ou par une représentation réelle. En effet, tout se calcule par des mathématiques relativement complexes et abstraites. Tout ce que l’on peut faire, c’est prendre des métaphores, dire ce qu’il faut en retenir et dire ce qu’il faut abandonner pour ne pas se laisser tromper.

Voici quelques exemples de concepts et outils mathématiques abstraits de la physique quantique. Ces mathématiques parlent de fonction d’état dans un espace de Hilbert à quatre dimensions, de théorie de jauges, de Lagrangien, de symétrie et de brisure de symétrie, de symétrie globale, de symétrie locale, de symétrie de jauge, de champ de jauge et d’espaces fibrés, de facteur d’échelle par un nombre complexe de module unitaire, de rotation vectorielles du plan, de rotation de l’espace à trois dimensions, de quadrivecteurs, de groupe abélien et non-abélien, de chromodynamique quantique, etc. Bref, beaucoup de mots barbares qui sortent du cadre de cet article. Toutefois, on donnera plus loin une brève description des symétries de jauge.

Il est toutefois remarquable que les mathématiques de la physique quantique ont pu prédire des phénomènes qui se sont toujours vérifiés par les expérimentations, entre autres dans les accélérateurs de particules. Une des dernières découvertes est le boson de Higgs-Englert prédit en 1964 et découvert en 2012. Nous en reparlerons vers la fin de cet article.

Pour se représenter les forces qui existent entre les particules, on va prendre une métaphore qui matérialise les interactions qui agissent entre les particules. En physique quantique, une interaction entre deux objets est aussi une affaire d’objets. C’est-à-dire que quand deux particules interagissent, il faut imaginer qu’elles échangent d’autres particules qui sont caractéristiques de l’interaction qu’elles subissent.

Par analogie, imaginons deux barques qui circulent sur un lac où il n’y a pas le moindre courant d’eau ni de vent ni de vague à la surface. Les deux barques sont en mouvement sur des trajectoires qui se croisent et les barques sont sur le point de rentrer en collision au croisement de leurs trajectoires respectives. Les deux passagers qui se trouvent à bord des barques (un passager par barque) ne disposent d’aucun moyen de diriger celles-ci ni de modifier leurs trajectoires : pas de gouvernail, pas de pagaille, pas de perche, pas de rame, pas de moteur, pas de voile. Si les passagers ne font rien, c’est la collision assurée entre les deux barques. Imaginons qu’un des deux passagers possède un ballon de football qui a une certaine masse et que les deux passagers commencent à se faire des passes avec le ballon en se le renvoyant tour à tour l’un à l’autre. Grâce à cette succession de passes qu’ils se font, par le principe de l’action et de la réaction il y a un échange d’une quantité de mouvement (p = mv), et cela va créer une force répulsive qui fait que les deux barques vont finir par s’éloigner l’une de l’autre. Cette analogie, certes critiquable, permet d’expliquer comment s’effectuent les interactions entre les particules. Tout se passe comme si les particules s’échangeaient des ballons qui sont caractéristiques des interactions qu’elles subissent. Il est à remarquer que plus le ballon est lourd, et plus la portée de l’interaction est proche : il est difficile de lancer au loin un ballon très lourd. Les interactions entre particules au moyen de particules d’interaction lourdes sont presque des interactions de contact. Plus le ballon est léger et plus il est facile de le lancer de très loin. À la limite, l’interaction entre particules qui s’effectuent par des particules d’interaction de masse nulle a une portée infinie.

Les interactions fondamentales entres les particules de l’atome :

Il y a quatre types de forces dont trois qui sont fondamentales et qui caractérisent les interactions qui existent entre les particules :

1. La gravitation qui est une force dont l’intensité est tellement faible au niveau des particules qu’elle est presque négligeable en physique quantique.
2. L’interaction électromagnétique, dans le cadre de la physique quantique, est médiatisée par le quantum de lumière qui est le photon dont la masse est nulle et dont la portée est infinie. Par exemple, quand deux électrons se repoussent par la force électrique, en fait ils échangent des photons en permanence ; ces photons, on les appelle des photons virtuels.
3. L’interaction nucléaire faible agit entre les particules du noyau de l’atome (protons et neutrons) qui est médiatisée par trois sortes de particules appelées les bosons intermédiaires W⁺ avec une charge positive, W^– avec une charge négative (« W » comme Weak = faible en anglais) et Z₀ de charge nulle et dont les masses sont élevées (environ 90 fois celle d’un proton). Il s’agit d’une interaction presque de contact ; en effet, les protons et les neutrons qui se situent dans le noyau de l’atome sont proches les uns des autres. C’est par exemple ce type d’interaction qui est responsable de la désintégration d’un neutron en un proton + un électron + un neutrino. C’est le cas dans la désintégration du potassium d’isotope 40 (K⁴⁰) présent dans notre corps humain en du calcium d’isotope 40 (Ca⁴⁰) où un proton se transforme en neutron avec l’émission d’un électron et d’un neutrino pour respecter le principe de conservation de l’énergie.  Cette émission est appelée la radioactivité β (bêta) qui, dans notre corps humain, est une radioactivité naturelle qui se déroule au rythme de 4000 coups par seconde. Le type d’interaction nucléaire faible est aussi responsable du fonctionnement du soleil : le soleil brûle son hydrogène pour le transformer en hélium (nucléosynthèse) à un rythme très lent qui fait que la durée de vie de notre étoile est de plusieurs milliards d’années.
4. L’interaction nucléaire forte agit entre les particules qui composent les protons et les neutrons, c’est-à-dire les quarks ; les interactions entre les quarks sont médiatisées par les gluons qui ont une masse nulle.

Il y a 6 types de quarks : up, down, charm, strange, top et bottom. Les quarks ont une charge de couleur : rouge r, vert v et bleu b (chromodynamique quantique). Les quarks peuvent changer de couleur en échangeant des gluons. Les quarks peuvent parfois se présenter sous la forme de paires quark et antiquark : 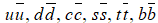où l’antiquark est l’antiparticule du quark. Un antiquark a une charge électrique opposée à celle du quark et a une anti-couleur : anti-rouge, anti-vert et anti-bleu. Les quarks ont la caractéristique de ne se présenter jamais seuls (phénomène de confinement) et sont toujours assemblés de telle sorte que la somme de leur charge soit un multiple entier d’une charge élémentaire (par exemple 0 pour le neutron et 1 pour le proton) et sont assemblés de telle sorte que la « somme » de leur charge de couleur soit blanche (selon la règle de la synthèse additive des couleurs ; il s’agit de la règle de neutralité où 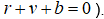Un assemblage de trois quarks de chacune des trois couleurs forme un baryon. Un assemblage d’un quark et d’un antiquark de charge de couleurs complémentaires qui s’annulent forme un méson. Les baryons et les mésons sont donc des assemblages de quarks et font partie de la famille des hadrons.

Un proton est constitué de trois quarks : deux quarks up et un quark down. Un neutron est constitué aussi de trois quarks : deux quarks down et un quark up.

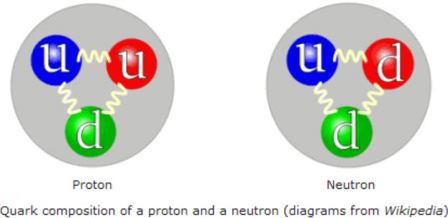
Fig. 4 : Représentation des assemblages de quarks dont la somme des charges de couleurs est blanche selon la synthèse additive des couleurs. Ces groupes de trois quarks sont des baryons faisant partie de la famille des hadrons. Il s’agit ici d’un proton et d’un neutron. Source : graphisme Wikipédia.

Il y a 8 types de gluons ; chaque gluon possède une charge de couleur : rouge r , vert v et bleu b (chromodynamique quantique) et une anti-charge d’anti-couleur :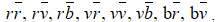
Le « 9^ème gluon 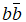n’est pas indépendant des autres et n’existe donc pas car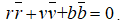

L’interaction nucléaire forte possède une propriété tout-à-fait étonnante que l’on appelle la liberté asymptotique, ce qui signifie en des mots simples que, contrairement à l’interaction électromagnétique et l’interaction nucléaire faible, l’interaction nucléaire forte exerce une force d’attraction d’autant plus grande que la distance entre les quarks augmente : on la compare à la force de rappel exercée par un ressort qui est tendu. C’est ainsi que l’on représente graphiquement les gluons par des petits ressorts en forme de boudins qui relient les quarks. Si l’on exerce une force suffisante pour extraire un quark à un nucléon, le « ressort finit par casser ». Dans ce cas, l’énergie dépensée pour tirer sur le ressort se matérialise sous la forme d’une paire de quark et d’antiquark. Le quark qui est créé reste dans le nucléon et l’antiquark accompagne le quark que l’on a arraché (la paire constitue un méson). Dans cette opération, la règle de neutralité est respectée : r+v+b=0. À l’opposé, lorsque les quarks sont très proches les uns des autres, la force de rappel disparaît presque complètement, d’où l’on évoque la notion de liberté asymptotique. De ce fait, les quarks sont confinés par l’interaction nucléaire forte au sein des nucléons mais ils sont quasiment libres de leurs mouvements à l’intérieur de ceux-ci.

Il existe en fait une infinité de gluons car ceux-ci peuvent être représentés par un état combiné, par exemple sous la forme de la combinaison linéaire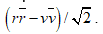

L’interaction nucléaire forte est ainsi relativement complexe et la chromodynamique quantique est la plus complexe des théories de jauge à ce jour (voir explications plus loin avec les groupes de symétrie). Le succès de la chromodynamique quantique démontre de manière éclatante la pertinence de la démarche.

Distinctions entre les particules élémentaires de l’atome :

Au niveau des particules élémentaires, il y a des particules qui ne subissent pas l’interaction nucléaire forte car elles n’y sont pas sensibles. Ces particules, on les appelle des leptons (du grec λεπτος qui signifie « léger ») et forment une sous-famille des fermions. Il y a 6 sortes de leptons de trois « saveurs » différentes : l’électron e^–, le muon μ^– qui est une sorte d’électron « lourd » et le tau (tauon) τ^– qui sont des particules avec une charge électrique et une masse non nulle. Il y a d’autres particules qui y sont associées : le neutrino électronique, le neutrino muonique et le neutrino tauique sans charge électrique et de masse non nulle. À ces 6 particules sont associées des antiparticules de charge opposée c’est-à-dire le positron e⁺, l’anti-muon μ⁺ et l’anti-tau τ⁺ ainsi que les 3 antiparticules associées : les anti-neutrinos.

Il y a les particules élémentaires qui subissent l’interaction nucléaire faible, les hadrons qui sont au nombre d’une centaine de types parmi lesquels on distingue deux familles : les hadrons constitués de trois quarks (baryons) et les hadrons constitués d’une paire de quark et antiquark (mésons). En ce qui concerne l’interaction nucléaire forte, il faut se représenter que les quarks interagissent en s’échangeant des gluons.

Description des interactions entre les particules élémentaires de l’atome (groupes de symétrie et théories de jauge) :

Après la 2^ème guerre mondiale, il y a des physiciens théoriciens qui ont eu des idées assez incroyables. Ils ont eu l’idée d’associer chacune des interactions à ce qu’on appelle un groupe de symétrie. Qu’est-ce qu’une symétrie ? Dans la vie courante, une symétrie est une opération qui ne change pas la forme d’un objet, qui le laisse invariant. Par exemple, si on prend une sphère et que l’on fait tourner celle-ci par n’importe quel axe qui la traverse et passe par son centre, cela ne change pas sa forme et cela ne change pas non plus sa position. Cette rotation laisse la sphère invariante. Les physiciens ont identifié des groupes de symétrie qui laissent la structure des interactions invariante. Par exemple, le groupe de symétrie associé à l’électromagnétisme, c’est l’ensemble des nombres complexes dont le module est égal à 1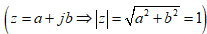et qui s’écrivent en notation d’Euler sous la forme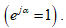

Il se trouve que, dans le cadre de la mécanique quantique, si l’on fait l’hypothèse que le groupe de symétrie de l’électromagnétisme, c’est l’ensemble des nombres qui s’écrivent sous cette forme, alors le formalisme est tel qu’il permet de calculer toutes les propriétés de l’interaction. L’identification du groupe détermine l’interaction. L’identification de la symétrie de l’interaction détermine toutes ses propriétés. En ce qui concerne l’électromagnétisme, le groupe de symétrie est appelé U(1).

La chose incroyable, c’est que très peu de temps après les physiciens théoriciens ont pu faire le même type d’opération pour l’interaction nucléaire faible et pour l’interaction nucléaire forte : on a trouvé un groupe de symétrie pour l’interaction faible qui s’appelle SU(2) (matrices 2 x 2 spéciales unitaires) et on a trouvé un groupe de symétrie pour l’interaction forte qui s’appelle SU(3) (matrices 3 x 3 spéciales unitaires). Ce qui est extraordinaire c’est que le seul fait de fixer ces groupes, de les identifier, détermine complètement la structure des interactions.

Les groupes de symétrie portent le nom de symétrie de jauge. Elle correspond à l’invariance d’un système physique sous l’action locale d’un groupe de symétrie appelé groupe de jauge dans les théories de jauge. Cela signifie qu’il est possible d’effectuer une transformation donnée à un élément du groupe de symétrie de façon indépendante en chaque point de l’espace-temps sans affecter le résultat des observations. La transformation s’effectue à l’aide d’un outil mathématique qui est le lagrangien. En quelques mots, le lagrangien (découvert par le mathématicien Joseph-Louis Lagrange en 1788) est une fonction mathématique qui permet d’écrire de manière concise les équations du mouvement d’un système faisant intervenir la position, la vitesse et l’accélération d’un objet en exprimant une relation où interviennent l’énergie cinétique, la quantité de mouvement et l’énergie potentielle de cet objet dans le cadre de la mécanique classique. Le formalisme du lagrangien est aussi applicable dans la théorie des champs physiques et dans les théories de jauge de la physique quantique.

Après la 2^ème guerre mondiale, on construit des nouveaux accélérateurs de particules, on fait des collisions, on a beaucoup de données expérimentales, on obtient un nombre de données qui augmente très rapidement au cours du temps. Il se trouve que la théorie que l’on construit ainsi qui s’appelle le modèle standard de la physique des particules est une théorie qui rend compte des événements que l’on peut détecter dans les détecteurs de particules. Autrement dit, on a un modèle, une théorie, qui permet d’expliquer les choses de façon élégante parce que ces trois interactions qui, d’un point de vue phénoménologique sont complètement différentes, en fait sont décrites de la même façon par ce qu’on appelle les théories de jauge.  Un groupe de symétrie détermine l’interaction, ce n’est pas le même groupe pour les trois interactions (électromagnétisme, force faible et force forte) mais le formalisme mathématique est le même pour les trois groupes. Cela donne un côté très unificateur qui est toujours apprécié parce qu’il est synonyme d’une forme d’élégance dans le formalisme mathématique. Tout va bien, puisqu’on rencontre des résultats, on a une sorte de théorie physique (théorie de jauge) qui décrit parfaitement le monde de l’infiniment petit.

Le problème, on le constate au début des années 60, est que si l’on suppose que les équations de ce modèle sont justes et si on regarde ce qu’elles impliquent – on fait une sorte d’expérience de pensée – qu’est-ce qui se passerait si les équations étaient vraiment justes ? On se rend compte que, si les équations sont vraiment justes, alors les masses de tous les ballons que les passagers se passent l’un à l’autre dans l’analogie avec les deux barques sur le lac, c’est-à-dire les particules qui médiatisent les interactions, leurs masses devraient être nulle. Autrement dit, toutes les interactions devraient avoir une portée infinie et devraient être médiatisées par des particules de masse nulle. Cela va même plus loin car il y a une sorte de phénomène de contagion : si les particules d’interaction ont des masses nulles, alors les particules qui subissent l’interaction devraient aussi avoir des masses nulles. Autrement dit, le modèle standard qui marche très bien prédit, si on le prend au sérieux, que les masses de toutes les particules élémentaires doivent être égales à zéro. Ce qui n’est pas ce que l’on constate : les bosons intermédiaires W⁺, W^– et Z₀ qui caractérisent l’interaction faible sont très lourds et les électrons ont une masse non nulle. Donc il y a une contradiction entre ce que l’on mesure et ce que dit ce modèle. Comment résoudre cette contradiction ?

Rappelez-vous de tout ce qui a été décrit ci-dessus à propos de la masse. L’idée que nous avons de la masse qui est intriquée avec la notion de quantité de matière est indéracinable dans notre cerveau. Quand on pense masse, on pense matière et quand on pense matière, on pense masse. C’est la découverte du boson de Higgs qui va défaire cette idée d’intrication entre matière et masse.

On commençait à comprendre, grâce à l’équation d’Einstein E = mc², que dans les atomes, il y a une énergie de masse, c’est-à-dire que l’énergie contenue dans les atomes font que ceux-ci ont une masse. Cela reste toujours vrai. La découverte du boson de Higgs va simplement élargir ce concept aux particules élémentaires qui, selon le modèle standard des particules sont toutes de masse nulle. Le boson de Higgs est une particule qui caractérise le champ scalaire de Higgs. Un champ scalaire est par exemple un champ de température : il y a telle température à tel endroit de l’espace. Dans cet exemple, le champ scalaire de température indique les températures qu’il y a en tous points de l’espace. Ainsi, depuis la découverte du boson de Higgs, on a pu résoudre la contradiction de la masse nulle des particules selon le modèle standard. Les particules élémentaires de l’atome interagissent avec le vide qui n’est pas vide car il est rempli par le champ de Higgs qui est présent partout dans l’espace. Le boson de Higgs est le quantum du champ scalaire de Higgs. Par comparaison, le photon est le quantum du champ électromagnétique. Les particules élémentaires acquièrent de la masse à cause de leur interaction (on parlera de couplage) avec le champ scalaire de Higgs. La masse des particules élémentaires n’est donc plus contenue dans ces particules élémentaires, cette masse devient une manifestation secondaire des particules élémentaires et cette manifestation de masse a lieu grâce au couplage que les particules élémentaires ont avec le champ de Higgs. Nous reviendrons plus loin au boson de Higgs.

Au secours ! Je ne comprends plus rien. E = mc², cela veut dire quoi ?

Nous sommes bien d’accord : la masse d’un sac de billes est égal à la somme des masses des billes qui le constituent plus la masse du sac. Si ce raisonnement est correct, il implique que la masse de notre corps qui est constitué de particules élémentaires qui sont des petites billes doit être égale à la somme des masses des particules qui le constitue. Or la vérité est tout autre : la somme des masses des particules qui nous constituent ne représente que quelques pourcents de la masse totale de notre corps. D’où vient la masse majoritaire de notre corps ?

En 1905, Einstein écrit : Le principe de la relativité associé à l’électromagnétisme impose que la masse d’un corps soit la mesure directe de l’énergie qu’il contient : E = mc². Comment Einstein démontre-t-il cette formule ? En considérant un métal que l’on chauffe (le filament d’une ampoule électrique à incandescence, par exemple) et qui rayonne donc de l’énergie sous forme de lumière visible ou invisible (par exemple du rayonnement infra-rouge). La lumière n’a pas de masse (les photons ont une masse nulle). Donc ce corps qui rayonne de la lumière perd de l’énergie (ΔE) puisque la lumière contient de l’énergie mais ce corps ne pourrait pas perdre de masse (Δm x c²) puisque la lumière n’a pas de masse. Comment un corps qui rayonne des objets qui n’ont pas de masse pourrait-il perdre de la masse ? Einstein conclu que si l’on en croit les principes de sa théorie, alors le corps, du seul fait qu’il perd de l’énergie perd également de la masse, et cette masse qu’il perd est donnée par la formule suivante :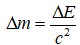 avec c qui est la vitesse de la lumière et qui vaut 10⁸ m/s.

Donc, même si le corps émet des objets qui ne sont pas massifs, il perd quand-même de la masse. Le génie d’Einstein le pousse à dire que cette formule qui fait intervenir la vitesse de la lumière doit demeurer vraie même si aucune lumière n’intervient dans le processus par lequel le corps en question perd de l’énergie. Autrement dit le statut de la vitesse de la lumière est changé. La vitesse de la lumière ne désigne plus seulement la vitesse de propagation d’un phénomène physique particulier qui est la lumière.

La vitesse de la lumière devient une constante universelle de la physique qui intervient dans tous les processus dans lesquels de l’énergie est mise en jeu même si aucune lumière n’intervient dans l’affaire.

Les implications de cette formule sont considérables. Par exemple, la formule implique que n’importe quel morceau de matière contient de l’énergie du seul fait qu’il est massif, même si le corps est immobile, au repos, il a une énergie mc² qu’on obtient en multipliant sa masse en kg par le carré de la vitesse de la lumière. Il y a d’autres implications : par exemple celle qui permet de répondre à la question posée. Les particules élémentaires qui nous constituent, par exemple les quarks, ces petites particules qui sont dans nos protons et nos neutrons, elles interagissent très fortement à des vitesses très grandes et cette énergie d’interaction correspond à une masse effective qui constitue l’essentiel de la masse de notre corps. Autrement dit la masse de notre corps doit beaucoup plus à la danse frénétique de nos particules élémentaires qu’à leur masse propre qui est très faible par rapport à la masse totale de notre corps.

Ensuite, il y a des phénomènes que l’on peut voir tous les jours en laboratoire, qui sont très étonnants, dont il n’existe aucune contrepartie dans la vie courante mais qui sont réglés par cette formule E = mc². Par exemple, si l’on prend deux protons de haute énergie, comme on le fait au CERN avec le grand collisionneur de particules (LHC), si ces deux protons entrent en collision à des énergies très grandes, on s’aperçoit que la collision va engendrer des centaines, voire des milliers de nouvelles particules et la somme des masses de toutes les particules ainsi créées est bien plus grande que la masse des deux particules incidentes (les deux protons de très grande énergie qui sont rentrés en collision). Que s’est-il s’est passé ? Il s’est passé que la vitesse des protons, leur énergie cinétique, par la formule E = mc² s’est transformée en masse, c’est-à-dire en nouvelles particules. Et là, il y a un phénomène très étrange qui est que la propriété d’un objet, en l’occurrence la vitesse des protons s’est matérialisée en d’autres objets.

D’autres exemples qui illustrent la formule E = mc² pour mieux comprendre :

Dans les exemples qui vont suivre, on va rentrer de plus en plus profondément dans la matière en partant d’un atome d’hydrogène, ensuite on ira au niveau du noyau d’un atome d’hélium et enfin on va rentrer à l’intérieur d’un proton et d’un neutron où se situent les quarks et les gluons. On constatera que l’essentiel de la masse de notre corps est contenue dans l’énergie colossale qui est contenue dans les interactions qui existent entre les quarks et qui est médiatisée par les gluons. Comme nous l’écrivions ci-dessus : la masse de notre corps trouve son origine dans l’énergie qui existe grâce à la danse frénétique de nos particules élémentaires.

Dans ce qui suit, nous reprendrons quelques éléments de l’exposé pédagogique de David Louapre, docteur en physique et connu pour son travail de vulgarisation scientifique sur sa chaîne Youtube « Sciences étonnantes ».

La masse d’un proton est de 1,673.10^-27 [kg].  La masse d’un électron est de 9,109.10^-31 [kg]. On devrait s’attendre à ce que la masse d’un atome d’hydrogène constitué d’un proton et d’un électron soit la somme des masses de ces deux particules ; eh bien non car quand on associe un proton et un électron, on diminue l’énergie potentielle du système. C’est d’ailleurs la raison pour laquelle le proton et l’électron s’associe pour créer une liaison : ils s’attirent parce qu’ils préfèrent être dans un état d’énergie potentielle la plus basse.

On peut en tirer comme leçon que l’état le plus stable de la matière correspond à un abaissement du niveau d’énergie de la matière.

La formation d’un atome d’hydrogène libère donc une certaine quantité d’énergie ΔE. Comme cet atome, en se formant, a perdu de l’énergie, il a aussi perdu de la masse :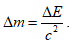 À cause de cette perte d’énergie, l’atome d’hydrogène a une masse inférieure à celle de la somme de ses constituants.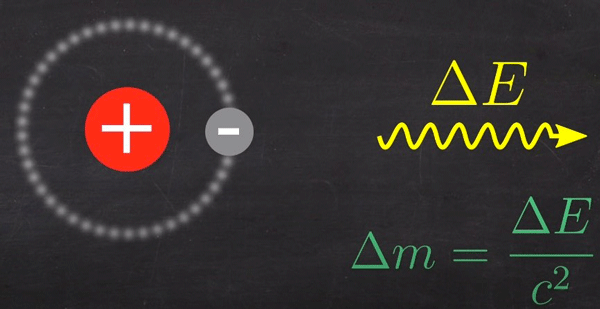

Fig. 5 : Libération d’énergie et perte de masse d’un atome d’hydrogène lors de sa formation. Source : graphisme de David Louapre © Science étonnante ; Youtube.

Une manière équivalente de le dire est que l’énergie libérée par l’atome d’hydrogène lors de sa formation c’est aussi celle qui est nécessaire pour le casser ; c’est ce qu’on appelle l’énergie d’ionisation. Quand on sépare les constituants d’un atome d’hydrogène, on lui apporte de l’énergie et on augmente donc la somme des masses des constituants de cette même quantité. Dans le cas de la formation ou la séparation d’un atome d’hydrogène la variation de masse est très faible et vaut à peu près un milliardième de la masse de cet atome.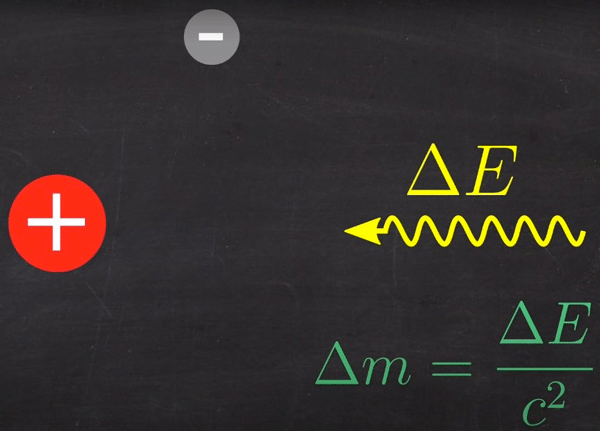
Fig. 6 : Énergie nécessaire et gain de masse des constituants séparés d’un atome d’hydrogène lors de son ionisation. Source : graphisme de David Louapre © Science étonnante ; Youtube.

Voyons maintenant un exemple où la variation de masse est beaucoup plus significative, ce qui est le cas dans le noyau d’un atome d’hélium qui est constitué de deux protons et de deux neutrons. La masse d’un proton est 1.673.10^-27 [kg] et celle d’un neutron est 1.675.10^-27 [kg].

Si l’on additionne séparément les masses de deux protons et de deux neutrons, on obtient une masse de 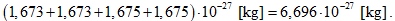Or la masse d’un noyau d’hélium est de 6,646.10^-27 [kg] . La masse d’un noyau d’hélium est donc inférieure à la somme des masses de ses constituants. Cette perte de masse s’accompagne d’un rayonnement d’énergie. La constitution d’un noyau d’hélium s’effectue par fusion nucléaire ; c’est ce qui se passe dans la réaction en chaine de fusion nucléaire dans le soleil où des protons d’atome d’hydrogène et des neutrons fusionnent pour former des atomes d’hélium. Le soleil rayonne beaucoup d’énergie par ce processus et il ne cesse de perdre de la masse au cours du temps.
Voici ci-dessous le détail de cette réaction en chaîne où l’on peut observer l’émission de rayonnement gamma et l’éjection de positrons et de neutrinos.

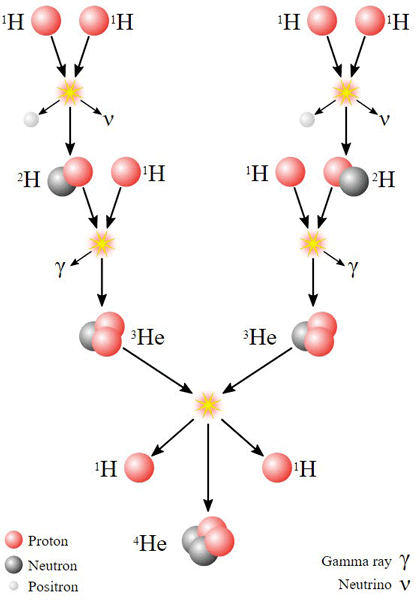
Fig. 7 : Réaction en chaîne de fusion nucléaire dans le soleil où les atomes d’hydrogène forment des atomes d’hélium avec un rayonnement d’énergie. Source : Wikimedia commons.

La perte de masse lors de la constitution d’un noyau d’hélium est de l’ordre de 1 % de la somme des masses de ses constituants. Cela peut paraître peu, mais en fait c’est énorme et cela permet au soleil de nous envoyer de la lumière et aux étoiles de briller. Cela veut dire aussi que les 99 % restant de la masse représentent une quantité d’énergie fabuleuse.

Alors, où se trouve donc les 99 % de la masse qui reste et ou se cache l’énergie qu’elle contient ? Pour cela, il va falloir rentrer dans les protons et les neutrons pour s’intéresser aux quarks. Comme on a fait pour les atomes et les noyaux, on peut regarder comment la masse d’un proton ou d’un neutron est reliée à la masse des quarks qui le constituent.

Les masses seront exprimées en yocto gramme : 1 yg = 10^-24 g. La masse d’un proton est de 1,673 yg et celle d’un neutron est de 1,675 yg. Un proton est constitué de deux quarks up et d’un quark down ; un neutron est constitué d’un quark up et de deux quarks down.  La masse d’un quark up est de 0,004 yg et celle d’un quark down est de 0,009 yg. Les quarks interagissent par des gluons et ces derniers ont une masse nulle.

On constate rapidement que la somme des masses des quarks est de loin très inférieure à la masse d’un proton ou d’un neutron. Alors, où se trouve le reste de la masse ?

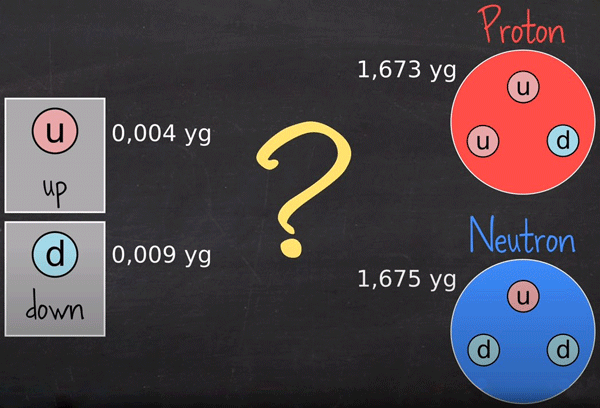
Fig. 8 : Masse des quarks up et down et masse du proton et du neutron. Source : graphisme de David Louapre © Science étonnante ; Youtube.

On sait que la masse, c’est du contenu en énergie. Ce qui explique la masse d’un proton et d’un neutron, c’est à 99 % de l’énergie d’interaction entre les quarks. Au sein des protons et des neutrons les quarks sont « reliés » par ce qu’on appelle l’interaction forte (force nucléaire forte). Les quarks interagissent et s’attirent en échangeant d’autres particules que l’on appelle des gluons. On représente souvent les gluons comme des petits ressorts en forme de boudin qui relient les quarks. Cette représentation n’est pas innocente car plus on veut éloigner deux quarks l’un de l’autre, plus ils interagissent et plus la « force de rappel » est grande (plus ils s’attirent). L’attraction entre deux quarks ne devient faible que lorsqu’on les rapproche fortement (on parle de liberté asymptotique).

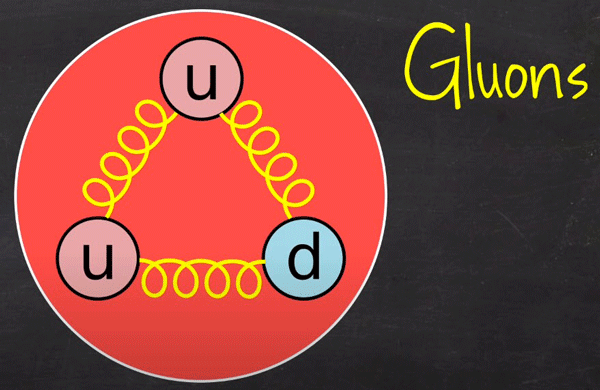
Fig. 9 : Représentation des gluons qui sont les particules d’interaction entre les quarks. Source : graphisme de David Louapre © Science étonnante ; Youtube.

Comme l’existence de cette attraction et de cette interaction entre les quarks provoquent leurs mouvements, ils déploient à la fois une énergie cinétique du fait de leur vitesse et une énergie potentielle d’interaction. Ces deux formes d’énergies constituent l’énergie interne globale d’un proton ou d’un neutron et cette énergie interne contribue à 99 % de leurs masses respectives. Ainsi, pour les protons et les neutrons qui représentent l’immense majorité de la matière de notre corps, l’origine de la masse ne vient pas de ses constituants, les quarks, mais de leur énergie : leur énergie cinétique et leur énergie d’interaction.
Dans la réalité, la situation est un peu plus complexe. Quand on essaye d’éloigner deux quarks, la force entre les deux augmente. Cela a une conséquence un peu contre-intuitive : il n’est pas possible d’observer un quark tout seul ou isolé ; c’est ce qu’on appelle le confinement des quarks. Si on essaye quand-même de tirer sur cette sorte de ressort (le gluon), au bout d’un moment il se passe un phénomène étonnant : le ressort, c’est-à-dire le gluon se désintègre et l’énergie qu’il contenait se transforme en une paire de quarks et une parie de quark et d’antiquark qui peuvent d’ailleurs être d’un type différents de up et down. Inversement, des paires de quarks et d’antiquarks peuvent fusionner et disparaître en redonnant de l’énergie au gluon.

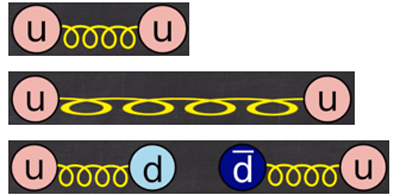
Fig. 10 : Formation de paires de quarks et d’antiquarks à partir d’une parie de quarks. Source : graphisme de David Louapre © Science étonnante ; Youtube.

Il est à remarquer que dans l’interaction forte, les gluons sont de masse nulle, ils ont donc une portée infinie d’interaction. Mais la portée effective de l’interaction est très petite tout simplement parce que les quarks ne peuvent pas exister tout seul. Ils sont forcément dans des paquets : soit des paquets de trois quarks comme dans le proton et le neutron, soit des paquets formés par un quark et un antiquark comme dans les mésons. Les quarks ne sont donc jamais tout seul : ils sont confinés à l’intérieur des hadrons de sorte que la portée effective de l’interaction forte est très petite et a la taille des protons et des neutrons. Pour rappel, les hadrons sont des protons, des neutrons ou des mésons. Quand on crée des quarks lors de collisions de particules, on peut faire sortir un quark de la collision, mais très vite il va faire sortir du vide des paires de quarks et d’antiquarks pour faire fabriquer des particules composites. Cela va provoquer ce que l’on appelle des jets dans les détecteurs d’un collisionneur de particules : on verra des quarks habillés d’autres quarks pour former des particules composites. Dans le jargon de la physique quantique, on dit que les quarks s’habillent pour sortir ; ils s’habillent d’autres quarks ou d’antiquarks.

À l’intérieur d’un proton ou d’un neutron, la cadence de création et de disparition de paires de quarks se produit à un rythme effréné. Une image correcte de leur structure interne n’est pas celle de trois quarks reliés par des gluons, mais plutôt d’une mer de quarks, d’antiquarks et de gluons qui évoluent sans cesse avec comme particularité qu’il y a en final trois quarks de plus qu’il y a d’antiquarks : deux up et un down pour un proton et un up et deux down pour un neutron.  Les paires de quarks et d’antiquarks peuvent être vues comme des particules virtuelles. De ce point de vue-là, une manière un peu plus correcte de voir ces 99 % d’énergie interne, c’est de voir l’énergie de cette mer de quarks qui dansent à un rythme frénétique et où les paires de quarks et d’antiquarks se font et se défont.

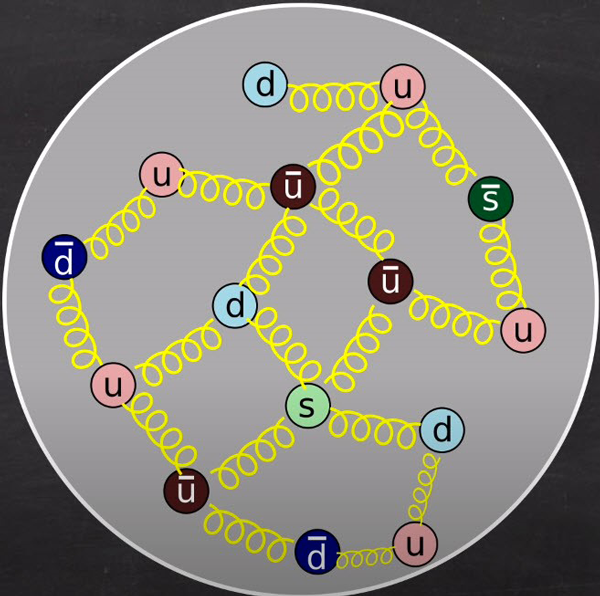
Fig. 11 : Structure interne d’un proton où les paires de quarks et d’antiquarks se font et se défont à un rythme effréné dans une mer de quarks et d’antiquarks.  Source : graphisme de David Louapre © Science étonnante ; Youtube.

À ce stade de notre voyage au plus profond de l’atome, vous remarquerez qu’on a déjà expliqué 99 % de la masse de notre corps, juste avec de l’énergie interne : l’énergie d’interaction des quarks. Depuis le début, on comprend que la nature de la masse c’est de l’énergie interne grâce à l’équation d’Einstein E = mc². Cela fonctionne bien car on a regardé des systèmes qui sont composites, c’est-à-dire faits de plusieurs constituants : un atome, un noyau, un proton. Mais un quark, jusqu’à présent, c’est une particule élémentaire qui n’est composée de rien d’autre que d’elle-même. Alors, même si la masse des quarks ne compte que pour 1 %, comment explique-t-on cette masse-là ? C’est ici qu’intervient le boson de Higgs, ou plutôt le champ scalaire de Higgs.

Le boson de Higgs et le champ scalaire de Higgs :

Le boson de Higgs est une particule élémentaire qui a été postulée par François Englert, Robert Brout et Peter Higgs en 1964 et découverte au LHC du CERN à Genève en 2012.  Cette particule permet d’expliquer pourquoi certaines particules élémentaires ont une masse (bosons intermédiaires W⁺, W^–, Z₀, électron, muon, neutrino, quarks, etc.) et d’autres n’en n’ont pas (photon, gluon).

Le photon est le quantum du champ électromagnétique. Le champ électromagnétique peut être nul lorsqu’il n’y a pas de source électromagnétique. Le boson de Higgs est le quantum du champ de Higgs. Le champ de Higgs est constant et n’est jamais nul ; ce champ scalaire remplit en permanence l’espace vide. L’espace vide n’est dès lors pas vide puisqu’il contient le champ de Higgs.  Les particules élémentaires interagissent avec le vide qui n’est pas vide, c’est-à-dire avec le champ de Higgs ; on parle de couplage de la particule élémentaire avec le champ de Higgs.  Cette interaction a pour conséquence que les particules élémentaires acquièrent une masse.

Pour comprendre ce phénomène en des mots simples, on peut utiliser la « métaphore du cocktail » qui a été décrite par le physicien David J. Miller, spécialiste des particules élémentaires qui a comparé le boson et le champ de Higgs à un cocktail réunissant les membres d’un parti politique. Le champ de Higgs est comparé au groupe des personnes qui, au départ, remplissent un salon de manière uniforme. Lorsqu’une personnalité politique très connue entre dans le salon, elle attire les militants autour d’elle, ce qui lui donne une « masse » importante. Cet attroupement correspond au mécanisme de Higgs, et c’est lui qui attribue une masse aux particules.

Ce n’est pas le boson qui donne directement une masse aux particules : le boson est une manifestation du champ de Higgs et du mécanisme de Higgs qui, lui, donne sa masse aux particules. Ceci est comparable, dans cette métaphore, au phénomène suivant : une personne extérieure, depuis le couloir, répand une rumeur aux personnes situées près de la porte. Un attroupement de militants se forme de la même manière et se répand, comme une vague, à travers la pièce pour transmettre l’information : cet attroupement correspond au boson de Higgs. L’observation du boson de Higgs serait donc un indice très fort de l’existence du mécanisme de Higgs.

Seulement 1 % de la masse de la matière usuelle peut être considérée comme causée par le boson de Higgs. En effet, la matière usuelle est faite d’atomes, eux-mêmes composés d’électrons et de nucléons (protons et neutrons). Or la masse des électrons est très faible, et 99 % de la masse des nucléons vient de l’énergie de liaison (par la force forte) entre quarks, eux-mêmes également très légers. Ces 99 % de la masse s’expliquent par la formule d’Einstein E = mc².

Dans les paragraphes qui suivent, nous allons reprendre les explications d’Étienne Klein dans sa conférence sur la structure fondamentale de la matière pour mieux comprendre ce mécanisme de Higgs.

La masse des particules élémentaires ne vient pas de leur matière :

Grâce au boson et au champ de Higgs, on va comprendre que la masse des particules élémentaires n’est pas une notion primitive qu’elles acquièrent du seul fait qu’elles sont des particules de matière, on va comprendre que la masse des particules élémentaires est une propriété secondaire qu’elles acquièrent du fait de leur interaction avec le vide qui n’est pas vide. Comment en est-on arrivé là ?

Il est apparu une contradiction entre ce qu’implique le modèle standard de la physique des particules – toutes les particules élémentaires doivent avoir une masse nulle – et puis le fait de constater que ce n’est pas vrai : elles ont une masse non nulle en général. Dès lors que dans les années 60, il y a une contradiction entre ce que prévoit le modèle standard et ce que donnent les mesures, les physiciens se disent qu’il y a une contradiction entre les faits et la théorie ; donc la théorie est fausse.  En général, c’est comme cela que l’on raisonne : « la théorie est fausse ». On cherche alors d’autres modèles, on met au point d’autres scénarios pour essayer d’expliquer les interactions telles qu’on les observe à partir d’autres concepts que ceux qui sont utilisés dans le modèle standard.

Prédiction et découverte de l’existence du boson de Higgs et du champ de Higgs :

À cette époque, en 1964, il y a trois jeunes physiciens qui ont de façon indépendante la même idée. Les deux premiers s’appellent François Englert, physicien belge qui travaille à Bruxelles et Robert Brout, physicien américain qui s’est fait naturalisé belge. Ensemble, ils écrivent un article en juin 1964. D’une façon indépendante, un physicien écossais, qui travaille tout seul et qui s’appelle Peter Higgs écrit un article en août 1964, quelques mois plus tard. Ces publications sont très courtes et sont à peine d’une page et demie avec des calculs sur la théorie des champs. L’idée est la même dans les deux articles.

L’idée est de dire, souvenons-nous de Galilée, le pari est d’expliquer le réel par l’impossible. C’est-à-dire que l’on peut expliquer ce que nous détectons, ce que nous mesurons, ce que nous observons grâce à des lois physiques qui contredisent l’observation directe.  Dans le cas de Galilée, quand il dit que tous les corps tombent à la même vitesse dans le vide, cette loi est vraie. Mais comment comprendre cette loi qui contredit l’observation, qu’elle puisse expliquer quand-même l’observation. Tout simplement en disant que quand on fait tomber des corps dans l’atmosphère, il y a la gravité qui les fait tomber tous à la même vitesse, mais il y a d’autres forces, la résistance de l’air, la poussée d’Archimède qui sont responsables, et seulement elles, du fait que les corps lourds ne tombent pas à la même vitesse que les corps légers. Donc la loi qui contredit l’observation oblige à une réinterprétation de l’observation.

Les physiciens Englert, Brout et Higgs vont reprendre ce type d’argument pour dire : peut-être que les équations du modèle standard qui disent que les particules élémentaires ont une masse nulle ont raison. Peut-être qu’il est vrai que les particules élémentaires ont une masse nulle et nous qui pensons que ce n’est pas le cas, peut-être nous nous trompons depuis très longtemps de l’interprétation de ce qu’il faut appeler la masse. Peut-être que la masse n’est pas une propriété intrinsèque des particules élémentaires, mais une propriété secondaire qui résulte de leur interaction avec le vide qui du coup n’est pas vide.

Ces physiciens vont supposer que le vide, ce qu’on appelle le vide ou l’espace vide contient, en tous points de l’espace, un champ. Un champ, un peu comme un champ de températures qui a une valeur en tous points, et le champ en question s’appelle le champ de Higgs. Ce champ est un champ scalaire, il est très simple, il est écrit par un nombre scalaire, comme un champ de température, il est partout présent dans l’espace.

Ces physiciens imaginent que les particules élémentaires de masse nulle, qui sont toutes de masse nulle comme le dit le modèle standard qui a raison, toutes les particules de masse nulle interagissent avec le champ plus ou moins fortement et c’est le couplage qu’elles ont avec le champ qui détermine leur masse. Nous voyons qu’elles ont une masse ou une inertie, on a l’impression que c’est elles-mêmes qui possèdent cette inertie et cette masse alors qu’elle résulte de leur interaction avec un champ. C’est comme si les particules se « frottaient » au vide.  Cette image est évidemment à prendre avec des pincettes parce que ce n’est pas un « frottement » mais c’est un couplage (il n’y a pas de dissipation). L’idée, c’est cela : ce qu’on appelle la masse c’est simplement une mesure du couplage que les particules ont avec le vide qui n’est pas vide puisqu’il contient un champ, c’est-à-dire le champ scalaire de Higgs.

Une métaphore pour se représenter le champ de Higgs :

Voici une autre métaphore du champ de Higgs ; cette métaphore, comme toutes les autres peuvent être critiquées. Imaginons que le champ de Higgs, ce soit un champ de neige d’épaisseur constante, l’amplitude est la même partout, il est homogène et que les cristaux de neige soient les bosons de Higgs. Imaginons que les particules élémentaires, sans masse, soient dotées de petits skis et qu’elles glissent sur le champ de neige. Si le fartage des skis est parfait (le fartage est l’application d’un enduit sur des skis, c’est-à-dire de la cire spéciale pour qu’ils glissent mieux sur la neige), cela veut dire qu’il n’y a aucune forme de couplage, aucune forme de « frottement » entre les skis et le champ de neige. Les particules vont glisser sans « frottement » et donc elles auront une vitesse qui est égale à la vitesse de la lumière. Nous qui voyons passer ces particules, nous dirons : « tiens, elles ont une masse nulle ». Si au contraire les particules ont des skis qui sont mal fartés, il va y avoir une forme de « frottement » et la vitesse des particules sera plus petite que la vitesse de la lumière et nous dirons : « tiens, elles ont une masse non nulle ». Autrement dit, cette hypothèse que font les trois physiciens Englert, Brout et Higgs, c’est l’idée que la masse est simplement une mesure de la mauvaise qualité du fartage des skis des particules. Moins les skis sont bien fartés, plus la masse, le couplage est important. On est invité ainsi à considérer que la masse des particules est le résultat d’une interaction.

Résolution du désaccord entre le modèle standard des particules et les observations :

Ici on a un cas intéressant puisqu’il mélange, à partir du désaccord entre la théorie et les mesures, une solution de type ontologique (c’est-à-dire ici au moyen de la prédiction d’une particule, le boson de Higgs qui doit exister pour expliquer les observations) et une solution de type législatif puisqu’on dit qu’il y a un champ qu’on n’a jamais vu et qui doit exister. Il y a non seulement quelque chose de plus qui existe dans l’univers (solution ontologique) et en plus il y a une nouvelle interaction entre les particules (solution législative avec une nouvelle loi physique), c’est-à-dire une interaction entre les particules et ce champ. Cette idée remonte aux années 60 et, en mécanique quantique, quand on a un champ comme celui de Higgs, il y a des règles, il y a des lois dans le formalisme qui implique que le champ doit être structuré en quanta. De la même façon que dans le champ électromagnétique il y a des photons, dans le champ de Higgs il y a des particules que l’on appelle le boson de Higgs qui sont les quanta de ce champ. Le nom « boson » vient d’un physicien indien qui s’appelait Bose et qui a introduit, dans les années 20, des particules obéissant à ce genre de statistiques.

Les essais qui ont permis la découverte du boson de Higgs :

La question est, dans les années 60 : est-ce que le champ de Higgs est une solution ? Est-ce que les articles publiés en 1964 par Englert, Brout et Higgs donnent la bonne explication du désaccord ou est-ce qu’il faut trouver autre chose ? Le problème, c’est que, une fois que l’on a fait l’hypothèse que le boson de Higgs existe, qu’on l’insère dans le modèle standard, ça marche, sauf que le modèle standard ne dit pas quelle doit être la masse de cette particule. Donc il faut faire des essais. Alors, comment peut-on détecter le boson de Higgs ?

On fait des collisions de particules à très haute énergie comme on le fait au CERN à Genève. On a essayé de le faire avec des électrons et des positrons dans une machine qui s’appelait le LEP (Large Electron Positron collider) qui a 27 km de circonférence dans un tunnel, les électrons tournaient dans un sens, les positrons (anti-particules) tournaient dans l’autre sens. On crée des collisions et, dans un tout petit volume de l’espace-temps, lors de ces collisions qui sont très brèves, on recrée les conditions physiques de l’univers primordial, c’est-à-dire les conditions de l’univers au moment de la naissance du Big Bang, donc très forte température, très forte densité. Le Big Bang est un modèle cosmologique utilisé par les scientifiques pour décrire l’origine et l’évolution de l’univers qui est en expansion depuis 13,8 milliards d’années. Comme les scientifiques pensent que les lois physiques n’ont pas changé au cours du temps, dès lors qu’on répète les conditions physiques du passé, on voit réapparaître les phénomènes physiques du passé. Donc, ces collisions, ce n’est pas des machines à remonter dans le temps, ce sont des opérations par lesquelles on recrée dans le présent des phénomènes physiques qui se sont déroulés dans le passé.

« Chauffer » le vide pour faire apparaître des particules virtuelles dans le monde réel :

Quand on fait de telles collisions, on « chauffe » le vide, c’est-à-dire le vide quantique.  Le vide quantique, c’est l’espace rempli de particules virtuelles qui sont « fatiguées » et qui n’ont pas assez d’énergie pour exister vraiment. En gros, elles ont une énergie inférieure à leur masse multipliée par le carré de la vitesse de la lumière : E < mc².  Elles ne sont pas vraiment réelles parce qu’elles n’ont pas leur énergie de masse. Quand on fait des collisions comme on vient de décrire, on transfère à ces particules « fatiguées » l’énergie qui leur manque de sorte qu’elles deviennent réelles : elles sortent du vide et on les détecte. Par des collisions, on peut recréer les conditions physiques de l’univers primordial et faire réapparaître des phénomènes qui n’existent plus aujourd’hui parce que l’univers est devenu trop froid et pas assez énergétique.

Du LEP au LHC à Genève :

Avec le LEP (Large Electron Positron collider), on n’avait pas assez d’énergie pour détecter le boson de Higgs dont on ne connaissait pas la masse et donc on ne l’a pas vu. On a changé de machine, on a remplacé le LEP par le LHC (Large Hadron Collider) dans lequel on fait entrer en collision non plus des particules légères comme les électrons et les positrons, mais des protons qui sont plus lourds, donc il y a plus d’énergie.  En 2012, après quelques années de fonctionnement, on a vu apparaître des signaux qui sont la signature du boson de Higgs. L’annonce de la découverte a été faite le 4 juillet 2012 et cela a prouvé que cette hypothèse du champ de Higgs était la bonne, 48 ans après qu’elle ait été formulée : elle a été formulée en 1964 et elle a été découverte en 2012. 48 ans après, on a la preuve que le boson de Higgs existe et que la masse des particules élémentaires provient de l’interaction qu’elles ont avec un champ qui est partout présent dans le vide.

Apparition du temps propre de la matière :

Alors on pourrait se dire que cela est de la physique des particules et que cela ne concerne que l’infiniment petit.  En fait, pas tout-à-fait parce que la physique des particules et la cosmologie (science des lois physiques de l’univers et de sa formation) sont reliées : quand on recrée les conditions du passé, on en apprend sur l’univers tel qu’il était dans ses phases primordiales. Quand on essaye de comprendre ce qui s’est passé dans l’histoire de l’univers, on est amené à concevoir que, dans l’univers primordial, le champ de Higgs n’existait pas, donc les particules élémentaires n’avaient pas de masse et elles se déplaçaient à la vitesse de la lumière. En théorie de la relativité, quand une particule n’a pas de masse, elle n’a pas de temps propre, il n’y a pas de référentiel qui lui soit associé dans lequel on puisse définir un temps pour cette particule. Donc, il n’y avait pas de temps propre aux particules et l’idée, c’est que tout d’un coup, le champ de Higgs est apparu et s’est installé partout dans l’espace. Dès qu’il est apparu, les particules qui jusque-là n’avaient pas de masse se sont couplées à ce champ, plus ou moins fortement, cela leur a donné une masse non nulle qui a engendré pour elles un temps propre. L’apparition du champ de Higgs et des bosons associés, c’est l’apparition du temps de la matière, pourrait-on dire.

Origine de l’apparition du champ de Higgs et du temps de la matière :

Qu’est-ce qui a fait que le champ de Higgs est apparu ? C’est ce qu’on appelle dans le jargon des physiciens, une brisure spontanée de symétrie. Qu’est-ce que c’est une brisure spontanée de symétrie ? Prenons un objet cylindrique positionné verticalement dans l’espace. Ce cylindre a un axe de symétrie vertical. Au moment où on laisse tomber ce cylindre, il va tomber dans une certaine direction, il va réduire son énergie, et en ce faisant, il bascule hors de son axe vertical et va briser la symétrie qui existait au départ. Avant que le cylindre ne tombe, il y avait une invariance par rotation de celui-ci autour de son axe vertical et à la fin, il y a une direction privilégiée qui a été choisie. Donc l’état final est moins symétrique que l’état initial : il y a une brisure spontanée de symétrie. On pense que c’est un phénomène de ce type-là qui a engendré l’apparition du champ de Higgs et donc a fait démarrer le temps de la matière.

Le modèle standard de la physique des particules est complet :

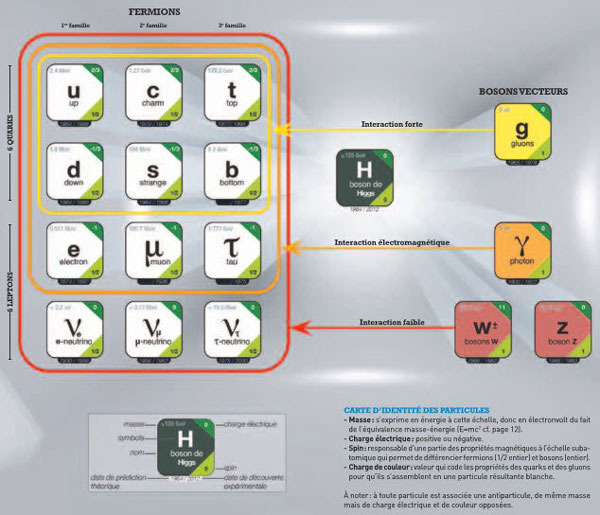
Fig. 12 : Modèle standard de la physique des particules. Source : graphisme CEA (Commissariat à l’Énergie Atomique et aux énergies alternatives).

Hiroshima le 6 août 1945 et Nagasaki le 9 août 1945, une association injuste avec Albert Einstein et la découverte de sa formule E = mc² :

Enfin, cette formule, elle est plutôt associée, dans l’imaginaire collectif, au pacte faustien que la physique la plus abstraite aurait passé avec le mal le plus concret. Bref, elle est associée à la bombe atomique, c’est-à-dire à Hiroshima et Nagasaki. Et cette association est quelque peu injuste parce que l’idée de la bombe atomique n’est apparue dans l’esprit des physiciens qu’en 1939 après une découverte qui a été faite tout-à-fait par hasard par Lise Meitner et Otto Hahn : ils ont découvert qu’il existait un isotope de l’uranium, l’uranium 235 (U²³⁵) qui a la propriété singulière de pouvoir se couper en deux, fissionner lorsqu’il est percuté par un neutron lent.  Et cela, ça n’avait été prédit par personne. La formule d’Einstein ne permettait pas non plus de le prévoir : elle date de 1905. L’uranium est connu depuis la révolution française (il a été découvert en 1789 par le chimiste prussien Martin Heinrich Klaproth). Il ne suffisait donc pas d’avoir la formule et l’uranium pour penser à la bombe atomique. Il a fallu cette découverte faite à la fin de l’année 1938 pour que les physiciens commencent à y penser.

L’idée de la bombe atomique va donc conduire à ce qu’Einstein, qui ne s’est jamais intéressé aux forces nucléaires, sollicité par des amis physiciens, va écrire une lettre au président Roosevelt dans laquelle il signale que les allemands ont des stocks d’uranium, ont également à leur disposition des très grands physiciens et les nazis pourraient être capables un jour de fabriquer la bombe atomique. Donc il agit comme une espèce de lanceur d’alerte pour le président Roosevelt.

L’association entre E = mc² et la bombe atomique ne viendra se montrer, si l’on peut dire, s’imposer qu’en juillet 1946 à la une du magazine « Time » qui vient commémorer l’anniversaire de la première explosion atomique qui avait eu lieu en juillet 1945, donc avant Hiroshima et Nagasaki dans le désert du Nouveau Mexique. Sur la couverture, on voit le visage d’Einstein qui est grave, qui semble interroger la postérité. On voit l’océan avec dessus beaucoup de bateaux de guerre, on voit un nuage atomique à la forme d’un cobra, dans le nuage même est écrite la formule E = mc² et le titre qui apparaît à cette une est « Einstein le cosmoclaste, Einstein, le destructeur de l’ordre ».

C’est à partir de cette image de couverture que nous pensons l’association entre la bombe atomique et la formule E = mc² alors que cette formule intervient dans beaucoup d’autres processus, par exemple le craquage d’une allumette, ou bien la chute d’un corps.

Conclusions :

C’est grâce au génie d’Albert Einstein et de la découverte de sa formule E = mc² en 1905 que l’on peut comprendre aujourd’hui que 99 % de la masse de la matière est due à l’énergie d’interaction qui existe entre les particules élémentaires qui sont présentes dans la structure fondamentale de la matière.

C’est grâce à la découverte du boson de Higgs en 2012 que l’on peut comprendre que la masse des particules élémentaires qui ne représente que 1 % de la masse d’un corps, cette masse est due à l’interaction des particules élémentaires avec le champ de Higgs qui remplit tout l’espace vide, qui du coup n’est pas vide.

Je vous propose cet article dans sa version numérique que vous pouvez télécharger.
EMC2.pdf (5367 téléchargements )
Vignette : https://www.wallpaperflare.com/

 par Jean-François Flamée | ON4IJ