Introduction
Traduction partielle et libre avec adaptation de l’article : « Determination of Dielectric Constant of Printed Circuit Boards » de Sam Wetterlin 1/24/10.
Remarque : L’auteur Sam Wetterlin a été contacté par email : swetterlin@comcast.net pour lui demander l’autorisation de la publication de la traduction de son article sur ce sujet.
La connaissance de la constante diélectrique des matériaux des circuits imprimés est essentielle pour déterminer la largeur de piste nécessaire pour produire une impédance caractéristique de 50 ohms ou une autre impédance souhaitée. Le matériau le plus couramment utilisé est le FR-4, sa constante diélectrique peut varier grandement entre les fabricants ou les bains, elle varie également selon la fréquence .Il est utile de disposer d’une méthode pour déterminer la constante diélectrique d’une platine particulière de façon à utiliser cette platine avec précision.
Techniquement, Nous recherchons la constante diélectrique relative (εr) ; c.à.d. la constante diélectrique relative à la valeur de la constante diélectrique du vide. Nous l’appellerons ici ε.
La constante diélectrique est parfois appelée dans la littérature : Er. K ou Dk.
Une quantité qui y est reliée est la permittivité relative, elle contient une partie réelle et une partie imaginaire, la partie réelle représente la constante diélectrique et la partie imaginaire est le facteur de perte. Le rapport entre le facteur de perte et la constante diélectrique est connu sous le terme tan(d) facteur de dissipation.
Nous nous sommes surtout intéressés à la constante diélectrique, bien que le facteur de dissipation possède un effet sur le coefficient Q à la résonnance, nous le verrons, a une incidence sur la détermination du ε.
Nous présentons ici une méthode non destructrice pour mesurer la constante diélectrique d’une platine imprimée particulière.
Nous présentons en premier lieu une méthode simple utilisant la mesure de la capacité qui est utile en certaines circonstances.
Toutes les mesures présentées dans le document de Sam Wetterlin qui est ici traduit, adapté et agrémenté par les expérimentations de ON1EV sont réalisées avec un analyseur de réseau vectoriel HP 8753B (éventuellement avec l’accessoire de test de transmission et réflexion HP 8502B), un LCR-mètre HP 4262A et un LC-mètre IIB AADE (Almost All Digital Electronics). La méthode de mesure de la résonnance par le coefficient de transmission (S21) ne nécessite pas la mesure de la phase et est donc réalisable au moyen d’un analyseur de spectre équipé d’un générateur de poursuite (mesure scalaire), ou même au moyen d’un générateur et d’un bolomètre (mesureur de puissance).
La méthode de la capacité.
La capacité de deux plaques parallèles (les surfaces cuivre du circuit imprimé double face) avec une surface A exprimée en pouces carrés et distant de D exprimé en pouces est déterminée par la constante diélectrique du matériau situé entre elles.
La formule est la suivante pour une valeur de capacité donnée en pF :
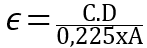(Eq. 1) (Eq.1 : extrait de l’article de Sam Wetterlin).
Il existe une imprécision dans cette formule, celle-ci est due à l’effet de frange qui se manifeste au bord du circuit imprimé. Cependant lorsque l’on découpe du circuit imprimé FR-4 de 1.6mm d’épaisseur en deux pièces aussi petites que 25,4mm x 50,8mm (1 pouce x 2 pouces) avec une lame de rasoir (lame de cutter) de telle manière qu’il n’y ait pas de perte de matière ; il en résulte deux pièces (deux condensateurs) dont la capacité totale équivaut celle d’origine avant découpe. Ainsi, l’augmentation de la longueur totale du bord (celle de la somme des périmètres respectifs) a un effet minimal.
Le principal défaut de cette formule est qu’un circuit imprimé de plusieurs pouces de long ou de large ne constitue pas un composant très bien localisé excepté à des fréquences assez basses, généralement à des fréquences situées bien en dessous de celles où l’on utilisera ce circuit imprimé pour réaliser un micro-ruban dont l’impédance exacte est critique.
Cependant il s’avère qu’un circuit imprimé peut être modélisé comme un condensateur à capacité localisée qui est mis en série avec une inductance de faible valeur.
Valeur résiduelle + capacité réelle@10KHz Photo : ON1EV
Valeur résiduelle avant mesure Photo : ON1EV
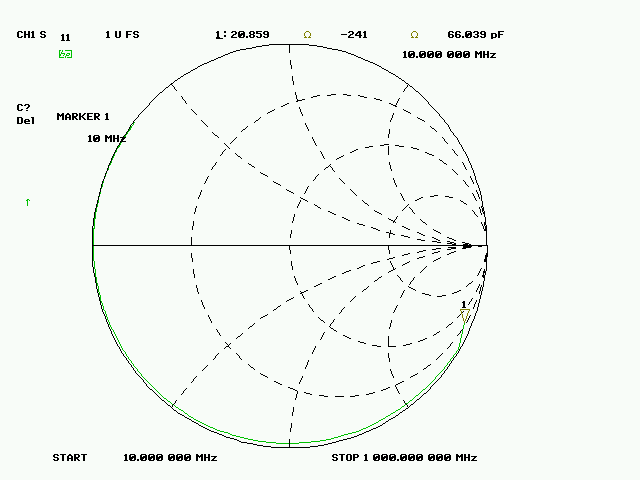
Fig. 1 : La Capacité vaut 66 pF à 10 MHz. Cliché : ON1EV.
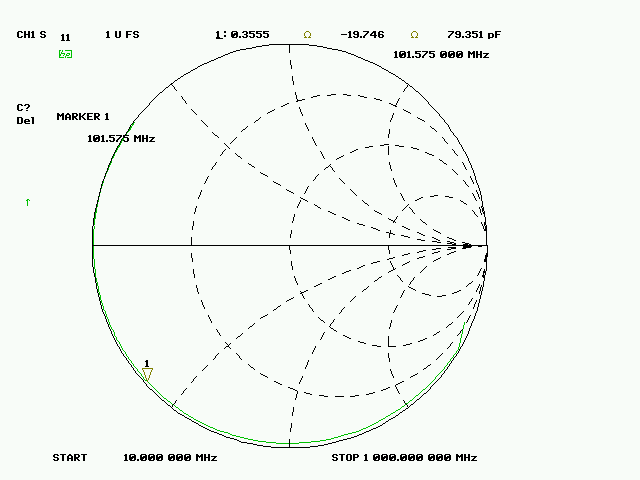
Fig. 2 : La Capacité vaut 73 pF à 101 MHz. Cliché : ON1EV.
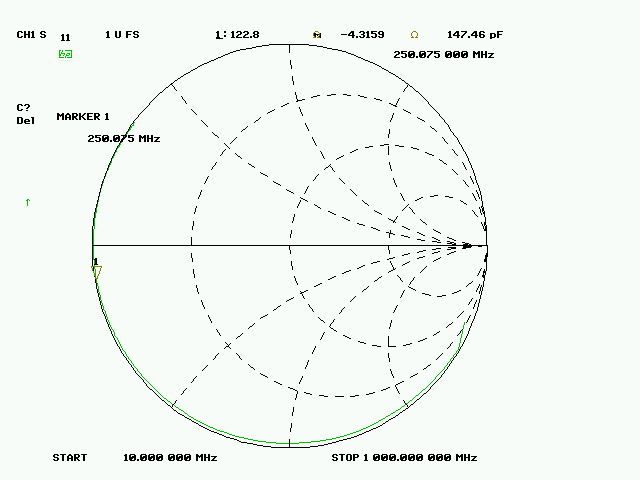
Fig. 3 : La Capacité vaut 147 pF à 250 MHz. Cliché : ON1EV.
Les figures 1, 2 et 3 illustrent les mesures effectuées sur un CI (circuit imprimé) de 1,1 pouce de côté, en utilisant l’analyseur de réseau HP 8753B en mode réflexion avec un balayage en fréquence allant de 10 MHz à 1000 MHz. Cette mesure a été réalisée avec un connecteur SMA pour circuit imprimé qui se glisse sur le côté de celui-ci.
Photo 1 : circuit imprimé double face de 1,1 pouce de côté et équipé d’un connecteur SMA. Photo : ON1EV.
La capacité est relativement stable jusqu’à 100 MHz, mais ensuite elle augmente jusqu’à la résonnance ; au-delà de la résonnance la capacité devient une self.
En réalité la capacité mentionnée ne subit pas de transformation mais l’inductance série présente fait apparaître un changement de capacité. Le problème est que nous observons un circuit LC série comme s’il s’agissait d’un condensateur ce qu’il n’est pas.
Une manière de traiter cet effet de l’inductance est de la diminuer. En plaçant le connecteur de test au centre de la platine (avec le corps du connecteur bien soudé d’un côté et le conducteur central placé au travers d’un petit trou foré dans le CI et soudé sur l’autre face.) réduira l’inductance et sera plus encore plus efficace si le CI sera découpé en forme circulaire avec le connecteur au centre.
Une alternative consiste à mesurer la partie inductive au moyen de l’analyseur de réseau vectoriel. On procède ensuite à une suppression de l’effet de l’inductance par calcul mathématique.
L’appareil HP 8753B dispose d’un affichage des valeurs réelles et imaginaires de l’impédance complexe sur l’abaque de Smith, ce qui permet d’obtenir les valeurs de R, de L et/ou C qui modélise le CI sous la forme d’un circuit RLC.
Ce modèle identifie la capacité, l’inductance et l’impédance. Les figures 1, 2, 3, 4 indiquent les résultats de l’analyse. […]
Au-delà d’une certaine fréquence le condensateur augmente en apparence, ensuite l’inductance devient prépondérante.
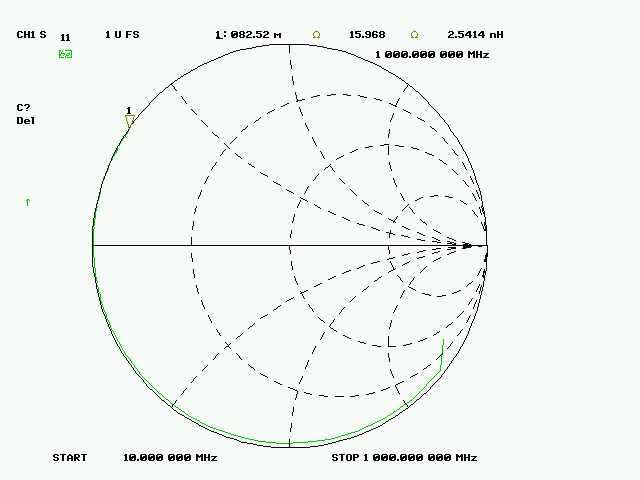
Fig. 4 : La valeur de l’inductance vaut 2,5 nH à 1GHz Cliché : ON1EV.
L’analyse nous indique un condensateur de 66 pF @10 MHz, de cette mesure l’on peut calculer la valeur de la constante diélectrique : 4,84 (Eq. 1)
L’épaisseur du CI n’est pas toujours bien précisée. Si nous voulons construire un micro-ruban, d’une impédance caractéristique spécifique nous avons besoin de connaître aussi bien l’épaisseur du substrat du CI que la constante diélectrique de celui-ci. La méthode de la capacité peut être utilisée pour déterminer l’épaisseur du CI à condition que l’on connaisse déjà la constante diélectrique (cette constante peut être évaluée avec la méthode de la résonnance).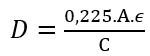
(Eq. 2) (Eq.2 : extrait de l’article de Sam Wetterlin).
Références.
La méthode de la résonance utilisée ici vient de trois sources :
- S. Napoli and J. J. Hughes, “A Simple Technique for the Accurate Determination of the Microwave Dielectric Constant for Microwave Integrated-Circuit Substrates”, IEEE Transactions on Microwave Theory and Techniques, July, 1971.
- Howell, “A Quick Accurate Method to Measure the Dielectric Constant of Microwave Integrated-Circuit Substrates”, IEEE Transactions on Microwave Theory and Techniques, March, 1973.
- Wang, “Determining Dielectric Constant and Loss-Tangent in FR-4”, UMR EMC Laboratory Technical Report TR-00-1-041, March, 2000.
Chacun de ces articles traitent des substrats comme des cavités résonnantes et déterminent la constante diélectrique à partir de la résonnance de ces cavités. Elles sont connues sous les noms des auteurs « Napoli/Hughes », « Howell » et « Wang ».
De plus, plusieurs méthodes de test sont disponibles sur le site IPC. : http://www.ipc.org/ContentPage.aspx?pageid=ELECTRICAL-TEST-METHODS
La Section 2.5.5.6 de cette page Web décrit la méthode de la résonnance; la section 2.5.5 décrit la méthode para capacité.
Mathématique des cavités.
Dans une cavité essentiellement à deux dimensions avec une certaine longueur et une certaine largeur, mais d’une très faible épaisseur, plusieurs résonances sont possibles. Les résonnances les plus simples ont lieu à des fréquences où la demi-longueur d’onde coïncide soit avec la longueur soit avec la largeur de la cavité, mais il existe plusieurs autres possibilités. Chaque résonnance correspond à la valeur d’un nombre entier du nombre d’onde ou du nombre de mode, c’est-à-dire le rang du mode dans chaque direction (largeur et longueur). Si p est le rang du mode dans la direction de la longueur (L) et si q est le rang du mode dans la direction de la largeur, alors la fréquence de résonnance pour un p et un q donné est :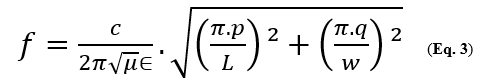
L et W en [m] et f en [Hz]. (Eq. 3 : extrait de l’article de Sam Wetterlin).
Où c est la vitesse de la lumière, µ est la perméabilité (pour les circuits imprimés c’est 1) et ε (epsilon) est la constante diélectrique. Chacune des valeurs de p et q sont des nombres entiers non négatifs excepté qu’ils ne peuvent être nuls simultanément.
Pour mesurer L et W en [pouce] et f en [MHz] nous convertissons la formule sous cette forme :
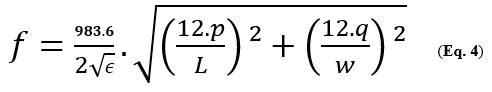(Note: la vitesse de la lumière est 983,6 millions de pied par seconde). (Eq. 4 : extrait de l’article de Sam Wetterlin).
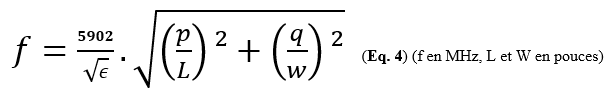Avec f en [MHz], L et W en [pouces].(Eq. 4 : extrait de l’article de Sam Wetterlin).
(Note: la vitesse de la lumière est de 983,6 millions de pieds par seconde).
Ces équations peuvent sembler impressionnantes, mais il existe deux situations où leur signification est très évidente. Si q est 0 alors il n’y a pas de résonnance dans la direction de la largeur et la résonnance est entièrement déterminée par la longueur. Cette équation prend la forme de ceci :
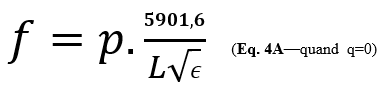(Eq. 4A : extrait de l’article de Sam Wetterlin).
Tout ce qui se trouve sur le côté droit de l’équation sauf p représente la fréquence dont la demi-longueur d’onde est égale à L/12 pied. C’est la raison pour laquelle les différentes fréquences de résonnance sont des multiples entiers (ce multiple étant p) de cette fréquence dont on donne la demi-longueur d’onde.
De manière similaire si p est égal à 0, la résonance est totalement dans la direction de la largeur à des multiples (q) du fondamental de la fréquence de résonnance donnée par la demi-longueur d’onde de la largeur.
Si nous considérons la longueur comme la plus grande dimension, nous savons que la fréquence de résonnance la plus basse sera égale à la demi-longueur d’onde qui correspond à la longueur du CI, tel que p = 1 et q = 0.
Si ε est constant, il existera des résonnances aux multiples de cette fréquence, avec p=N (N est un entier) et q = 0. Un ensemble de résonnance existera de manière similaire si p = 0 et q = N. D’autres fréquences de résonnance sont entremêlées parmi celles qui agissent selon la longueur ou la largeur et ces autres fréquences de résonnance agissent selon les deux directions à la fois. Pour ces autres fréquences, p et q sont tous les deux différents de zéro.
Si la longueur et la largeur sont identiques, les deux premières fréquences de résonnance apparaîtront à la même valeur. Si la largeur est plus petite que la longueur d’au moins 58% (1 sur la racine carrée de 3), la seconde résonnance tombera sur la fréquence fondamentale selon la dimension de la largeur (p = 0, q = 1) et la troisième sera une résonnance combinée avec p = q = 1. Pour des largeurs plus étroites, il existe toute sorte de possibilité pour les ordres de résonnances. Pour des largeurs très étroites, les quelques premières résonnances seront totalement déterminées par la dimension de la longueur ave p = 1, 2, 3… et q = 0.
Si nous mesurons la fréquence de résonnance f pour un p et q donnés nous pouvons calculer la constante diélectrique comme suit :
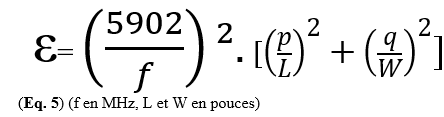(Eq. 5 : extrait de l’article de Sam Wetterlin).
Si L et W sont en [cm], le facteur 5902 doit être augmenté à la valeur de 14990.
Le fait qu’il y ait autant de résonnances possibles nous conduit à mesurer ε sur une large gamme de fréquences pour un seul circuit imprimé.
Pour la précision la plus élevée, Howell et Wang ont calculé un facteur de correction qui tient compte des pertes basé sur le Q à la résonance. La fréquence mesurée est ajustée selon la formule suivante et c’est cette fréquence qui est utilisée dans l’équation n° 5.
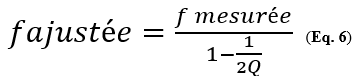(Eq. 6 : extrait de l’article de Sam Wetterlin).
Notez que pour la valeur de Q = 50 (la valeur approximative pour le FR-4), le dénominateur est 0,99, qui par conséquent augmente la fréquence de 1 % et provoque ainsi une diminution de la valeur calculée pour ε de 2% (car la fréquence est portée au carré dans l’équation n° 5). Pour des valeurs de Q supérieures à 100 il n’y a certainement pas lieu de s’inquiéter car l’erreur devient négligeable.
Application aux platines de circuits imprimés.
Un Circuit Imprimé à double face peut être traité comme une cavité dont les côtés sont ouverts, ainsi pour l’instant nous considérons que c’est le cas. Si une face est traitée comme plan de masse, le signal peut être couplé faiblement à l’autre face, créant ainsi un signal qui se propage principalement entre les deux faces dans le diélectrique du CI. Si nous mesurons certaines fréquences de résonnance de cette cavité, nous pouvons calculer la constante diélectrique à partir de l’Eq.5. Nous effectuerons dans un premier temps les mesures selon le mode transmission, c’est-à-dire des mesures du coefficient de transmission (S21).
Une pièce de circuit imprimé est découpée suivant les dimensions suivantes : 4 x 5 pouces.
Des connecteurs SMA sont soudés sur les coins opposés. Ils doivent être soudés d’un seul côté (Masse) et le conducteur central doit être laissée libre au-dessus du plan de cuivre supérieur : faible couplage capacitif.
Voir photos ci-dessous.
Remarque importante : ne pas caler le connecteur SMA contre le CI car les deux faces seraient alors en contact, laisser un petit jeu entre la plaque et le connecteur SMA).
Photos 2 et 3 : réalisation de la platine de CI pour le test de transmission. Photos : ON1EV.
Le premier port de mesure de l’analyseur (port de stimulation) est raccordé au premier connecteur SMA et le second port de mesure (port du récepteur de mesure) est raccordé au second connecteur SMA. D’une manière optionnelle, on peut intercaler des atténuateurs de l’ordre de 3 dB à l’entrée et à la sortie du circuit imprimé sous test afin de résorber d’éventuels échos de signaux dans les câbles de mesure.
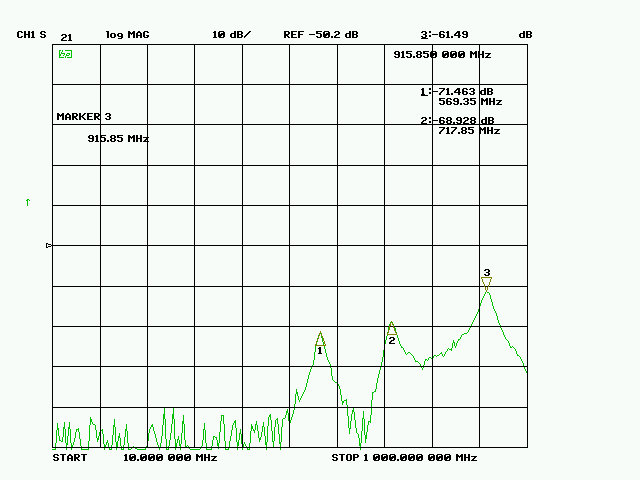
Fig. 4 : Transmission du FR-4 de coin à coin. Cliché : ON1EV.
Les données situées à moins de -90 dB sont essentiellement du bruit ; cela correspond au niveau du plancher de bruit de l’appareil de mesure dans les conditions de la résolution de bande passante qui est paramétrée.
Il existe 3 résonnances qui sont illustrées sur le cliché de mesure à la figure 4. Le marqueur 1 indique la fréquence de résonnance pour laquelle la demi-longueur d’onde correspond à la dimension la plus grande (longueur). Le marqueur 2 indique la fréquence pour laquelle la demi-longueur correspond à la dimension la plus petite (largeur). Si nous choisissons la longueur comme la dimension la plus grande et que nous nommons le mode comme ceci M(p,q), alors le marqueur 1 indique le mode de résonnance M(1,0) et le marqueur 2 indique le mode de résonnance M(0,1). Le marqueur 3 indique la fréquence où apparaît le premier mode de résonnance combinée qui implique les deux directions, c’est-à-dire à la fois la longueur et la largeur du CI ; il s’agit ici du mode M(1,1).
Cette notation pour les modes est différente des notations habituelles TE10 (transverse électrique dans cet exemple), etc. Pour nos besoins, nous nous soucions seulement que chaque mode soit identifié par deux entiers que nous utiliserons dans l’équation n° 5. Nous ne nous intéressons pas aux détails de la propagation du signal. Si nous appliquons Eq. 5, à chacune de ces résonnances, en utilisant les valeurs de f, p et q pour chacune d’elles, nous obtenons la constante diélectrique pour les marqueurs 1 et 2 d’une part et pour le marqueur 3 d’autre part.
L’ajustage grâce à l’équation n° 6 en connaissant la valeur Q égale à 37 réduira respectivement ces valeurs de 6,3% à 4,26 et 4,16. (Le coefficient Q a été mesuré séparément en mesurant les valeurs à -3dB de la résonance et vaut 37.) Cette valeur est plausible pour ces fréquences, comme la constante diélectrique varie très fort entre les différentes platines, nous ne pouvons pas juger de la précision de la méthode à partir de ces données.
Une remarque supplémentaire concernant ce Q de 37, il s’agit d’un Q modeste ce qui explique la correction plus grande de la valeur diélectrique.
Nous pouvons aussi effectuer les mesures de transmission d’une autre manière : en faisant circuler le signal d’une face à l’autre sans qu’aucune ne soit raccordée à la masse. Cette mesure fonctionne au mieux si la connexion est réalisée au coin de la plaque. Les connexions des câbles rigides sont illustrées sur la photo suivante.
Photo 4 : préparation des extrémités des câbles de mesure pour effectuer les mesures de transmission face à face du circuit imprimé sous test. Photo : extraite de l’article technique de Sam Wetterlin.
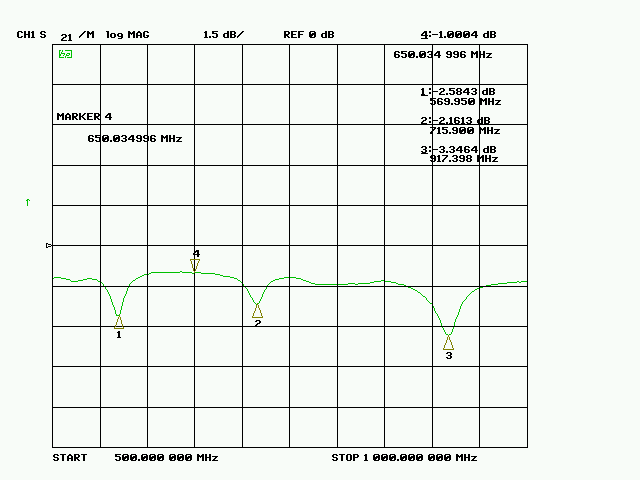
Fig. 5 : mesures de transmission face à face du circuit imprimé. Cliché : ON1EV.
Pour faire correspondre les résonnances mesurées aux modes spécifiques, nous calculons en premier lieu la constante diélectrique au départ des trois premières résonnances qui sont faciles à identifier.
Ce calcul donne une valeur approximative égale à 4,3 ainsi nous pouvons estimer que c’est la valeur réelle et nous pouvons aussi calculer les fréquences où les résonnances doivent se trouver. Nous faisons ensuite correspondre les résonnances réelles avec les valeurs calculées du mieux que l’on peut. Voir la table 1.
Table 1- Valeurs calculées et valeurs réelles des modes de résonances du circuit 5” x 4” FR-4 à partir des mesures de transmission
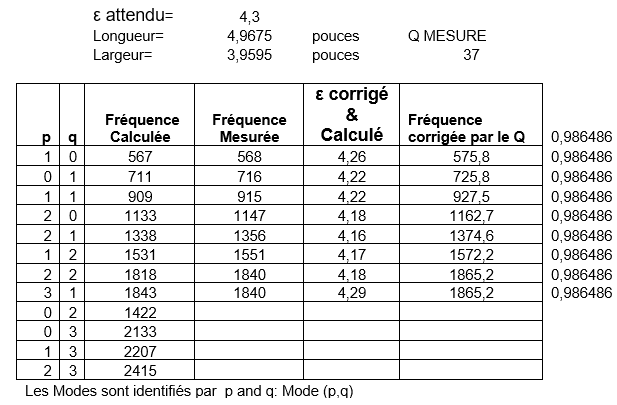
Les 2 colonnes de gauche du tableau listent les résonnances par mode ; la liste de droite est classée par ordre croissant de fréquences, les deux colonnes de gauche contiennent les valeurs p et q, p étant le rang du mode qui correspond à la dimension de la longueur. La troisième colonne est la fréquence à laquelle apparaît le mode pour lequel ε = 4,3. Cette colonne est utilisée pour faire correspondre le mode au pic de résonnance spécifique ; la fréquence réelle est celle qui est mesurée et qui apparaît dans la quatrième colonne. Finalement à partir de la fréquence mesurée nous allons calculer la valeur de ε, cette valeur apparaît dans la cinquième colonne. La fréquence mesurée de 1840 MHz apparaît deux fois dans la table et peut prêter à une certaine ambiguïté car on ne peut dire si cela correspond à M(1,3) ou bien à M(3,2) ; cependant les valeurs calculées des ε restent proches de la valeur donnée par le constructeur.
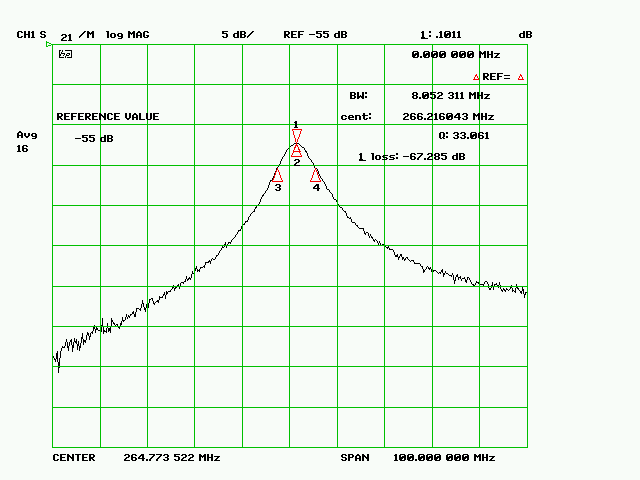
Mesure du Coefficient de qualité Q en calculant la largeur de bande de la courbe de résonnance :
Q = 266MHz/8.052= 33. Cliché : ON1EV.
La table 1 montre que nous pouvons retrouver et faire correspondre la plupart des pics de résonnance aux modes résonnants spécifiques et la constante diélectrique varie de 4,26 à 4,16 ce qui correspond à une erreur de -2,3% au maximum. On constate que la valeur de la constante diélectrique décroit au fur et à mesure que la fréquence augmente, remarquez que dans le tableau, la correction apportée par l’influence de la valeur Q = 37 est intégrée.
FR-4 Variation de la constant diélectrique.
On remarque que l’adéquation de la table 1 laisse à désirer pour les fréquences élevées, la constante diélectrique varie avec la fréquence, pour obtenir un tableau qui respecte la théorie, le circuit imprimé doit être beaucoup plus long que large. Le tableau 2 montre la variation importante de la constante diélectrique. Le circuit utilisé est de la dimension suivante :
12 "x 1,5" x 0,020"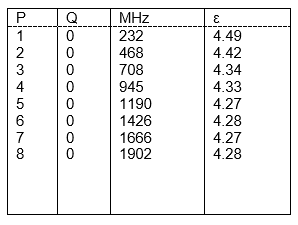
Soit une diminution de 4,8 %
Table 2—Résonances d’un CI 12” x 1.5”x 0,020” FR-4
Le test a été conduit avec du NELTEC 9250, celui-ci possède un ε très stable et bien contrôlé. De 2,50+/- 0.02 la première résonance a été examinée afin d’établir le coefficient de qualité.
Ensuite un balayage a été effectué pour remplir le tableau de calcul Excel.
Mesure du Q (coefficient de qualité).
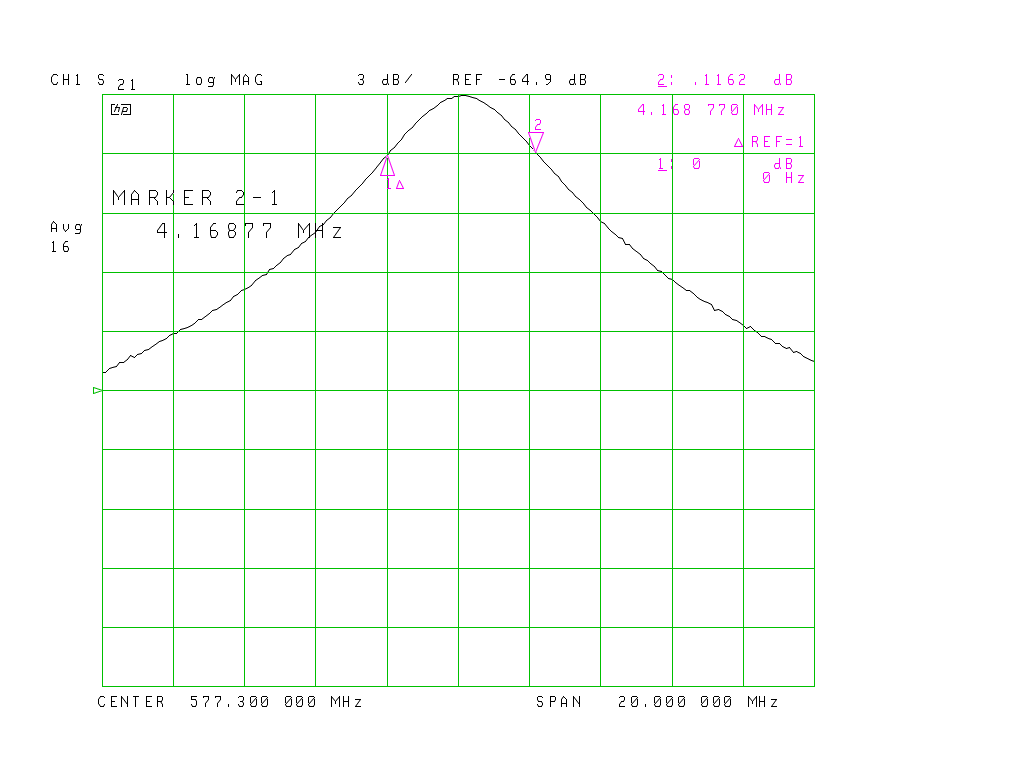
Mesure du coefficient Q de la plaque Neltec 9250 à 579 Mhz La bande mesurée est 4,168 Mhz à 3dB. Cliché : ON1EV.
DETERMINATION de la constante diélectrique des circuits imprimés
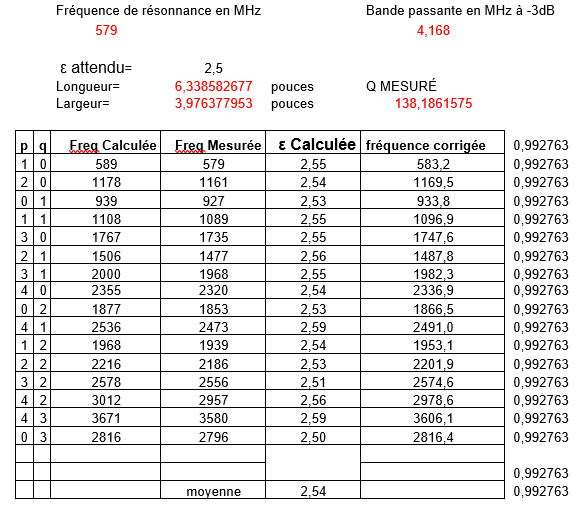
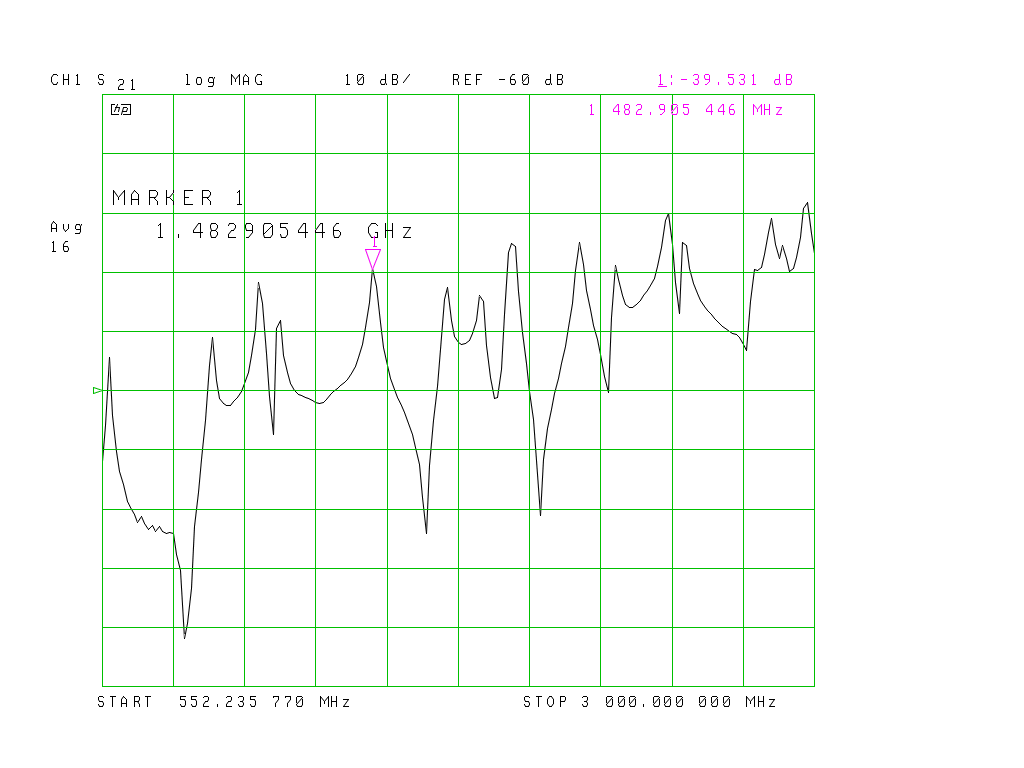
Le balayage effectué par l’analyseur de réseau (FIG 9) Cliché : ON1EV..
Conclusions
La méthode ci-décrite pour le calcul de la constante diélectrique à partir des fréquences de résonnance mettant en œuvre un procédé non destructif basé sur des mesures de transmission laisse apparaître que cette méthode offre des mesures précises. Lorsque l’on procède à des mesures sur du FR-4, la précision est probablement améliorée en réduisant de 2 % la valeur de la constante diélectrique obtenue par calcul de façon à tenir compte des pertes dues principalement par le facteur de dissipation dans le matériau.
Avec cet ajustement, l’erreur dans le calcul de la constante diélectrique est principalement de l’ordre de seulement 1 à 2 %. D’un certain point de vue, l’impédance caractéristique d’un micro-ruban de 50 Ohms calculé à partir d’une valeur ε = 3, cette impédance va diminuer de seulement 1 Ohm par rapport à celle qui se serait avérée à une valeur de 3,15 c’est-à-dire une erreur de 5 % sur la valeur de ε. Une erreur de plusieurs pourcents sur la valeur calculée de la constante diélectrique est dès lors tout-à-fait acceptable.
Vignette : https://www.piqsels.com/fr
Traduction partielle et libre avec adaptation de l’article par Guerrino Daipra ON1EV
Cet article peut être téléchargé au format PDF. Il suffit de cliquer sur ce lien :
A propos de l'auteur
