Après l’intérêt rencontré par « Le B.A. BA de la Ligne d’Alimentation », il serait intéressant, à la suite de ces deux articles, de mettre en pratique les principales notions développées.
Contenu :
1 - Introduction
2 - Quelles sont les premières questions à se poser lors de l’installation d’une antenne ?
3 – Historique
3.1 - L’adaptation de l’impédance de l’antenne à l’impédance de la ligne qui l’alimente
3.2 - Qu'est-ce que l'adaptation d'impédance ?
3.3 - Le R.O.S. mètre
4 – Pourquoi le VNA ?
4.1 - Un analyseur vectoriel, c’est quoi ?
4.2 - L’Abaque de Smith
4.3 - Le VNA intègre un Micrologiciel
4.4 - Que pouvons-nous obtenir avec un NanoVNA ?
4.5 - Le NanoVNA est à la fois un émetteur et un récepteur.
5 - Les paramètres « S »
5.1 - Les Paramètres S et le réseau à deux ports et deux directions
5.2 - Le NanoVNA est un système de mesure à deux ports et dans une seule direction.
6 – La fonction du canal ch0 du NanoVNA
6.1 - La Perte de Retour (Return Loss)
7 - Comprendre les grandeurs électriques calculées et les relations qui les lient.
7.1 - Le Rapport de l’Onde Stationnaire de tension (R.O.S)
7.2 - Le coefficient de réflexion de tension « ρL » à la jonction antenne
7.3 - Le coefficient de réflexion de puissance « ρL2 » à la jonction antenne
7.4 - Perte d’insertion de la ligne de transmission
7.5 - Perte d’insertion(dB) comparée au coefficient d’atténuation de puissance.
8 – Les Mesures
8.1 – La perte d’insertion de la ligne à l’adaptation
8.2 - Perte coaxiale calculée directement en termes d'impédance
8.3 - Mesure de l’atténuation de la ligne par la méthode indirecte
8.4– Mesurer la perte d’insertion d'un tuner d'antenne
9 - La fonction du canal ch1 du NanoVNA
10 – Mise en œuvre du NanoVNA
10.1 – L’Étalonnage
11– NanoVNAsaver
12 – Résumé13 – Annexe 1 et 2
1 - Introduction
Le VNA pour « Analyseur Vectoriel de Réseau » permet de mettre en lumière les différents paramètres qui régissent le fonctionnement électrique de nos systèmes d’antennes et circuits HF, bien mieux que le vénérable R.O.S-mètre connu de tous.
Le sujet du rayonnement proprement dit de l’antenne ne sera pas abordé dans le présent article, car cette matière demande un développement différent sur ce qui fait que nos antennes rayonnent.
Il y a donc lieu de ne pas confondre rendement électrique du système d’antenne et performance (gain) du rayonnement électromagnétique de l’antenne.
L’évolution technologique nous propose actuellement à des prix très modérés des équipements dont les performances sont largement adaptées à nos besoins radioamateurs, face aux appareils professionnels financièrement inaccessibles pour la majorité d’entre nous. Sans faire de promotion commerciale de l’un ou l’autre, je citerai le NanoVNA générique, qui aujourd’hui fait partie de l’équipement des nombreux radioamateurs dont la seule motivation n’est pas d’empiler des QSL’s.
2 - Quelles sont les premières questions à se poser lors de l’installation d’une antenne ?
- Pourquoi les antennes ont-elles une impédance schématisée par le circuit électrique d’une résistance en série avec une réactance ?
- Pourquoi la ligne d'alimentation est-elle caractérisée par une impédance de charge ?
- Que nous dit exactement le ROS (le Rapport de l’onde stationnaire de tension) sur la "qualité" de l’adaptation entre l’impédance de la ligne d'alimentation et l’impédance d’entrée de l'antenne ?
- Le ROS mesuré à la station est-il le même (ou assez proche) de celui présent aux bornes de l'antenne ?
- Le ROS à la station peut-il être différent à une certaine fréquence plutôt qu’à une autre ?
Les fondements des réponses à ces questions sont développés dans « Le B.A. BA de la Ligne d’Alimentation » publié sur le site ON5VL.
3 - Historique
La première préoccupation, lors de la mise en service d’une antenne est de faire en sorte d’obtenir le maximum de puissance à l’antenne, le minimum de puissance en retour vers l’émetteur et le minimum de puissance perdue dans la ligne d’alimentation et ses accessoires, comme l’éventuel balun et coupleur.
3.1 - L’adaptation de l’impédance de l’antenne à l’impédance de la ligne qui l’alimente
L'antenne, dans l'environnement de son utilisation finale, doit être adaptée à l’impédance caractéristique de la ligne, afin qu'elle fonctionne avec un rendement électrique maximum dans la bande de fréquences souhaitée.
3.2 - Qu'est-ce que l'adaptation d'impédance ?
L'adaptation de l'impédance d'entrée ZL de l'antenne à l’impédance caractéristique Z0 de la ligne de transmission, le plus souvent 50 Ω, est une condition préalable pour garantir que le maximum de puissance soit transféré de la ligne à l'antenne avec une quantité réfléchie négligeable ou nulle en retour.
L’adaptation dans l’installation finale est fondamentale car l'impédance de l'antenne peut être modifiée en fonction de sa hauteur au-dessus du sol, de ses propriétés électriques, de la proximité et des propriétés des objets situés dans son environnement proche.
3.3 - Le R.O.S. mètre
Le plus connu, est en premier lieu un indicateur de la qualité, comme nous l’avons vu précédemment, de l’adaptation entre l’impédance d‘entrée de l’antenne et l’impédance caractéristique de la ligne de transmission qui lui est connectée.
Il ne mesure pas le R.O.S, mais il le « calcule » à partir du coefficient de réflexion « ρ » qui est le rapport de la mesure de l’amplitude de crête du courant réfléchi à l’amplitude de crête du courant incident à l’endroit de la ligne où il est inséré : ![]()
Celui-ci n’est rien d’autre qu’un simple détecteur de crête qui ne donne que le rapport d’amplitude entre deux courants sans aucune information sur la relation de phase entre les courants mesurés à cet emplacement.
4 – Pourquoi le VNA?
L’indicateur de ROS ne nous donne donc qu’une information limitée sur la qualité de l'adaptation de la ligne d'alimentation à l'antenne.
Que l’indicateur ROS soit monté à l'antenne elle-même ou à la station, il ne renseigne pas exactement, en composantes résistive et réactive, comment améliorer l’adaptation à l’antenne.
4.1 - Une analyse vectorielle, c’est quoi ?
Les grandeurs électriques, tension, courant, impédance, relatives au courant alternatif sinusoïdal dont la valeur instantanée est donnée par ![]() sont des grandeurs vectorielles.
sont des grandeurs vectorielles.
Pour caractériser pleinement ces grandeurs électriques nous avons besoin de plus d’informations que la simple valeur de ces grandeurs électriques. Nous avons également besoin de connaître leur décalage dans le temps et dans l’espace, décalage que l’on mesure en distance angulaire sous le nom de déphasage.
Elles peuvent alors être représentées graphiquement par des segments de droite orientés ayant une origine, une longueur, une direction et un sens dans la direction indiquée, c’est ce que l’on appelle des vecteurs.
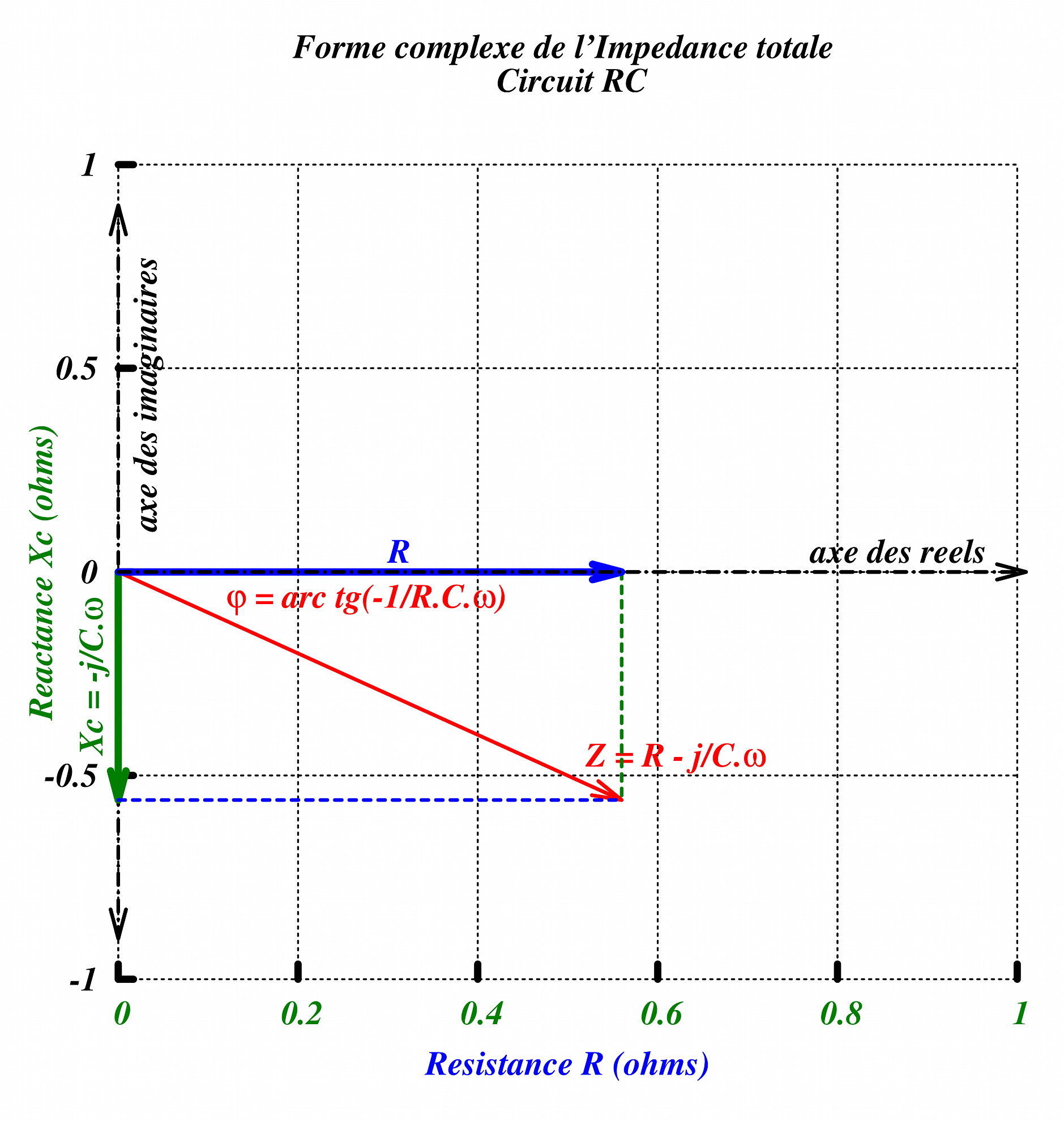
Fig.1 Exemple de diagramme de Fresnel représentant l’impédance complexe aux bornes d’un circuit RC série.
Si nous prenons l’exemple de l’impédance Z d’un circuit ou d’un composant, qui n’est autre que le résultat du rapport de l’amplitude de la tension au courant à ses bornes, cette impédance Z peut se décomposer en![]() pour les composantes en phase (I) de la tension et du courant et
pour les composantes en phase (I) de la tension et du courant et![]() pour les composantes en quadrature de phase (Q) de la tension et du courant où ± 90° est représenté dans une équation par ± j.
pour les composantes en quadrature de phase (Q) de la tension et du courant où ± 90° est représenté dans une équation par ± j.
Le symbole « j » est un nombre imaginaire ![]() car la racine carrée d’un nombre négatif est impossible. Il indique simplement que la valeur qui le suit est décalée de 90° en avance ou en retard sur la valeur qui représente les composantes en phase.
car la racine carrée d’un nombre négatif est impossible. Il indique simplement que la valeur qui le suit est décalée de 90° en avance ou en retard sur la valeur qui représente les composantes en phase.
L’impédance Z prend alors la forme « complexe » bien connue ![]()
Nous voyons sur le diagramme de Fresnel que la longueur |Z| ne s’obtient pas par la simple addition de la longueur de R et de X.
C’est l’application du théorème bien connu de Pythagore (400 ans av JC) qui calcule Z comme l’hypoténuse d’un triangle rectangle : ![]()
Toujours dans ce triangle rectangle, l’inclinaison φ du vecteur ![]() par rapport au vecteur horizontal
par rapport au vecteur horizontal ![]() pris pour référence de phase est donné par le sinus de l’angle
pris pour référence de phase est donné par le sinus de l’angle ![]() où la valeur de |X| en fonction de l’angle φ devient |X|=|Z|.sin(φ).
où la valeur de |X| en fonction de l’angle φ devient |X|=|Z|.sin(φ).
De même pour le vecteur ![]() en fonction de l’angle φ du vecteur
en fonction de l’angle φ du vecteur ![]() :
: ![]() ou la valeur de |R| devient
ou la valeur de |R| devient
|R|=|Z|.cos(φ).
L’impédance Z prend alors la seconde représentation ![]()
Il existe une troisième représentation qui fait intervenir les identités d’Euler ![]() Toutes ces représentations sont bien utiles pour « faciliter » le calcul de l’association série-parallèle d’impédances complexes.
Toutes ces représentations sont bien utiles pour « faciliter » le calcul de l’association série-parallèle d’impédances complexes.
Hors calcul, nous voyons souvent une forme plus « contractée » ![]() basée sur la tangente de l’angle
basée sur la tangente de l’angle ![]() et réciproquement la valeur de l’angle qui est donnée par la fonction inverse de la tangente
et réciproquement la valeur de l’angle qui est donnée par la fonction inverse de la tangente ![]()
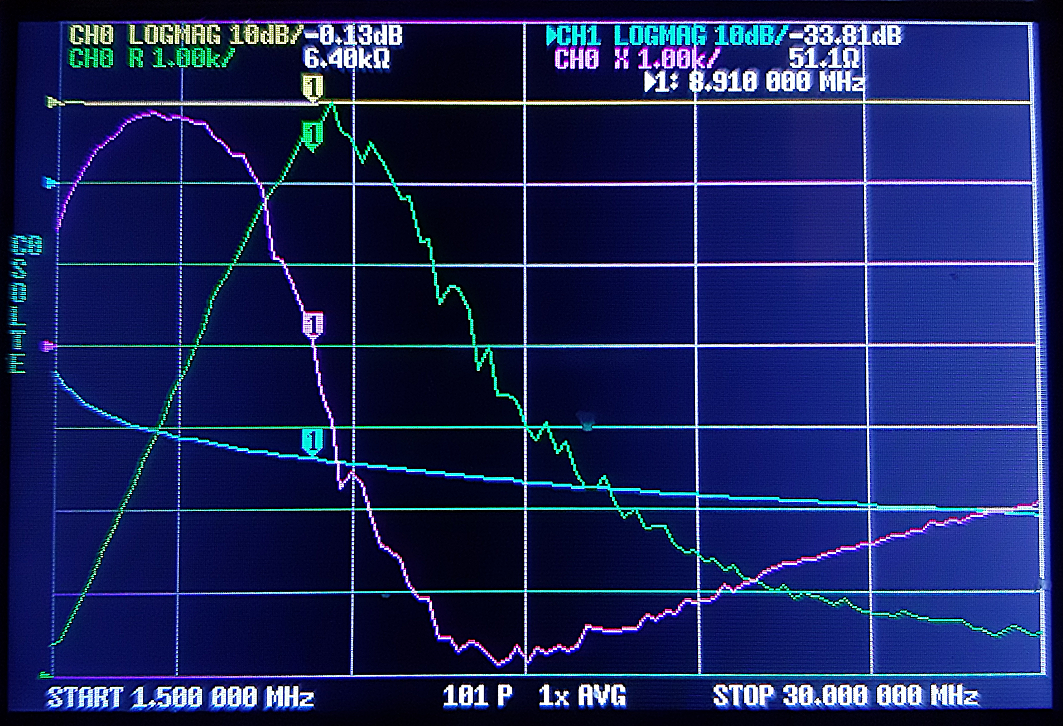
Exemple de relevé de l’impédance équivalente série de R et de jX de 1.5 MHz à 30 MHz d’un choke balun constitué de 12 tours de RG174 sur un tore FT140-43.
Les valeurs à la position du Marker «1» sont indiquées sur la ligne horizontale supérieure.
Nous voyons que le Marker « 1 » à 8.918 MHz est proche de la fréquence de résonance du circuit résonnant parallèle du balun.
Nous constatons que la résolution mathématique de ces équations complexes risque d’être longue et fastidieuse. C’est pourquoi, avant la disponibilité à faible prix d’un analyseur vectoriel, VNA, le radioamateur avait à sa disposition un outil graphique, une interface graphique, « l’Abaque de Smith », pour résoudre l’ensemble des calculs impliquant les quantités complexes liées aux paramètres de fonctionnement électrique des circuits d’alimentation de l’antenne.
4.2 - L’Abaque de Smith
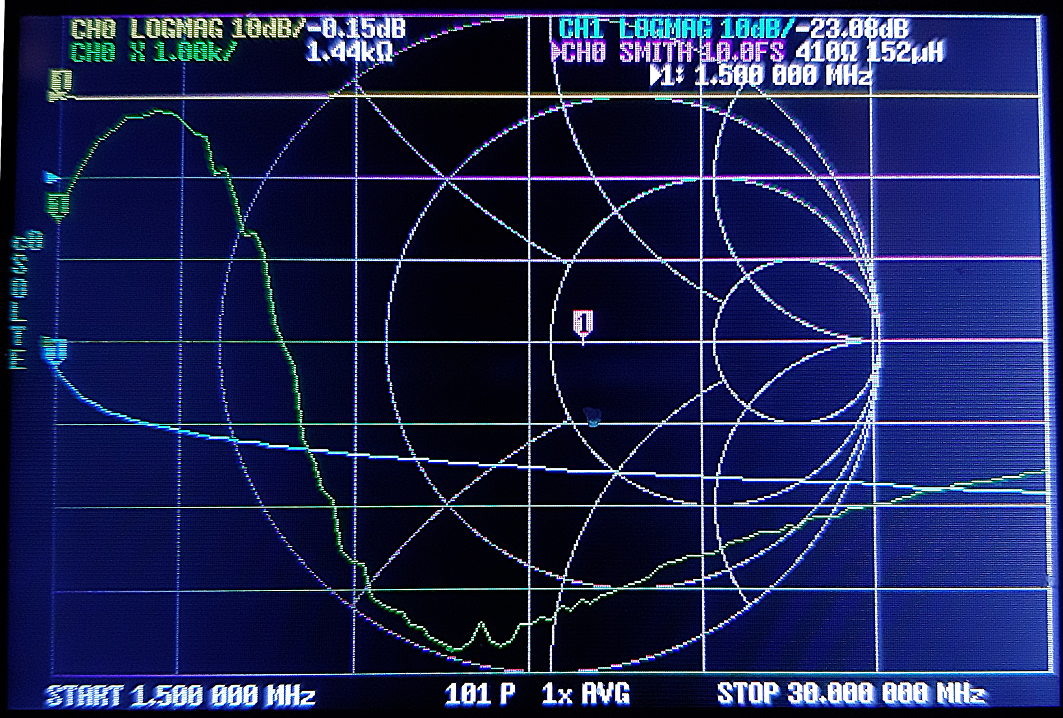
Relevé de l’impédance du même balun à l’aide de l’abaque de Smith. Le Marker «1» est positionné à 1.5 MHz.
Le diagramme de Smith fait partie du panel des formats d’affichage des paramètres analysés par le NanoVNA. Il est ainsi plus facile de se familiariser avec le fonctionnement de l’abaque de Smith en faisant glisser un ou plusieurs « Marker » sur le diagramme affiché à l’écran du VNA.
Philip Smith a développé (1939) son « Abaque » ou diagramme de Smith, en premier lieu pour effectuer la transformation entre impédance et coefficient de réflexion, et réciproquement, sans avoir besoin d'une manipulation mathématique de nombres complexes.

Le diagramme de Smith de l’impédance.
La ligne horizontale couvre toutes les impédances purement résistives. Le demi-cercle supérieur du diagramme couvre toutes les impédances complexes inductives Z= R+jLω et le demi-cercle inférieur couvre toutes les impédances complexes capacitives Z= R+(1/jCω).
Les échelles des réactances dans les deux demi-cercles ne sont pas linéaires, elles sont curvilignes et sont normalement dimensionnées en impédances mises à l'échelle par rapport à Z0.
Le point central du graphique est Z0 (50 Ω résistif dans un cas normal), et le cercle extérieur localise toutes les impédances réactives aussi dissemblables qu'il est possible d'obtenir à partir de Z0. L'extrémité gauche de la ligne médiane, où elle rencontre le cercle, est d'impédance nulle, l'extrême droite de la ligne médiane, où elle rencontre le cercle, est d'impédance infinie.
Le centre au sommet du cercle est une impédance purement inductive de magnitude Z0, et le centre du bas est le miroir capacitif du haut.
Le travail remarquable de Philip Smith pour l’époque, a été très utile pendant de nombreuses décennies principalement comme « règle à calcul ». Mais à l’heure du « computer » et du NanoVNA est-il encore indispensable de connaître son maniement de manière précise tout comme celle de son ancêtre « la règle à calcul » à échelle coulissante repliée ?
Cependant, il n’est pas pour autant passé de mode, car son utilisation est toujours prisée lors de l’évaluation de réactances à placer en réseau série-parallèle aux bornes d’une impédance pour obtenir son adaptation à la valeur centrale de référence.
4.3 - Le NanoVNA est à la fois un émetteur et un récepteur.
Il possède deux ports : ch0 et ch1 référencés comme S11 et S21
Il émet par le port Ch0 et reçoit l’onde réfléchie au même port.
Sur l’autre port Ch1 il peut uniquement recevoir.
Il analyse le circuit connecté par la mesure des paramètres « S », S11 et S21 sur une plage de fréquences déterminée du signal émis connu en amplitude et en phase.
Il affiche des grandeurs électriques en amplitude et en phase sous différents formats.
4.4 - Le VNA intègre un Micrologiciel
(Firmware) qui par l’utilisation des paramètres « S » va nous offrir instantanément, sous différents formats, les résultats calculés des différentes grandeurs en relation avec le comportement électrique du circuit sous test.
4.5 - Que pouvons-nous obtenir avec un NanoVNA ?
- Sur une plage de fréquence déterminée :
- Quantifier le rapport de l’amplitude maxima à minima de l’onde stationnaire de tension, le ROS,
- Vérifier le coaxial pour les coupures éventuelles,
- Mesurer l’atténuation de la ligne, du coupleur et du balun sur la plage de fréquences analysée,
- Mesurer la longueur métrique de la ligne,
- Contrôler les courbes de réponse des « Trappes », des circuits d’adaptation « Coupleurs » et Baluns, filtres,...
- Quantifier les composantes résistives et réactives d’impédances, de condensateurs, d’inductances.
- Rechercher la fréquence de résonance de composants individuels comme les fréquences de résonance de l'antenne.
5 - Les paramètres « S »
Les « Scatering Parameters » ou paramètres « S » de diffusion ou de répartition sont une aide extrêmement utile à la conception. Ils sont faciles à comprendre, pratiques et fournissent une multitude d'informations en un coup d'œil.
Les paramètres « S » utilisent les ondes incidentes et réfléchies normalisées à Z0 se propageant à chaque port d’un réseau. Le réseau se termine toujours par l'impédance caractéristique du système de mesure, l’impédance de source ZS en ch0 est égale à l’impédance de charge ZL en ch1 qui est égale à l’impédance caractéristique Z0 de la ligne de transmission.
Dans la plupart des systèmes de mesure, cette impédance est de 50 ohms (purement résistive).
Le NanoVNA est un système de mesure à deux ports et dans une seule direction, (cfr 5.2).
5.1 - Les Paramètres S et le réseau à deux ports et deux directions
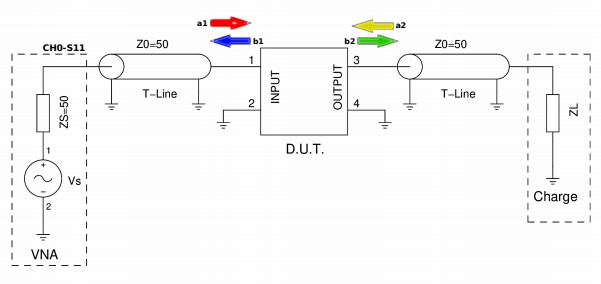
Fig.3 Ondes incidentes et réfléchies dans un dispositif à deux ports et deux directions.
Nous insérons un réseau D.U.T. (Device Under Test) à deux ports entre la source et la charge.
Nous pouvons déduire ce qui suit pour toute onde progressive provenant de la source :
- Une partie de l'onde provenant de la source (a1) et incidente sur le dispositif à deux ports sera réfléchie (b1) et une autre partie sera transmise à travers le dispositif à deux ports.
- Une fraction du signal transmis est alors réfléchie par la charge et devient incidente sur la sortie du dispositif à deux ports (a2).
- Une partie du signal (a2) est ensuite réfléchie (b2) depuis le port de sortie vers la charge, tandis qu'une fraction est transmise à travers le dispositif à deux ports vers la source.
Il est évident d'après l’examen ci-dessus que toute onde progressive présente dans le circuit est constituée de deux composantes.
Par exemple, la composante totale des ondes progressives s'écoulant de la sortie du dispositif à deux ports vers la charge est en fait constituée de b2, la partie de a2 qui est réfléchie par la sortie du DUT, augmentée de la partie de a1 qui est transmise à travers le dispositif à deux ports. De même, l'onde totale de propagation circulant de l'entrée du dispositif à deux ports vers la source est composée de b1, la partie de a1 qui est réfléchie par l’entrée du DUT, augmentée de la fraction de a2 qui est transmise à travers le dispositif à deux ports.
Si nous mettons ces observations sous forme d'équations, nous obtenons ce qui suit :
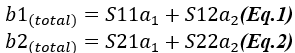
dans lesquelles : S11 = le coefficient de réflexion à l’entrée,
S12 = le coefficient de transmission inverse,
S21 = le coefficient de transmission directe,
S22 = le coefficient de réflexion à la sortie.
Remarque :
Dans (Eq.1), si nous posons a2=0, pas de réflexion par la charge, alors : ![]() (Eq.3)
(Eq.3)
Le rapport de l’onde réfléchie à l’onde incidente, S11, représente par définition le coefficient de réflexion de l’entrée qui peut être tracé sur un diagramme de Smith et l'impédance d'entrée du dispositif à deux ports peut être trouvée immédiatement.
Dans (Eq.2), si nous posons a1=0, alors : ![]() (Eq.4)
(Eq.4)
Il s'agit également d'un coefficient de réflexion, de la sortie, qui peut être tracé sur un graphique de Smith. Ainsi, l'impédance de sortie du DUT à deux ports peut également être trouvée immédiatement.
Les deux autres paramètres S se déduisent comme suit :
Dans (Eq.2), en posant a2=0, pas de réflexion de la charge, on obtient :
Le coefficient de transmission direct ![]() (Eq.5)
(Eq.5)
Dans (Eq .1), en posant a1=0, on obtient :
Le coefficient de transmission inverse ![]() (Eq.6)
(Eq.6)
Notez que ces équations nécessitent que a1 ou a2 soit positionné à zéro pour mesurer les paramètres S individuels. Cela se fait facilement en imposant ZS et ZL à être égaux à l'impédance caractéristique du système de mesure. Par conséquent, toute onde incidente sur ZS ou ZL est totalement absorbée et aucune n'est réfléchie vers le dispositif à deux ports.
5.2 - Le NanoVNA est un système de mesure à deux ports et dans une seule direction.

Fig.4 Configuration de la mesure du S11 et du S21
Prenons l’exemple de la mesure du coefficient de réflexion de l'entrée S11.
Idéalement, nous aimerions fournir un signal d'entrée à l'appareil à deux ports et mesurer uniquement la fraction du signal d'entrée qui est réfléchie vers la source. Dans une situation réelle cependant, une partie du signal incident transmise via le dispositif à deux ports, est réfléchie (a2) par l'impédance de charge, puis retransmise par le dispositif à deux ports vers la source. Le signal réfléchi mesuré est alors un agrégat composé de la partie de a1 qui est réfléchie par l’entrée du DUT et de la partie de a2 qui est transmise en retour.
De toute évidence, ce n'est pas ce dont nous avons besoin.
Cependant quand ZL est réglé égal à Z0, il n'y a pas de réflexion de la part de la charge et le signal réfléchi mesuré depuis le port d'entrée, divisé par le signal incident sur ce port, est véritablement le coefficient de réflexion de l'entrée, S11. Des arguments similaires peuvent être avancés pour les autres paramètres S à mesurer.
Par conséquent, pour mesurer les paramètres S d'un réseau à deux ports, le réseau est toujours terminé (source et charge) dans l'impédance caractéristique du système de mesure ; donc en éliminant toutes les réflexions en provenance des terminaisons.
La signification de S21 et S12, comme indiqué dans les Eq.5 et Eq.6, est qu'ils représentent simplement le gain (ou la perte) direct et inverse du réseau à deux ports, respectivement, lorsque le dispositif à deux ports se termine dans l'impédance caractéristique du système de mesure.
Pour effectuer la mesure du S22 et du S12, il suffit de retourner le D.U.T. dans la configuration schématisée ci-dessus.
6 – La fonction du canal ch0 du NanoVNA
C’est à partir de la mesure S11 que le NanoVNA va calculer toutes les autres grandeurs électriques impactées par le fonctionnement du circuit sous test, antenne, lignes, composants individuels, ...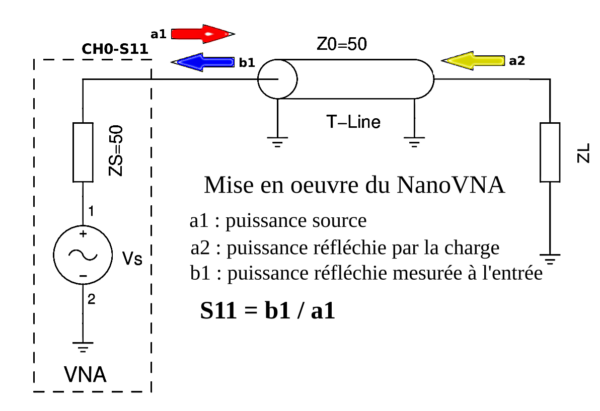
Fig.5 Configuration pour le relevé S11 à partir de ch0
6.1 - La Perte de Retour (Return Loss)
Le Return Loss exprime le rapport en dB de la puissance réfléchie, « en retour », mesurée à l’entrée de la ligne à la puissance émise par la source à cette même entrée.
Rappel : Le logarithme décimal « n » d’un nombre « N » est l‘exposant qu’il faut donner à 10 pour obtenir ce nombre : n=log(N) ou ![]() . Ex :
. Ex : ![]()
Le logarithme du produit [A x B] est égal à la somme des logarithmes de A et B [log A + log B]
Le logarithme de la division [A/B] est égal à la différence des logarithmes de A et B [log A – log B]
Le logarithme de la puissance d’un nombre [AB] est égal au produit du logarithme du nombre par son exposant log [AB] = B log A.B pouvant être entier, fractionnaire, positif ou négatif.
pour =>
=>
Ce paramètre de mesure peut être positif ou négatif, suivant que le rapport de la puissance de sortie à la puissance d’entrée est supérieur à « 1 » ou inférieur à « 1 » c-à-d compris entre 0 et 1.
En transposant cette relation à la tension appliquée et la tension réfléchie au port ch0 du VNA : ![]()
Dans le cas présent, le coefficient de réflexion de puissance à l’entrée ρS2=Pref / Pin comme le coefficient de réflexion en tension ρs = Vref / Vin sera toujours compris entre 0 pour pas de réflexion, et 1 pour la réflexion totale, et le Return Loss sera toujours un nombre négatif.
Cependant chez certains auteurs le Return Loss peut exprimé par un nombre positif, signe « - » devant le logarithme, parce qu’une perte est une quantité positive de perte qui correspond à une quantité négative de gain et réciproquement. Question de sémantique uniquement.
Une perte de retour (dB) élevée est un paramètre de mesure favorable qui est généralement corrélé à une faible perte d'insertion .

En CH0 le S11 ou le Return Loss proche de 0dB indique une réfexion pas loin d’être totale.
En CH1 le S21, la fonction de transfert à travers le circuit sous test montre une atténuation du signal de 33.81dB soit environ 1/2.000.
Exemple :
-20dB représente une puissance réfléchie de 1/100 de la puissance appliquée -20dB=10log(1/100) et une tension réfléchie de 1/10 de la tension appliquée -20 dB = 20 log(1/10).
Ou plus simplement : le rapport des tensions est la racine carrée du rapport des puissances et inversement le rapport des puissances est le rapport des tensions à la puissance 2.
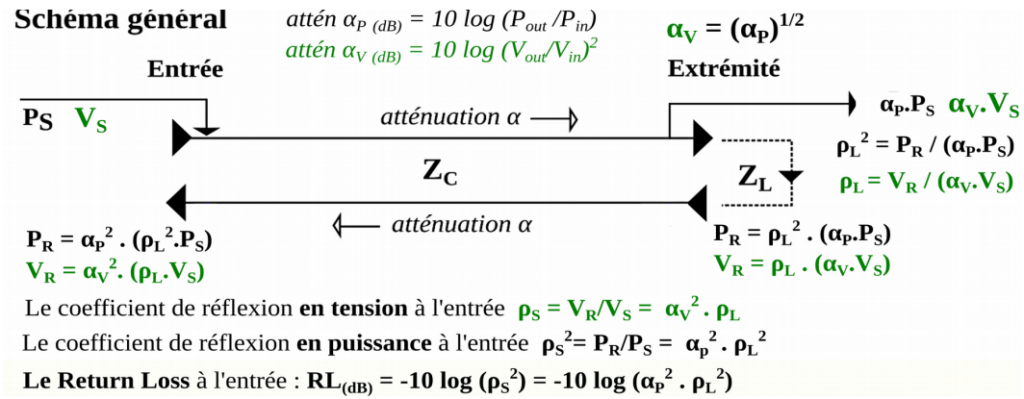
En se référant au schéma ci-dessus, le Return Loss s’exprime aussi comme :
RL(dB) = -10 log (ρS2) ou par son équivalent RL(dB) = -20 log (ρS)
En faisant intervenir le ROS à l’entrée : ![]()
Nous pouvons constater à l’examen du schéma ci-dessus que le coefficient de réflexion en tension ρS à l’entrée n’est autre que le S11 mesuré qui indique l’atténuation apportée par la ligne et ses éventuels accessoires, en plus du coefficient de réflexion apporté par la charge.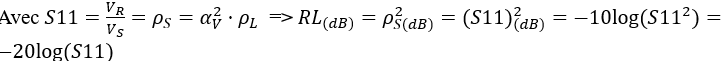
Pour ![]() pas de réflexion à l'entrée.
pas de réflexion à l'entrée.
Pour ![]() atténuation de la ligne.
atténuation de la ligne.
Le Return Loss permet des mesures plus précises pour des faibles valeurs de puissance réfléchie Exemple :
un ROS = 1.5:1 => ![]()
un ROS = 1.2:1 => ![]()
Déduire la valeur du Return loss à partir d’une lecture d’un ROS mètre est plus qu’imprécis, sachant que l’échelle de lecture de l’appareil manque généralement de la finesse appropriée.
7- Comprendre les grandeurs électriques calculées et les relations qui les lient.
Remarque : L’indice (L) est utilisé dans les équations suivantes pour spécifier qu’elles se rapportent à des valeurs déterminées à la charge (Load). Car en chaque point de la ligne de transmission, la valeur du ROS et de ρ varie principalement en fonction de l’atténuation de la ligne et donc de la distance par rapport à la charge. (voir également le BA-BA de la Ligne de transmission)
7.1 - Le Rapport de l’Onde Stationnaire de tension (R.O.S)
Est une quantité qui indique à quel point l'impédance de l'antenne est adaptée à l'impédance de la ligne qui la relie à l’émetteur. Une valeur inférieure à 1.5:1 est souhaitable. Un SWR faible, uniforme sur la largeur de bande souhaitée, permet un transfert maximal de puissance de la ligne de transmission à l’antenne.
Le ROS est défini comme le rapport entre la tension maximale et la tension minimale de l’onde stationnaire de tension le long de la ligne de transmission. ![]() (Eq.7)
(Eq.7)
dans laquelle :
Vinc est le tension incidente à la charge
Vref est la tension réfléchie par la charge
La valeur du ROS, est déterminée par le rapport des impédances de la charge ZL et de la ligne Z0 en présence à la jonction antenne-ligne de transmission. ![]() (Eq.8)
(Eq.8)
avec :|ZL| = la valeur absolue de l’impédance d’entrée de l’antenne sous la forme ![]()
|Z0| = l’impédance caractéristique de la ligne le plus souvent sous la forme ![]()
7.2 - Le coefficient de réflexion de tension « ρL » à la jonction antenne
se calcule comme :![]() (Eq.9). En substituant Eq.9 dans Eq.7 :
(Eq.9). En substituant Eq.9 dans Eq.7 :![]() (Eq.10)
(Eq.10)
qui par transformation donne : ![]() (Eq.11)
(Eq.11)
ρL à l’antenne est fonction de l'impédance de charge, ZL, et de l'impédance caractéristique Z0 de la ligne.![]() (Eq.12) La substitution de Eq.11 dans l’Eq.10 nous ramène à l’Eq.8
(Eq.12) La substitution de Eq.11 dans l’Eq.10 nous ramène à l’Eq.8
7.3 - Le coefficient de réflexion de puissance « ρL2 » à la jonction antenne
se calcule comme : ![]() (Eq.13)
(Eq.13)
Une adaptation d’impédance parfaite est obtenue lorsque ZL= Z0, qui dans (Eq.8) donne SWR=1 et dans (Eq.11) ρL=0 .
Lorsque l'impédance caractéristique de la ligne et l'impédance d’entrée de l'antenne ne correspondent pas, ![]() alors la ligne d’alimentation devient le siège d’une onde stationnaire à la fois en tension et en courant. Elle se comporte alors, sur toute sa longueur, comme un transformateur variable de l’impédance de l’antenne, vers une impédance complexe
alors la ligne d’alimentation devient le siège d’une onde stationnaire à la fois en tension et en courant. Elle se comporte alors, sur toute sa longueur, comme un transformateur variable de l’impédance de l’antenne, vers une impédance complexe ![]() à son entrée qui est fonction de la fréquence utilisée, plus précisément de sa longueur d’onde, et ainsi de la longueur « électrique » de la ligne. (Voir Annexe 1 et Annexe 2)
à son entrée qui est fonction de la fréquence utilisée, plus précisément de sa longueur d’onde, et ainsi de la longueur « électrique » de la ligne. (Voir Annexe 1 et Annexe 2)
Même si une adaptation est réalisée à l’émetteur à l'aide d'un réseau d'adaptation, coupleur d’antenne, le ROS ne changera pas entre le coupleur et l’antenne, mais la longueur de la ligne alimentant l'antenne reste importante pour son rôle de transformation de l’impédance de l’antenne.
 |
Exemple des paramètres calculés par le NanoVNA et donnés dans le logiciel NanoVNAsaver, pour une antenne mobile ( pas très bien installée sur un plan de masse). |
7.4 - Perte d’insertion de la ligne de transmission
Toute ligne de transmission réelle présente une « perte d’insertion » plus ou moins importante en fonction de sa construction et de la fréquence utilisée. Le fabricant fournit généralement cette perte sous forme d’une atténuation exprimée en dB pour une longueur donnée de ligne, généralement 100 pieds ou 30 mètres. Cette perte appelée « Perte à l’adaptation » ou « Matched Line Loss (MLL) » est celle d’une ligne adaptée où l’impédance de charge est égale à l’impédance caractéristique de la ligne.
Cependant lors de son utilisation, la ligne peut présenter des pertes supplémentaires, pertes dans les connecteurs, humidité dans ou sur la ligne, et notamment lorsqu’un ROS important est présent sur la ligne (cfr B.A.-BA seconde partie).
7.5 - Perte d’insertion(dB) comparée au coefficient d’atténuation de puissance ou de tension.
Nous savons tous approximativement quelle puissance notre émetteur délivre lorsqu'il alimente une charge de 50 Ω.
Cependant nous désirons connaître quelle est la quantité de cette puissance qui est absorbée ou rayonnée par la ligne de transmission comme dans les éventuels coupleur et balun et donc la puissance qui ne « profite » pas à l'antenne et réciproquement quelle est le coefficient d’atténuation apporté par le circuit.
Prenons l’exemple d’un émetteur qui délivre 100 W HF à l’entrée du circuit qui alimente l’antenne dont seulement 80 W HF sont disponible à la sortie ZL. Le circuit présente une quantité nette de puissance perdue de 20 W HF.
Si l’on désire généraliser cette « quantité perdue » pour n’importe quelle puissance à l’entrée, il y a lieu de passer par le coefficient d’atténuation, le rapport de la puissance à la sortie à la puissance d’entrée, qui dans le cas présent est 80W/100W = 8/10.
Dans un second temps, si nous appliquons en lieu et place une puissance de 50 W HF à l’entrée du circuit, le coefficient d’atténuation de 8/10 déterminé ci-avant s’applique encore, car il est lié aux propriétés électriques du circuit et non à la puissance appliquée à l’entrée. On obtient donc une puissance disponible en sortie 50 W x 8/10 = 40 W HF. La quantité nette de puissance perdue dans le circuit est ici de 10 W HF.
Si la quantité nette de puissance perdue change en fonction de la puissance à l’entrée, le coefficient d’atténuation reste inchangé
Le coefficient d’atténuation de 8/10 donne :![]()
Pour la puissance d’entrée de 100 W = 20 dB<suB<(W), la puissance à la sortie sera :
Puissance (dB) - l’atténuation (dB) = 20 dB(W) – 0.97dB = 19,03 dB(W) =>P(sortie) = 10 19,03/10 = 80W.
La « Perte » de 0.97 dB ne représente donc pas les 20 W « perdus» dans la traversée de la ligne.
Pour la puissance d’entrée de 50 W = 17 dB(W) la puissance à la sortie sera :
Puissance (dB) - l’atténuation (dB) = 17 dB(W) – 0.97dB = 16,03 dB(W)=> P(sortie) = 10 16,03/10 = 40 W.
Nous pouvons constater ici que 0,97dB représente deux quantités différentes en fonction de la puissance d’entrée s’il est considéré comme une « quantité » perdue et non comme un coefficient d’atténuation.
Les données de « Perte(dB) d’insertion » ou « Atténuation(dB) » fournies par le fabricant d’une ligne de transmission, qui sont les pertes quand la ligne est adaptée, nécessitent une translation mentale d’une « perte » logarithmique exprimée en dB en son coefficient d’atténuation linéaire. Certaines de ces translations sont bien connues : -3 dB ~ (1/2) ; -6dB ~ (1/4) ; -9dB ~ (1/8) et dans les faibles valeurs -2 dB ~ (6/10) ; -1.5 dB ~ (7/10) ; -1 dB ~ (8/10) ; 0dB = (1).
Résumé : la notion de « Perte(dB)» est à comprendre comme coefficient appliqué à la puissance d’entrée.
8 – Exemples de Mesures
8.1 – La perte d’insertion de la ligne à l’adaptation
Remarque : concerne la perte de la longueur de la ligne sous test et non la perte par 100 pieds.

Le schéma précédent peut être adapté pour que le Return Loss exprime en dB uniquement le coefficient d’atténuation α2 du câble, à la fréquence sélectionnée, en forçant ρL2 =1, au moyen d’une extrémité ouverte ou en court-circuit.
Lorsqu’un court-circuit d’extrémité est utilisé, les courants sur la tresse et le conducteur central sont plus élevés que dans le cas d’une ligne adaptée. Cela conduit à une perte accrue (RI2).
La perte dans le cuivre est proportionnelle au carré du courant et est supérieure à la perte dans le diélectrique.
Pour une ligne ouverte à son extrémité, le courant dans le coaxial est plus faible que dans le cas d’une ligne adaptée. Ce qui conduit à une perte plus faible.
L’extrémité ouverte et en court-circuit donneront des valeurs RLSC et RLOC différentes d’autant plus que la longueur de la ligne est petite.
La détermination fiable des valeurs RLSC et RLOC par un simple relevé des ROSSC et ROSOC au moyen d’un ROS-mètre est à la limite illusoire au vu des valeurs très élevées du ROS dans ces conditions extrêmes de désadaptation.
La réflexion est totale, le coefficient de réflexion est proche de 1 et le ROS théoriquement « infini ».
Face à ces valeurs infinies du ROS il est possible de recourir aux valeurs du Return Loss, (0,01dB <=> 0,005 dB) pour c’est deux configurations.
La question qui se pose alors est de savoir à laquelle des deux faire confiance pour obtenir la perte d’insertion à l’adaptation sachant que les mesures ont été effectuées dans des conditions de désadaptation totale
Une solution a été proposée par F. Witt (QEX may /june 2005), qui choisit d’utiliser la moyenne géométrique des coefficients de réflexion à l’entrée : ![]() (Eq.14)
(Eq.14)
avec : ρ(SC) = α(SC) et ρ(OC) = α(OC)
L’atténuation moyenne αm : ![]() et
et ![]() (Eq.15)
(Eq.15)
calculés à partir des RLShort et RLOpen mesurés à l’entrée soit : ![]()
la Perte à l’adaptation devient : ![]() (Eq.16)
(Eq.16)
Pourquoi prendre la moyenne géométrique ![]()
L’exemple de la méthode indirecte, (voir 8.3) , va nous éclairer sur le sujet.
Exemple : Pour un court-circuit ou un circuit ouvert en sortie : ρL =1 10log(1)=0dB
Un SWR 2:1 à l’entrée de la ligne 
Pour 100 W à l’entrée : ![]()
Le RL représente le coefficient d’atténuation de la puissance d’entrée et RL(dB) représente la perte d’insertion pour le trajet aller + retour de la puissance d’entrée sur la ligne.
Pour un trajet simple, la perte d’insertion de la ligne est : ![]()
La puissance à l’extrémité charge est : 20dB-4,77dB=15,23dB=33,34W pour 100W à l’entrée.
ou ![]()
8.2 - Perte coaxiale calculée directement en termes d'impédance
La mesure de la perte coaxiale α=ρS (voir schéma équivalent) peut être calculée en décibels comme :![]() (Eq.17)
(Eq.17)
dans laquelle Zoc représente l'impédance d'entrée lorsque la ligne se termine par un circuit ouvert, et Z0 est l'impédance caractéristique de la ligne de transmission. D’un autre côté, lorsque la ligne se termine par un court-circuit, l'impédance d'entrée ZSC doit être utilisée à la place de Zoc dans l’(Eq.17). Cette équation est implémentée dans le logiciel de plusieurs analyseurs d'antennes et analyseurs de réseaux vectoriels (VNA).
L’utilisation de (Eq.17), ne nécessite qu’une seule mesure d'impédance, étant donné la valeur nominale 50 Ω spécifiée par le fabricant pour Z0. Cependant l’application de cette équation avec ZOC et ZSC mesurés peut donner des valeurs de perte très différentes. Une explication à cela (Frank Witt) est que la valeur nominale de 50 Ω utilisée pour Z0 n’est pas la valeur correcte. Le coaxial avec perte du monde réel a une impédance caractéristique à valeur complexe dépendant de la fréquence. Dans (Eq.17), l’approximation à un nombre constant réel pour Z0 peut être justifiée si la perte coaxiale est suffisamment petite.
Et si nous reprenons la moyenne géométrique des coefficients de réflexion (Eq.14) : ![]() avec
avec ![]() et
et![]()
Les deux amplitudes du coefficient de réflexion sont calculées en utilisant une valeur nominale Z0 spécifiée par le fabricant, parfois programmée dans l'instrument de mesure. Comme mentionné ci-avant, l'impédance caractéristique réelle du coaxial peut être significativement différente de la valeur nominale Z0 en plus de la détérioration et de la contamination par l'humidité du diélectrique du coaxial par exemple, et cela peut entraîner des erreurs lors de l'utilisation de (Eq.17). Même si ces erreurs ne sont pas significatives, le processus de calcul de la perte coaxiale devrait bénéficier d'une formule plus simple que (Eq.17).
Dans ce qui suit, une formule de perte est décrite qui ne contient pas explicitement Z0 ou ne nécessite pas le calcul des coefficients de réflexion.
Une approche plus simple et plus attrayante consiste à :
1) empêcher Z0 d'apparaître explicitement dans la formule de la perte, et
2) ne pas nécessiter le calcul des coefficients de réflexion.
Remplacez Z0 dans (Eq.17) par ![]() qui est une formule correcte pour l'impédance caractéristique, pour obtenir :
qui est une formule correcte pour l'impédance caractéristique, pour obtenir : 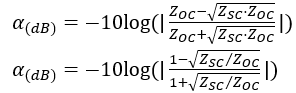
Cette équation plus simple nécessite la mesure et l'utilisation des valeurs complexes de Zoc et Zsc. Elle ne contient pas explicitement Z0 ni ne nécessite le calcul des coefficients de réflexion.
Remarquez la racine carrée Zsc/Zoc comme valeur complexe.
8.3 - Mesure de l’atténuation de la ligne par la méthode indirecte
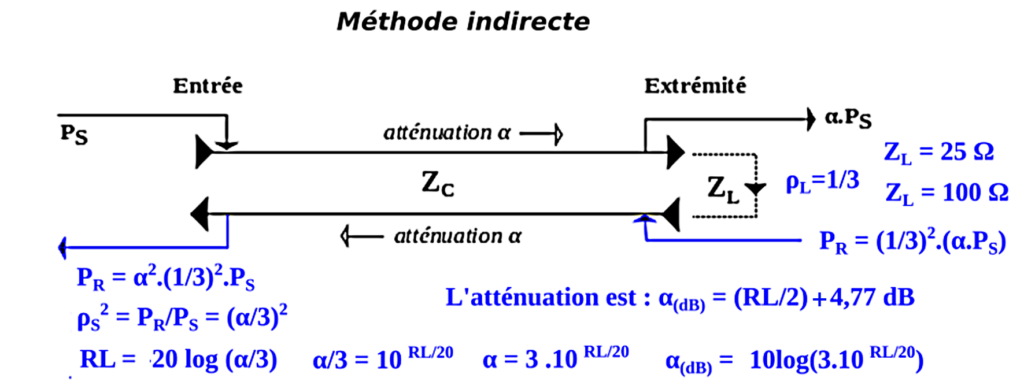
Il est possible de se prémunir des coefficients de réflexion élevés d’une charge en circuit ouvert ou en court-circuit en choisissant deux charges différentes pour le relevé du Return Loss, dont l’une est égale à la moitié de l’impédance caractéristique de la ligne et la seconde est égale à deux fois l’impédance caractéristique. Ainsi pour une ligne d’impédance caractéristique de 50 Ω :
A partir de ![]()
pour la charge de 100 Ω donne :![]()
pour la charge de 25 Ω donne : ![]()

Exemple : La charge adaptée est de 50 Ω pour une impédance caractéristique de 50 Ω. En effectuant une mesure de l’atténuation «α» de part et d’autre de 50 Ω par exemple à 25 Ω et à 100 Ω, la moyenne arithmétique de ces deux impédances est ![]() tandis que la moyenne géométrique de ces deux impédances est de
tandis que la moyenne géométrique de ces deux impédances est de ![]()
C’est la raison pour laquelle la valeur de l’atténuation à l’adaptation 50Ω doit se calculer comme : ![]()
Remarque : ici RL sont des valeurs négatives. L’expression en dB d’un rapport plus petit que « 1 » qui donnera une valeur négative pour α(50)dB, c’est une atténuation.
8.4 – Mesurer la perte d’insertion d'un tuner d'antenne.
- Connectez le NanoVNA à l'entrée du tuner et la résistance à adapter RL à sa sortie.
Remarque : Nous utilisons ici comme charge une résistance de manière à visualiser la perte du Tuner sur la plage de fréquence programmée dans le NanoVNA.
- Ajustez le tuner pour que l'impédance d'entrée du tuner soit 50+j0 Ω (|ρ| = 0, et SWR = 1).
- Sans toucher aux réglages du Tuner,
- Remplacez RL à la sortie du tuner par RL/2 qui impose ![]()
- Relevez les valeurs RL1 du Return Loss fournies par le NanoVNA.
- Remplacez à la sortie RL/2 par 2RL qui impose ![]()
- Relevez les valeurs RL2 du Return Loss fournies par le NanoVNA
- Appliquer : ![]()
9 - La fonction du canal ch1 du NanoVNA
Le canal ch1 est la partie réceptrice du NanoVNA qui permet la mesure de la fonction de transfert S21 du dispositif sous test. La configuration de test est reprise à la Fig.4.
Le DUT est inséré en série entre ch0 et ch1, ce qui permet de relever le gain, l’atténuation, ainsi que la bande passante du DUT qui peut être n’importe quel circuit à une entrée et une sortie comme les circuits accordés de tout type, les trappes, l’impédance de blocage d’un choke balun, les atténuateurs, … et même les lignes de transmission.
Un exercice intéressant serait de comparer l’atténuation de la ligne de transmission à extrémité ouverte ou en court-circuit calculée par la mesure du S11, avec celle relevée par S21 si les deux extrémités peuvent être connectées au Nano.
10 – Mise en œuvre du NanoVNA
Mesurer avec précision la valeur réelle de circuits peut être une tâche assez compliquée, car il y a toutes sortes de phénomènes parasites qui se produisent à chaque fois que vous avez deux conducteurs qui sont proches l'un de l'autre avec une sorte de matériau isolant entre les deux, comme l'air ou le plastique. Vous obtenez de cette façon la capacité parasite d’un condensateur. De plus chaque fil est une inductance quelle que soit sa section et sa longueur.
Nous devons donc trouver un moyen pour connecter le composant à l'instrument de mesure.
Chaque connexion présente une résistance, une capacité et une inductance associée, aussi petite soit-elle.
Selon la théorie des lignes de transmission, l'impédance trouvée à une extrémité d'un morceau de câble coaxial n'est pas nécessairement la même que celle présente à l'autre extrémité du morceau de câble coaxial. Cela dépend de la fréquence utilisée, et des caractéristiques physiques, et électriques du câble coaxial.
Ainsi, tout ce que nous plaçons entre l'instrument de mesure et le dispositif à mesurer, impédance complexe, condensateur ou inductance entraînera une erreur de mesure à un degré ou à un autre.
Comment prendre en compte tous ces éléments parasites afin que la valeur que nous mesurons soit celle réellement présente ?
La première étape que nous devons suivre pour effectuer des mesures précises est l'étalonnage.
10.1 L’étalonnage
Une fois dans la procédure d'étalonnage le NanoVNA mesure tout ce qui peut se trouver entre le VNA lui-même et le dispositif à mesurer. Cela inclut tous les éléments parasites.
Après quoi lorsque nous effectuons la mesure réelle, il prend en considération tous ces éléments parasites et fournit une valeur réelle pour le dispositif sous test.
L'étalonnage de tous les NanoVNA est basé sur la méthode classique (S.O.L.T.) Short, Open, Load, Thru créant un tableau effectif des coefficients d'erreur complexes appliqués point par point systématiquement aux signaux mesurés. Cette procédure est intégrée au micrologiciel du NanoVNA, qui est le cœur du fonctionnement des appareils.
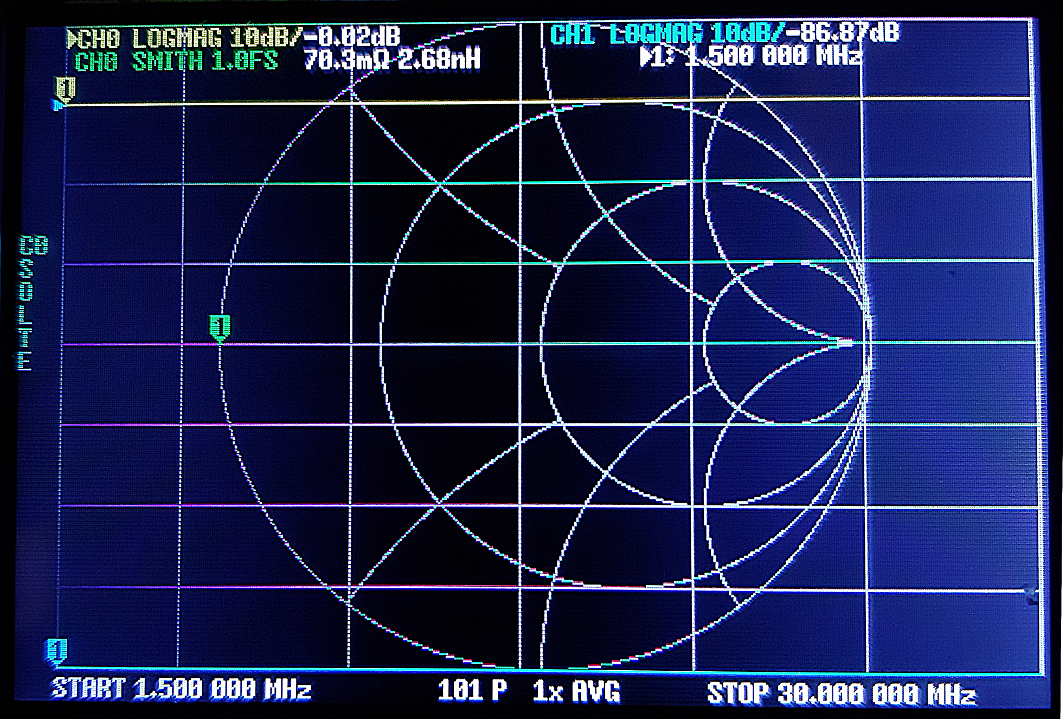 |
SHORT La méthode d'étalonnage SOLT est la technique d'amélioration de la précision la plus courante car elle est naturellement à large bande en raison du fait que la différence de phase de la réflexion entre le standard en court-circuit (Short) et en circuit ouvert (Open) est, en principe, de 180° indépendamment de la fréquence. |
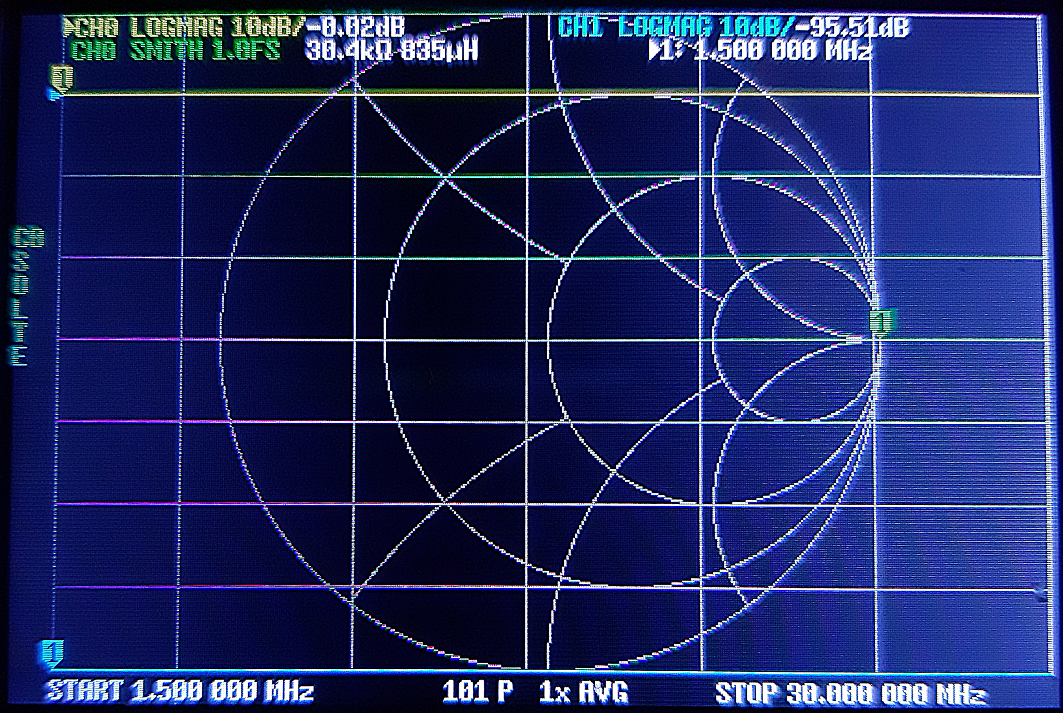 |
OPEN Tous les NanoVNA, étant des dispositifs à 2 ports à chemin dans un seul sens ; l'étalonnage SOLT ne caractérise pleinement que ch0, fournissant idéalement une mesure S11 précise. Cependant, comme il n'y a pas de possibilité d'inversion de sens, le coefficient de réflexion de ch1 n'est pas entièrement pris en compte. |
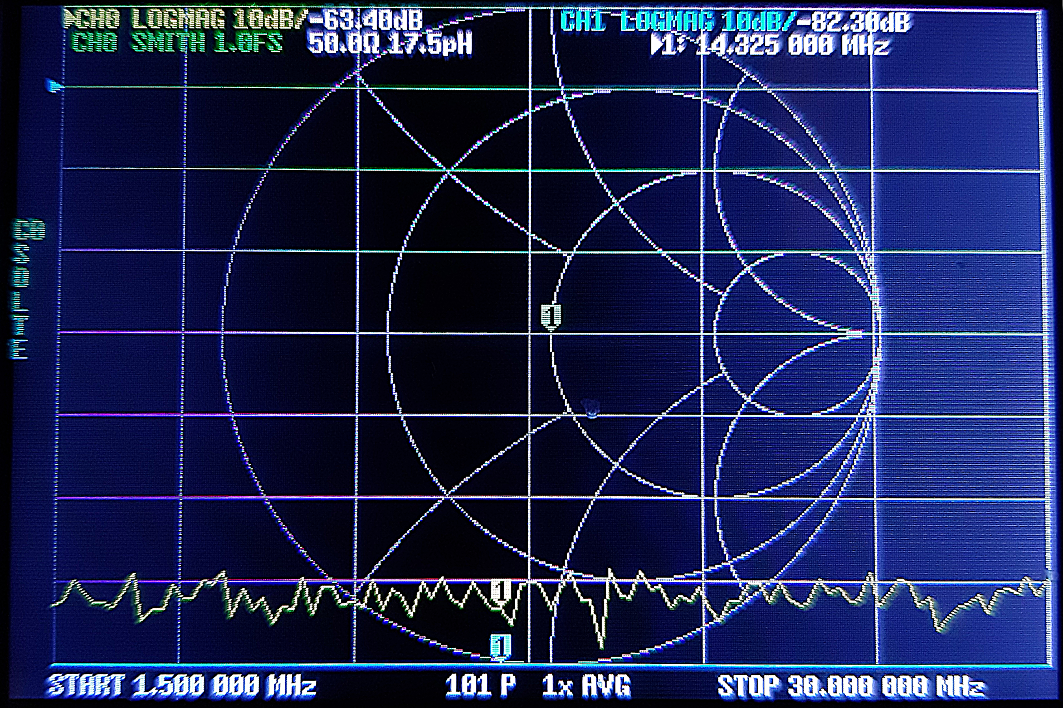 |
LOAD 50 Ohms Ce schéma d'étalonnage fournit un moyen simple et économique de mesurer les deux paramètres directs complexes « S », S11 et S21, avec des limitations en particulier en ce qui concerne les faibles pertes d'insertion. |
10.2 Le Plan de Référence
Nous devons maintenant réfléchir à la manière dont nous allons étalonner le NanoVNA afin de pouvoir effectuer cette mesure aussi précisément que possible.
Pour une meilleure précision, nous devons étalonner le VNA aussi près que possible de l'endroit où l'élément à mesurer sera connecté.
Le Plan de référence est l’élément de terminologie important que vous entendrez souvent dans le monde du VNA.
Il situe l'interface physique entre le VNA et l’endroit où l’on positionne les standards d’étalonnage pour ensuite y placer le dispositif à mesurer.
Le plan de référence est constitué par les faces des connecteurs d’accouplement où se connectent les calibres d’étalonnage.
10.3 Comment et où calibrer le VNA ?
Cela dépend entièrement des calibres d'étalonnage que vous possédez et du type de connecteur dont dispose le composant à mesurer.
Alors que faire si vous possédez seulement les étalons SMA livrés avec l’appareil et que vous devez ajouter un adaptateur pour accueillir l'élément à tester ?
Aussi longtemps que les câbles et les adaptateurs sont tous dans la catégorie 50 ohms, nous pouvons utiliser ce qu'on appelle une extension de port pour déplacer le plan de référence du port du VNA où nous avons effectué l'étalonnage, vers le plan de référence de l'adaptateur.
L'extension de port permet de corriger la longueur du câble après l'étalonnage.
 |
Cette méthode ne fonctionnera pas avec un adaptateur à pinces crocodiles fixées aux bornes d’un connecteur PL ou N, ou d’un adaptateur BNC-connecteur à vis ou BNC-fiches bananes car ces configurations ne sont pas des dispositifs 50 ohms. Nous devons donc étalonner le VNA avec des calibres de confection personnelle connectés aux extrémités de ces adaptateurs hybrides. |
11. NanoVNAsaver
Pour une utilisation en laboratoire/shack, le logiciel gratuit NanoVNAsaver, peut être utilisé pour alimenter le Nano via son interface USB intégrée. Il est nécessaire de connaître cette approche car c'est la manière habituelle de mettre à jour le micrologiciel de l'appareil, de dépasser la résolution de balayage de fréquence limitée à 101 points et de recharger la batterie lithium-ion 3,6 V embarquée.
Relevé des paramètres d’un Balun de courant de 12 tours sur un tore FT43 de1,5MHz à 30MHz
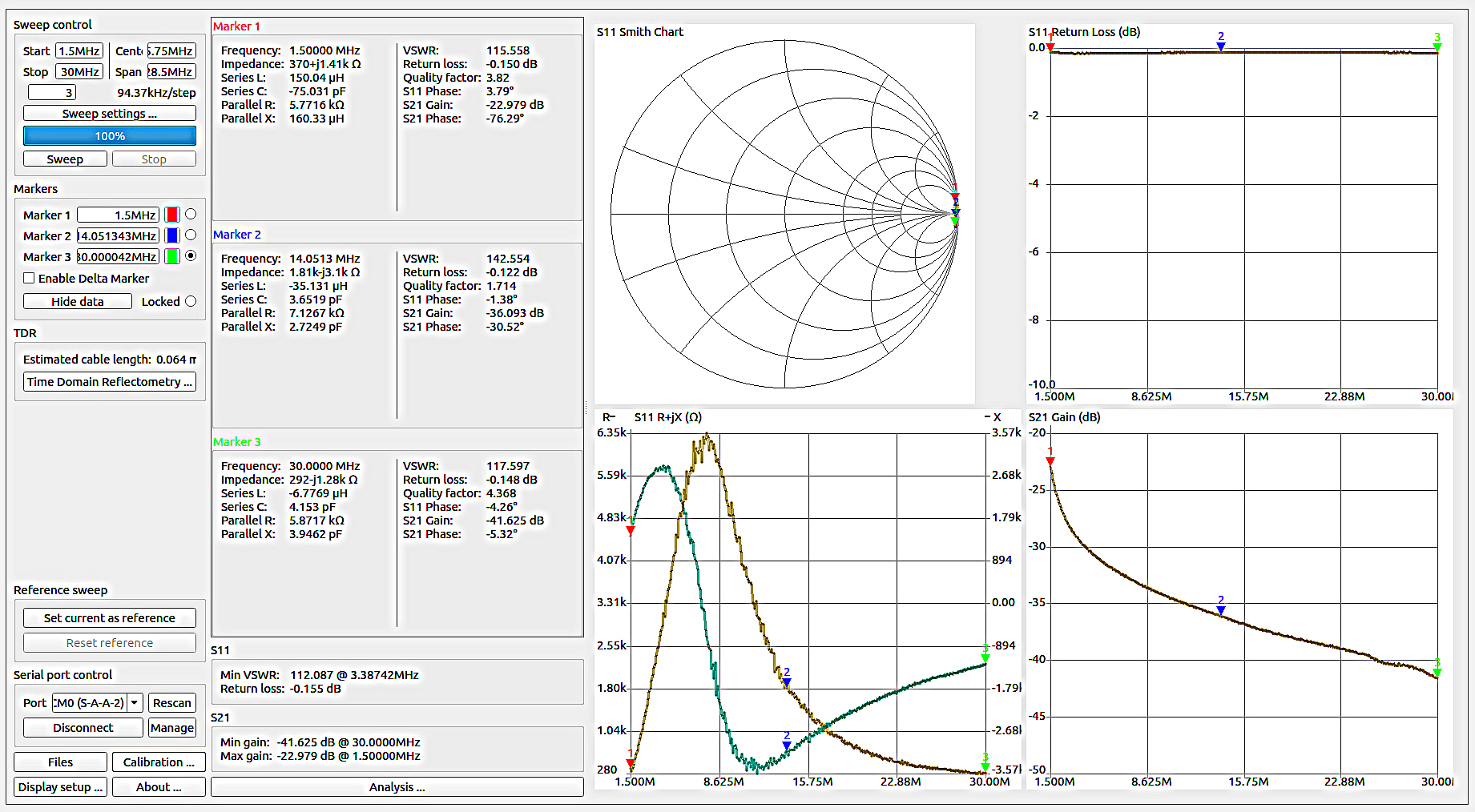
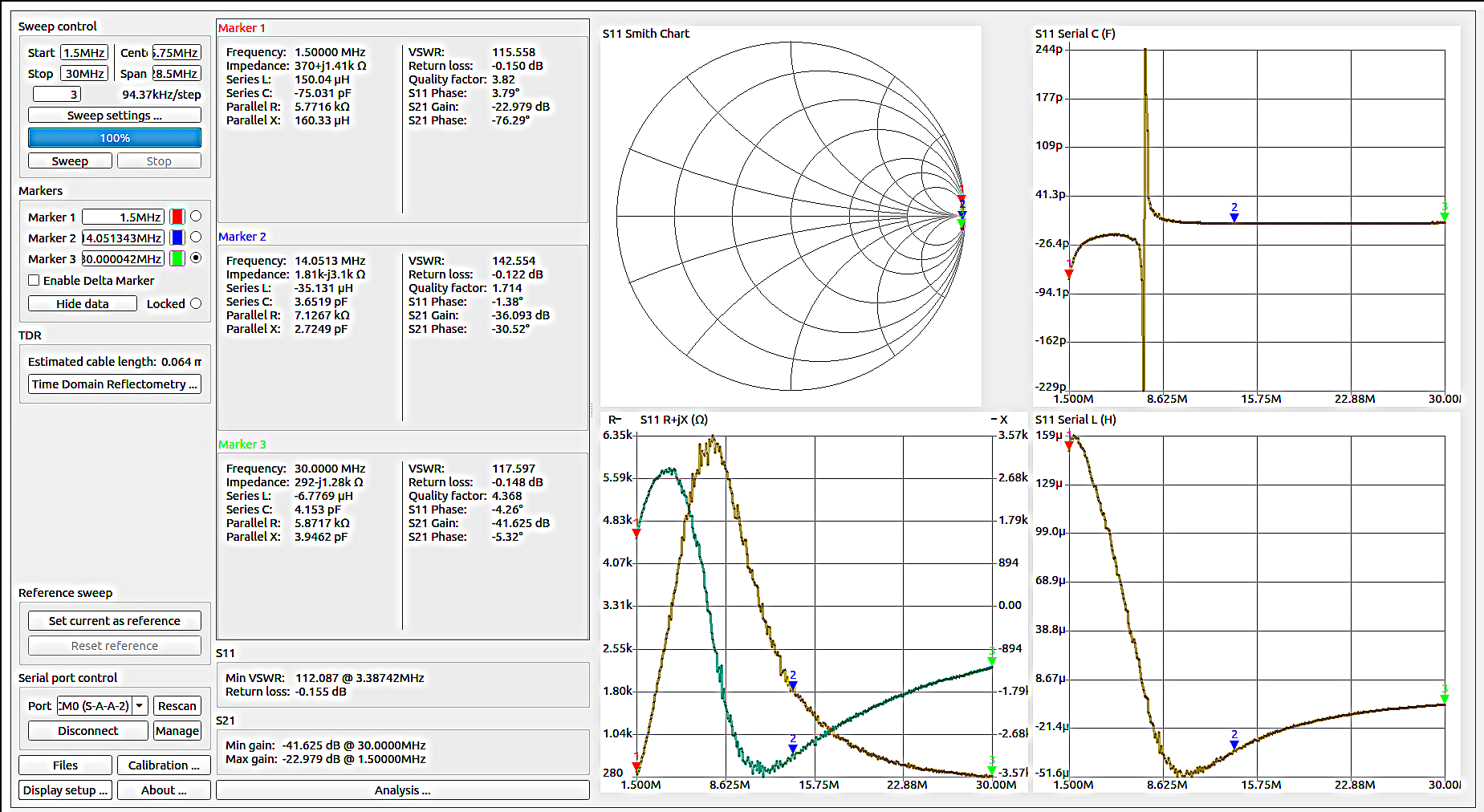
Relevés de l’écran du NanoVNA et du NanoVNAsaver pour une antenne mobile 144-146 MHz
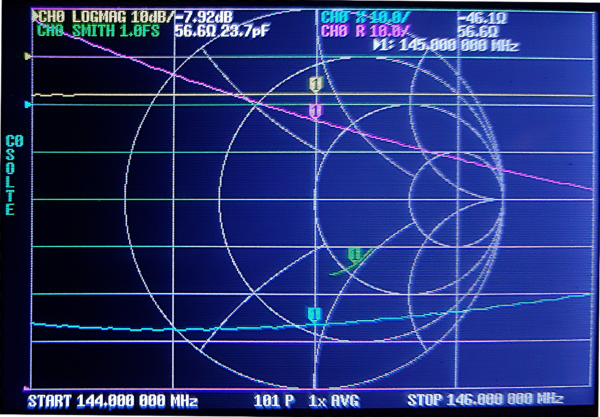

Electriquement, il est facile de constater que le SWR à lui seul ne signifie rien ou presque.
12. Résumé
Comme le titre l’indique, le présent article à pour objectif de faire comprendre le fonctionnement interne du NanoVNA. Ce qu’il mesure effectivement et les paramètres qu’il calcule d’après cette mesure, ainsi que la signification aussi précise que possible de ces paramètres et leurs relations.
Ce n’est donc pas pour l’essentiel un mode d’emploi.
Et dans ce sens il serait susceptible d’intéresser plus spécifiquement le radio amateur que le radio opérateur.
13. Annexe 1 et 2
Annexe 1
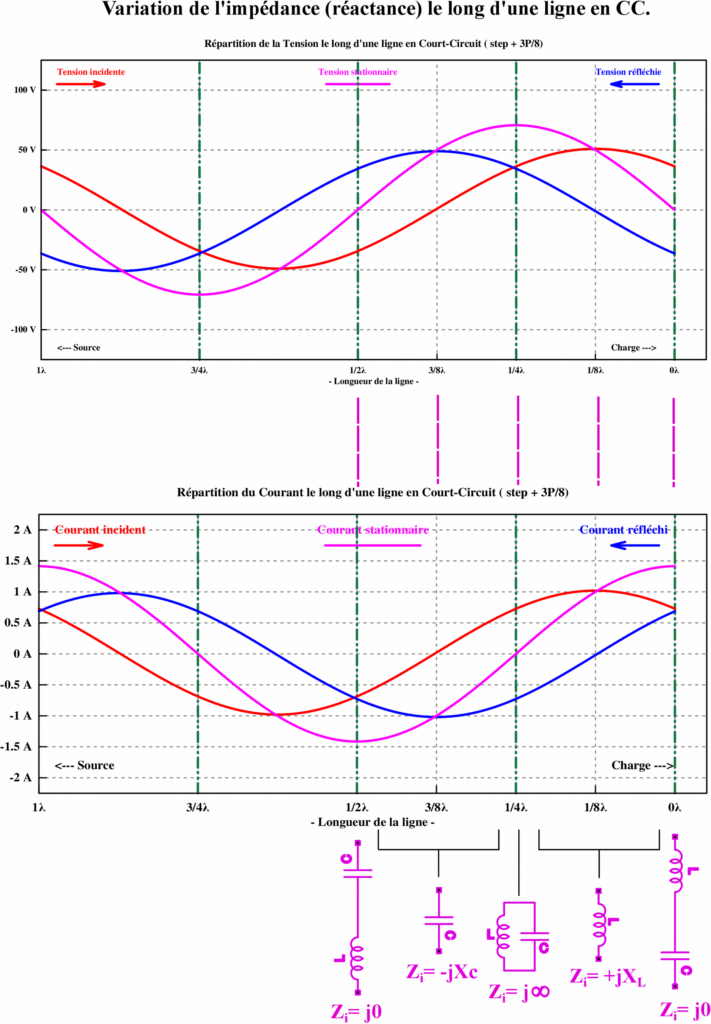
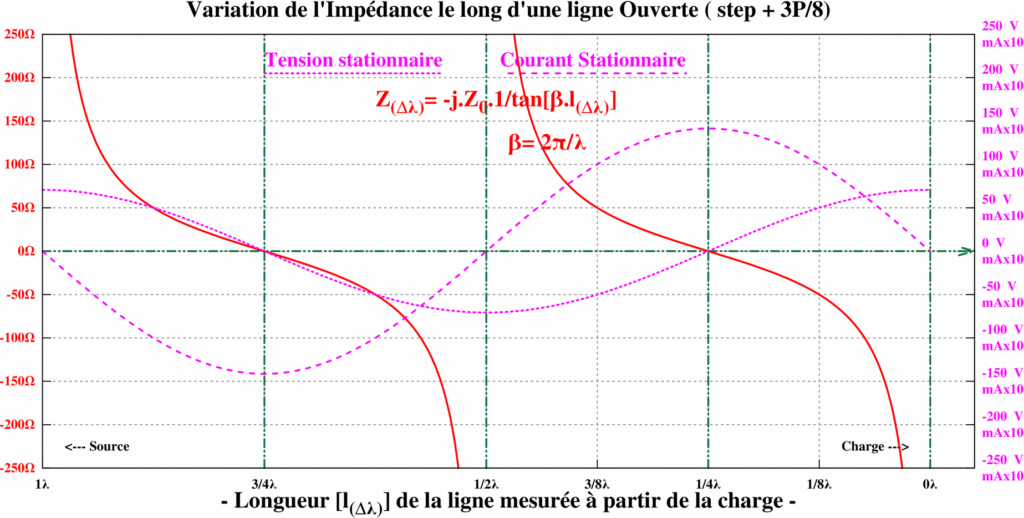
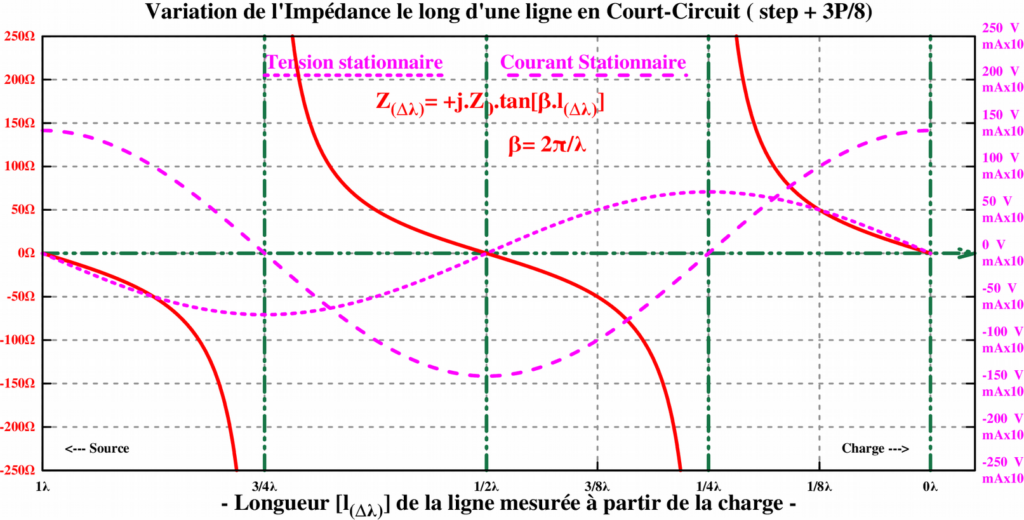
Analyse de la nature de l'impédance vue à l'entrée Zi de la ligne en fonction de la distance comptée à partir de son extrémité (ZL = 0 ou plus généralement ZL ZC)
À l’extrémité « charge » la tension réfléchie est en opposition de phase (180°) avec la tension incidente, la tension résultante (stationnaire) est la différence des deux amplitudes.
À cette même extrémité « charge » le courant réfléchi est en phase (0°) avec le courant incident, le courant résultant (stationnaire) est la somme des deux amplitudes.
La relation de phase de 0° et 180° entre signal réfléchi et incident ne s’applique que dans le cas où la charge est purement résistive.
L’impédance en chaque point de la ligne n’est autre que le rapport en amplitude et en phase de la tension résultante au courant résultant (stationnaire) en ce point Z =V / I
Nous pouvons donc déduire en chaque point de la ligne, le type d'impédance, résistance et/ou réactance rencontré avec son signe et le circuit électrique équivalent.
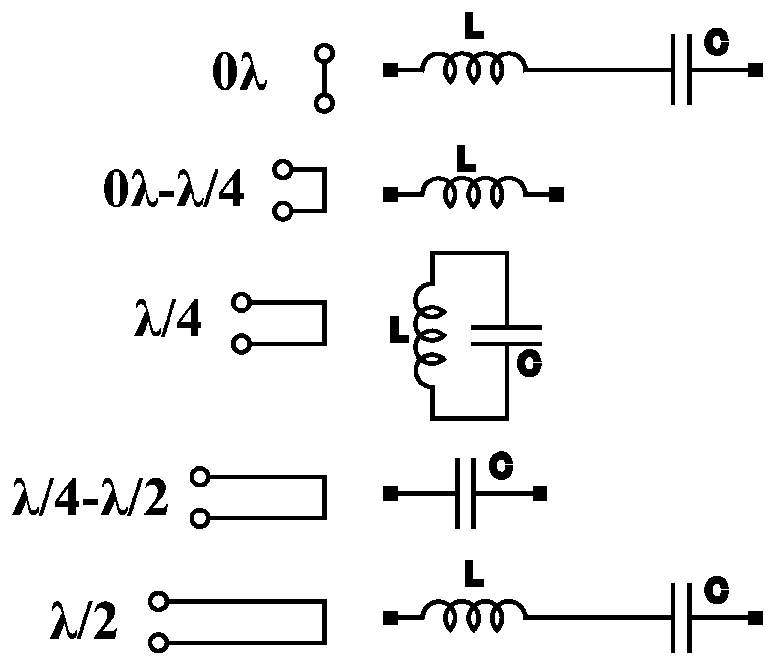
- à l'extrémité 0 λ : le courant est maximum et la tension est minimum, suivant la loi d'ohm Z = 0/I = 0 l'impédance est minimum, ce qui pourrait correspondre au comportement d'un circuit résonnant série. On peut donc l’assimiler à un circuit résonnant série.
- entre 0 λ à λ/4 : le courant augmente et la tension diminue, ce qui correspond à la charge d'une bobine d'induction, le courant est en retard sur la tension, on est en présence d'une réactance inductive Z = + j XL
- à λ/4 : le courant est minimum et la tension est maximum, l'impédance est infinie Z = V /0 = ∞ ce qui correspond au comportement d'un circuit résonnant parallèle, on peut donc l’assimiler à un circuit résonnant parallèle.
- entre λ/4 et λ/2 : la tension augmente et le courant diminue, ce qui correspond à la charge d'un condensateur, la tension est en retard sur le courant, on est en présence d’une réactance capacitive Z = − j XC
- à λ/2 : le courant est maximum et la tension est minimum, l'impédance résultante est minimum, on retrouve le circuit résonnant série comme à l'extrémité, mais avec une inversion de phase. On situe un circuit résonnant série.
Annexe 2
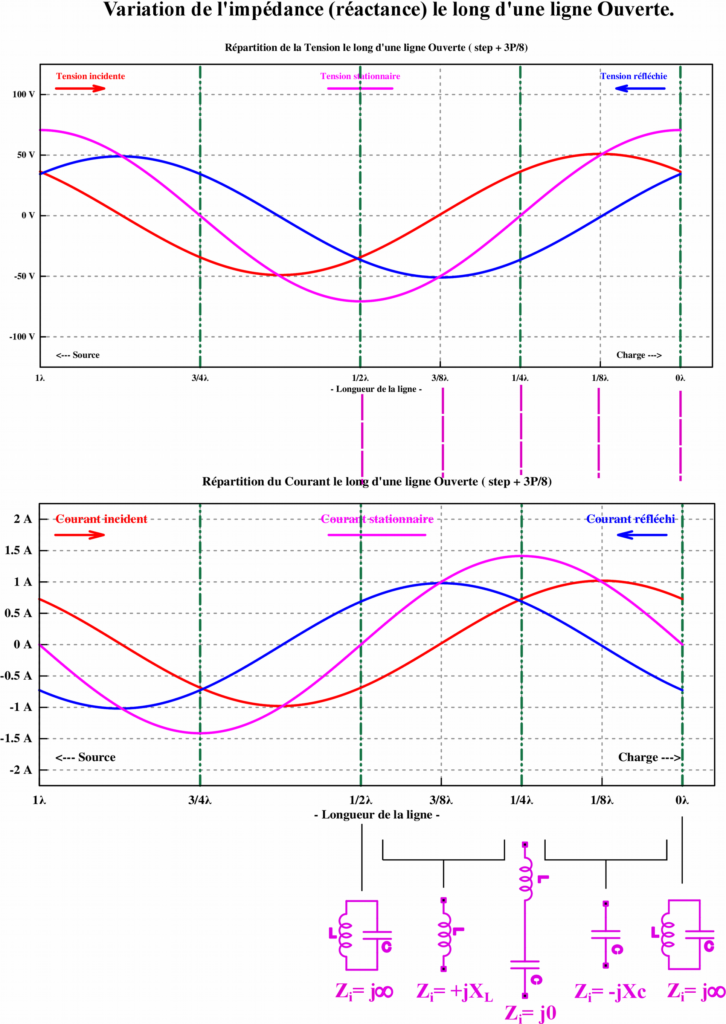
Analyse de la nature de l'impédance vue à l'entrée Zide la ligne en fonction de la distance mesurée à partir de son extrémité
(ZL = ∞ ou plus généralement ZL > ZC).
À l’extrémité « charge » la tension réfléchie est en phase (0°) avec la tension incidente, la tension résultante (stationnaire) est la somme des deux amplitudes.
À cette même extrémité « charge » le courant réfléchi est en opposition de phase (180°) avec le courant incident, le courant résultant (stationnaire) est la différence des deux amplitudes.
La relation de phase de 0° et 180° entre signal réfléchi et incident ne s’applique que dans le cas où la charge est purement résistive.
L’impédance en chaque point de la ligne n’est que le rapport en amplitude et en phase de la tension résultante au courant résultant (stationnaire) en ce point Z = V / I .
Nous pouvons donc déduire en chaque point de la ligne, le type d'impédance, résistance et/ou réactance rencontré avec son signe et le circuit électrique équivalent.
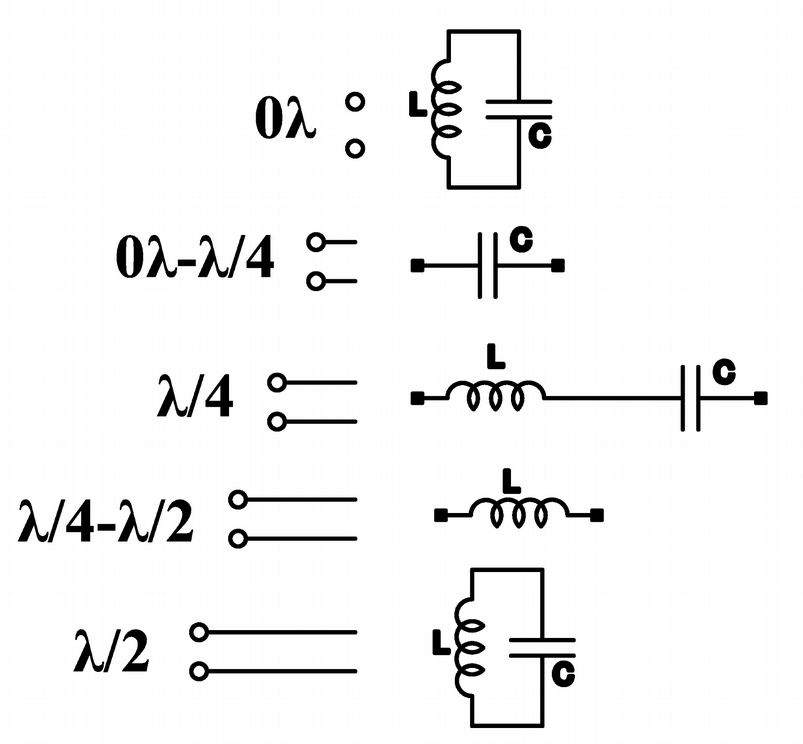
- à l'extrémité 0λ : le courant est minimum et la tension est maximum, suivant la loi d'ohm Z = V /0 = ∞ impédance est maximum, ce qui correspond au comportement d'un circuit résonnant parallèle.
- entre 0 λ à λ/4 : le courant diminue et la tension augmente, ce qui correspond à la charge d'un condensateur, le courant est en avance sur la tension, on est en présence d'une réactance capacitive.
- à λ/4 : le courant est maximum et la tension est minimum, l'impédance est minimum Z = 0/I = 0 ce qui correspond au comportement d'un circuit résonnant série.
- entre λ/4 et λ/2 : la tension diminue et le courant augmente, ce qui correspond à la charge d'une bobine d'induction, la tension est en avance sur le courant, on est en présence d'une réactance inductive.
- à λ/2 : le courant est minimum et la tension est maximum, l'impédance est maximum, on retrouve le circuit résonnant parallèle comme à l'extrémité.