La notion de mesure de grandeurs physiques est omniprésente dans le monde de la technique et aussi dans les activités des radioamateurs. Mais que mesure-t-on ou qu’est-ce que l’on croit mesurer ?
Avant de raccorder un appareil de mesure sur une électronique, il vaut mieux s’attendre à l’avance de ce que l’on doit obtenir comme mesure. Dans le cas contraire, il est plus que probable que la mesure n’ait aucune signification ou bien que l’électronique présente une anomalie, ce qui demandera alors une action corrective sur le montage électronique.
Une mesure, oui, mais dans quelles conditions ? Le protocole de mesure est aussi important que la mesure elle-même. En effet, pour qu’une mesure ait une signification, il y a lieu de décrire les conditions dans lesquelles cette mesure a été effectuée.
Voici deux exemples assez caractéristiques :
- 1. La mesure de sensibilité d’un récepteur FM s’exprime en μV ou en dBm, mais le résultat et les conditions de mesure sont les suivantes : 0,14 μV sur 50 Ω (c’est-à-dire -124 dBm) pour un signal modulant sinusoïdal de 1 kHz d’une amplitude donnée pour obtenir une excursion de fréquence de 3 kHz (NBFM) et pour un rapport signal sur bruit et distorsion de 12 dB SINAD (Signal Noise And Distortion) dans une bande passante du signal démodulé déterminée par un filtre psophométrique
caractérisé par la norme CCITT CCIR UIT P53 (Comité Consultatif International Télégraphique et Téléphonique, Comité Consultatif International pour la Radio, Union Internationale des Télécommunications) ; P53 : filtre passe bande d’un gabarit normé (de l’ordre de 300 Hz à 3500 Hz à -10 dB) avec une courbe de réponse bien spécifique (légèrement asymétrique). - La mesure du taux distorsion harmonique THD (Total Harmonic Distortion) s’exprime en pourcent ou en dB ; lorsque cette mesure tient compte du bruit superposé au signal on évoque l’appellation THD + N (Total Harmonic Distortion + Noise). Mais cette mesure n’a de signification que si l’on mentionne les conditions de mesure suivantes :
a. Spécifier le nombre d’harmoniques prises en compte (nombre de rangs);
b. Spécifier la bande passante de bruit;
c. Spécifier le type de filtre utilisé et ses caractéristiques (mesure pondérée);
d. Spécifier la fréquence du fondamental du signal de mesure ; ou bien;
e. Spécifier la bande de fréquence dans laquelle les fondamentales se situent, (mesure à plusieurs tons);
f. Spécifier l’amplitude du signal injecté à l’entrée du dispositif sous test ou l’amplitude du fondamental du signal mesuré;
g. Spécifier l’impédance de charge placée sur la sortie du dispositif sous test.
Les deux exemples ci-dessus illustrent bien que le protocole de mesure est aussi important que la mesure en elle-même. Autrement dit, en absence des conditions de mesure, une valeur de grandeur mesurée n’a aucune signification. Ceci indique aussi que la mesure n’est pas reproductible si elle n’est pas effectuée dans les mêmes conditions qui ont dues être décrites au préalable.
Dans cet article, on se propose d’examiner des mesures d’amplitude d’un signal alternatif, et d’une manière plus précise les mesures de tension efficace d’un signal (RMS, Root Mean Square, moyenne quadratique). Dans les exemples illustrés ci-dessous, le signal pourra être d’une forme sinusoïdale pure ou d’une autre forme : signal carré, impulsionnel, triangulaire, en forme de rampe, ou ce signal pourra être composé de deux sinusoïdes de même fréquence sous différents déphasages, ou encore être composé d’une sinusoïde (fondamentale) affectée d’un harmonique sous différents déphasages relatifs ou de différentes amplitudes.
Le but principal de ces mesures est d’illustrer l’importance du choix du type de voltmètre à utiliser en fonction du type de signal à mesurer et de comprendre la différence entre un voltmètre RMS (mesure d’une tension moyenne redressée et convertie en valeur efficace) et un voltmètre True RMS (mesure d’une tension efficace vraie).
Pour illustrer la forme des signaux mesurés, ceux-ci seront visualisés sur un oscilloscope numérique Tektronix TDS 7104 qui dispose de nombreuses possibilités de fonctions mathématiques et d’affichage numérique des mesures. Les tensions mesurées seront effectuées sur deux voltmètres RMS analogiques de types différents : un voltmètre RMS HP 400E « Average Responding » et un voltmètre RMS HP3400A (ou HP 3400B) « RMS responding ». Les mesures de tension efficace vraie seront contrôlées au moyen d’un multimètre numérique de chantier Fluke 28 True RMS et vérifiées au moyen d’un multimètre numérique étalon de laboratoire HP 3458A. Les signaux à mesurer seront obtenus à partir d’un générateur à double canaux HP 3326A et d’un générateur Agilent 33250A. Les générateurs seront toujours chargés sur une impédance de 50 Ω soit par l’entrée 50 Ω de l’oscilloscope lui-même, soit par une charge « traversante » (feedthru) de 50 Ω HP 10100C pour le raccordement sur un voltmètre à haute impédance.
Fig. 1 : Visualisation, sur un oscilloscope numérique, des signaux obtenus à partir de deux générateurs
Fig. 2 : Voltmètres analogiques (average responding et RMS responding), multimètre numérique True RMS de chantier et multimètre numérique étalon de laboratoire.
Historiquement les premiers instruments de mesure de tension sont les galvanomètres. Bien que ceux-ci soient avant tout des appareils de mesure de courant, on peut obtenir une mesure de tension avec des galvanomètres de résistance interne relativement élevée et mis en série avec une résistance formant le calibre de l’appareil (application de la loi d’Ohm). Les galvanomètres magnétoélectriques, c’est-à-dire à cadre mobile, appelés à mouvement d’Arsonval sont précis, sensibles et de résistance interne relativement élevée. En revanche, ce type de galvanomètre ne peut mesurer que du courant continu. Pour mémoire, il existe des galvanomètres ferromagnétiques et des galvanomètres thermiques capables de mesurer des courants alternatifs, mais ceux-ci manquent de précision ou de sensibilité. Ces deux derniers types sont plus adaptés à la mesure de courant qu’à la mesure de tension.
Ainsi, un voltmètre analogique pour la mesure de tensions en courant alternatif est constitué d’un galvanomètre à cadre mobile précédé d’un redresseur en pont à diodes. Un net progrès technologique de ces voltmètres est celui des voltmètres à tubes : VTVM, Vacuum Tube Volt Meter. Les VTVM ont l’avantage d’avoir une résistance d’entrée très élevée (de l’ordre de 10 MΩ à 100 MΩ) et qui n’est pas dépendante du calibre. Il est donc possible de mesurer un potentiel (une tension) sans consommer d’énergie sur la source du potentiel à mesurer. L’exemple classique est celui de la mesure du potentiel de grille de commande d’une triode ou d’une penthode sans perturber la polarisation de cette grille. La version moderne du VTVM est le voltmètre à amplificateur d’entrée constitué de transistors à effet de champ (FET Field Effect Transistor). Quoi qu’il en soit, dans chaque version de voltmètre, le principe reste le même : redresser le courant alternatif pour le transformer en courant continu et mesurer ce dernier au moyen d’un galvanomètre.
Qu’est-ce qu’une mesure de tension en courant alternatif ?
Voici une question banale, mais la réponse, quoiqu’elle puisse parfois sembler subtile, est parfaitement définie et bien connue de tous. Pour rester abordable sans trop s’appesantir, nous en faisons ci-dessous un bref rappel avec un peu de mathématique, juste ce qu’il faut.
Un signal alternatif est une grandeur variable dans le temps d’une façon périodique et dont on peut définir sa période (et donc sa fréquence), son amplitude et ses alternances. L’amplitude correspond à la valeur de crête du signal (tension peak). La mesure de différence de potentiel entre la valeur maximale instantanée et la valeur minimale instantanée correspond à la valeur de tension crête à crête (tension peak to peak). La valeur moyenne d’un signal périodique, sur une période de celui-ci, correspond à la composante continue qui est superposée à la partie variable du signal. Un courant purement alternatif est caractérisé par une valeur moyenne nulle.
Et la valeur efficace dans tout cela ?
La valeur efficace est celle qui caractérise le mieux au sens physique la nature d’une tension alternative car elle représente son effet en termes d’énergie (c’est-à-dire son efficacité) lorsque cette tension est appliquée à une charge. On définit donc la valeur efficace comme suit.
Tension efficace (RMS) : valeur de tension continue qui apporterait une même dissipation de puissance (ou d’énergie par unité de temps) que celle qui est apportée par la tension alternative du signal à mesurer si elle était appliquée à une même résistance.
La valeur efficace d’un signal est :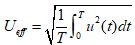 
où : T représente la période et u (t) représente la variation du signal en fonction du temps.
Il s’agit d’une moyenne quadratique : racine carrée de la moyenne des carrés (RMS). La moyenne des carrés est représentée par l’intégrale sur une période.
Et la valeur moyenne, où intervient-elle ?
Comme un voltmètre alternatif et constitué d’un redresseur et d’un galvanomètre, c’est la valeur moyenne de la tension redressée (aussi appelée valeur absolue moyenne) qui est mesurée par le galvanomètre et non pas la valeur efficace.
La valeur moyenne redressée d’un signal est :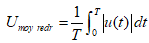 
où : T représente la période et u (t) représente la variation du signal en fonction du temps.
Il s’agit d’une moyenne arithmétique, représentée par l’intégrale sur une période.
Mais alors, comment mesurer une tension efficace à partir d’une tension moyenne redressée ?
C’est ici qu’intervient la notion de facteur de forme du signal. Le facteur de forme (Ff) est par définition le rapport de la valeur efficace sur la valeur moyenne redressée :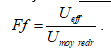 
En effet, pour graduer le galvanomètre en valeur de tension efficace à partir d’une tension moyenne redressée, il suffit d’intercaler un dispositif correcteur entre le redresseur et le galvanomètre. En d’autres mots, il suffit de multiplier la valeur de la tension moyenne par un facteur correcteur, ici le facteur de forme, afin d’obtenir une mesure de tension efficace. Mais, comme son nom l’indique, le facteur de forme dépend de la forme du signal. Le facteur de forme d’un signal sinusoïdal n’est pas le même que celui d’un signal carré ou triangulaire ou encore d’un signal sinusoïdal affecté de distorsion due à la présence d’harmoniques et de bruit.
Dans la majeure partie des applications électriques ou électroniques, le signal alternatif dont il faut mesurer la tension efficace est de forme sinusoïdale. Le facteur de forme correcteur de la graduation du galvanomètre sera donc par convention celui d’un signal sinusoïdal.
Pour un signal sinusoïdal, le facteur de forme est :
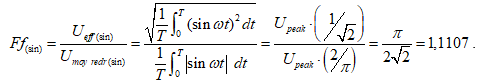
Il reste une dernière étape à compléter pour constituer un voltmètre alternatif. La tension à la sortie du redresseur est une tension continue pulsée en forme d’arcade de sinusoïdes. Pour obtenir la valeur moyenne de cette tension pulsée, on place un filtre passe-bas à la sortie du redresseur à diodes. Voici donc le schéma bloc d’un voltmètre alternatif RMS basé sur la tension moyenne d’un courant redressé. On appellera ce type de voltmètre : RMS average responding.
Fig. 3 : Schéma bloc d’un voltmètre alternatif RMS average responding. Ce principe est appliqué auvoltmètre analogique HP 400E.
Le facteur correcteur de tous les voltmètres RMS Average Responding correspond toujours au facteur de forme d’un signal sinusoïdal pur : 1,11.
On constatera que les mesures sur le voltmètre RMS Average Responding sont justes mais uniquement pour un signal de forme sinusoïdale pure ; les mesures sont par excès pour un signal carré et sont par défaut pour un signal triangulaire. L’explication se trouve ci-dessous après calculs des intégrales définies des différentes fonctions.
Pour un signal carré symétrique (rapport cyclique de 50 %), le facteur de forme est :
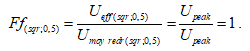
Pour un signal triangulaire symétrique, le facteur de forme est :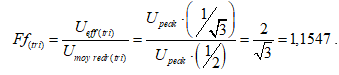
La valeur « mesurée » – c’est-à-dire lue sur l’appareil – d’un signal d’une forme donnée et d’une valeur efficace donnée au moyen d’un voltmètre RMS Average Responding est :
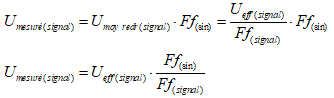
Par exemple, pour un signal d’une valeur efficace de 900 mVRMS fourni par un générateur, les valeurs lues par le voltmètre RMS Average Responding pour les signaux des formes suivantes seront
pour un signal carré symétrique :
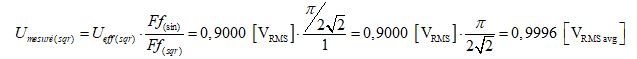
qui est une valeur lue par excès (voir figures 14, 15, 16 et 17) ;
pour signal triangulaire symétrique :
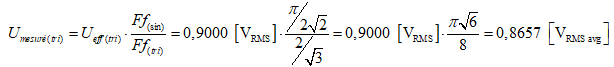
qui est une valeur lue par défaut (voir figures 19, 20, 21 et 22).
Pour retrouver la valeur efficace juste (sans erreur de lecture), il faudra corriger les valeurs lues par le voltmètre RMS Average Responding selon les relations suivantes :
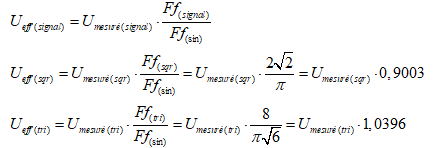
Comment mesurer une tension efficace vraie sur un signal de forme quelconque ?
La solution est d’utiliser un voltmètre True RMS ou voltmètre RMS responding.
Quelle solution technologique faut-il adopter pour les mesures de tension True RMS ?
Une solution est d’utiliser une résistance accouplée à un thermocouple et de se ramener à la définition de la mesure de tension efficace : valeur de tension continue qui apporterait une même dissipation de puissance que celle qui est apportée par la tension alternative du signal à mesurer si elle était appliquée à une même résistance.
Pourquoi un thermocouple ?
Lorsqu’on applique une tension alternative (ou continue) aux bornes d’une résistance, celle-ci dissipe de l’énergie par effet Joules sous la forme d’une quantité de chaleur. Cette quantité de chaleur par unité de temps fait élever la température de la résistance jusqu’à un équilibre thermique qui est fonction de l’environnement dans lequel se situe la résistance. Le thermocouple mesure l’élévation de température de la résistance. On peut en déduire la valeur de tension efficace vraie appliquée à la résistance.
En pratique, on utilise deux résistances et deux thermocouples. Chaque résistance est accouplée respectivement à un thermocouple. Chaque résistance associée à son thermocouple se situe dans une ampoule de verre. Il y a donc deux ampoules de verre et celles-ci sont placées ensemble dans un bloc isotherme. La tension alternative est appliquée à la première résistance par l’intermédiaire d’un amplificateur à courant alternatif. Les deux thermocouples sont reliés en série et en opposition de polarités. La tension continue différentielle des thermocouples est appliquée à un amplificateur à courant continu. La sortie de cet amplificateur est raccordée à la deuxième résistance et à un galvanomètre relié en dérivation sur celle-ci. Le système étant donc bouclé, la tension continue lue au galvanomètre et qui est donc appliquée à la deuxième résistance doit dissiper la même quantité d’énergie dans cette deuxième résistance que celle qui est dissipée dans la première résistance par la tension alternative. Le système est à l’équilibre lorsque la tension différentielle s’annule entre les deux thermocouples raccordés en opposition, ce qui signifie que les deux thermocouples sont à la même température et donc les deux résistances le sont aussi. Ceci nous ramène bien à la définition de la tension efficace. Voir schéma à la figure suivante.
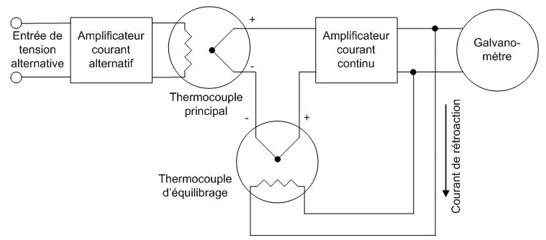
Fig. 4 : Schéma bloc d’un voltmètre alternatif RMS Responding ou True RMS à thermocouples. Ce principe est appliqué aux voltmètres analogiques RMS Responding HP 3400A et HP 3400B.
Voici ce que donnent les relevés de mesure d’un signal sinusoïdal, carré et triangulaire sur un oscilloscope, sur des voltmètres analogiques et sur des voltmètres numériques. Pour ce premier lot d’expériences, nous prendrons chaque fois un signal d’une fréquence de 1 kHz et d’une tension efficace vraie de 900 mVRMS à la sortie du générateur Agilent 33250A.
Pour visualiser les mesures sur l’oscilloscope, une mesure True RMS sera activée sur un canal, une trace issue d’une fonction mathématique sera définie pour correspondre au schéma bloc d’un voltmètre RMS average responding, c’est-à-dire : Vrms avg = 1,11.|u(t) (la fonction de la valeur absolue simule le redressement), et enfin une mesure de la valeur moyenne du résultat de cette fonction mathématique sera activée pour obtenir le résultat de la fonction complète :VRms avg =1,11.{u(t)|}
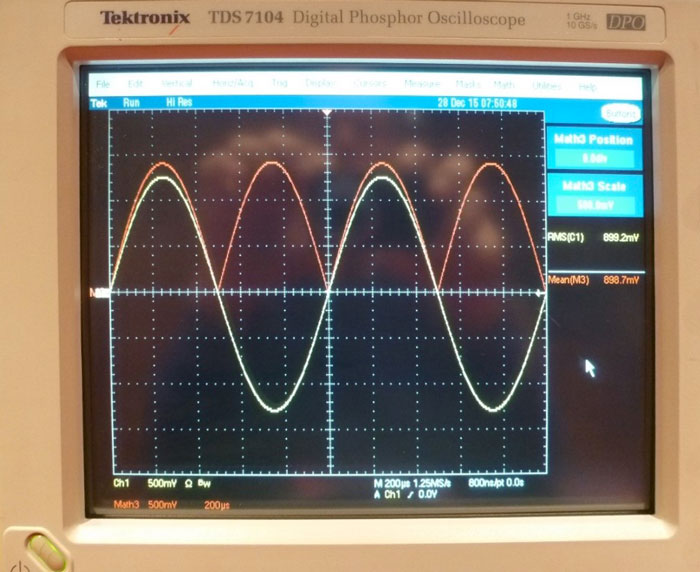
Fig. 5 : Oscilloscope numérique disposant de fonctions mathématiques et d’affichage de mesures.
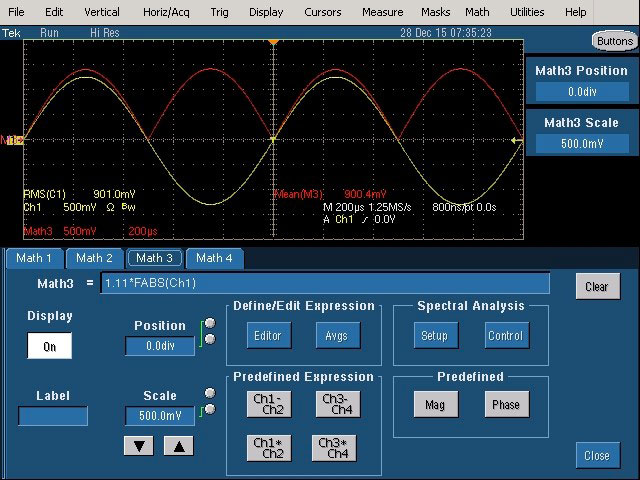
Fig. 6 : Activation de la fonction mathématique (Math 3) simulant le fonctionnement d’un voltmètre RMS average responding.
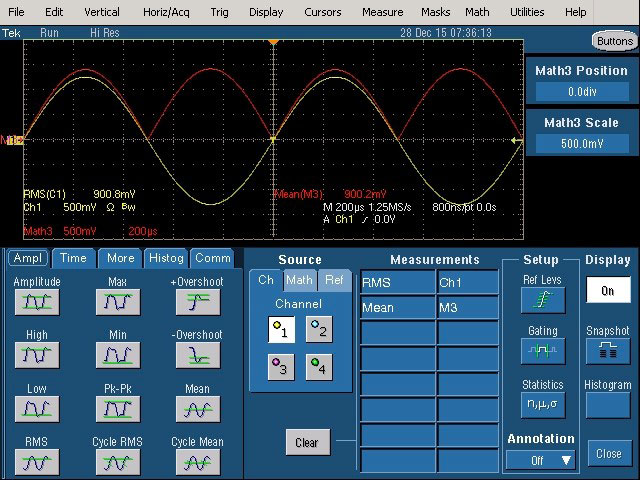
Fig. 7 : Activation d’une mesure RMS (Canal 1) et d’une mesure de moyenne (Math 3).
Fig. 8 : Consigne d’un signal sinusoïdal 1 kHz 900 mVRMS au générateur.
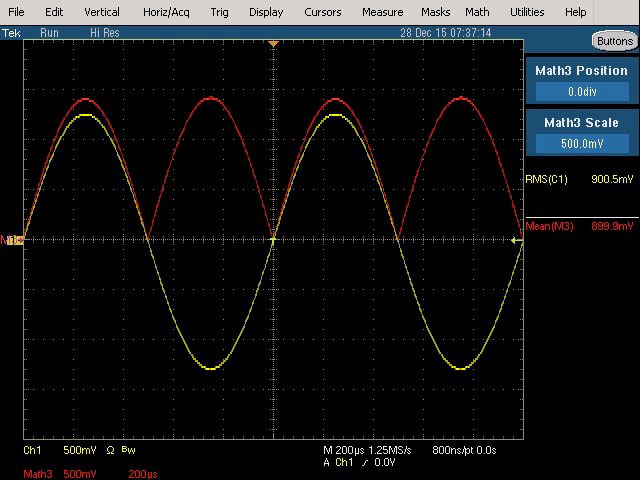
Fig. 9 : Relevé sur l’oscilloscope d’une tension True RMS de 900,5 mV et en simulation RMS average responding de 899,9 mVRMS. Les deux mesures sont cohérentes pour un signal sinusoïdal pur.
Fig. 10 : (à gauche) Grandeur mesurée (sinusoïdal) HP 400E average responding de 905 mVRMS. Fig. 11 : (à droite) Grandeur mesurée (sinusoïdal) HP 3400A RMS responding de 902 mVRMS.
Fig. 12 : Grandeur mesurée (sinusoïdal) HP 3458A True RMS de 904,1 mVRMS.
Les deux mesures analogiques et la mesure numérique sont cohérentes pour un signal sinusoïdal pur. La simulation de mesure average responding sur l’oscilloscope est en accord avec celle du voltmètre analogique average responding pour un signal sinusoïdal.
Fig. 13 : Consigne d’un signal carré de rapport cyclique de 50 % 1 kHz 900 mVRMS au générateur.
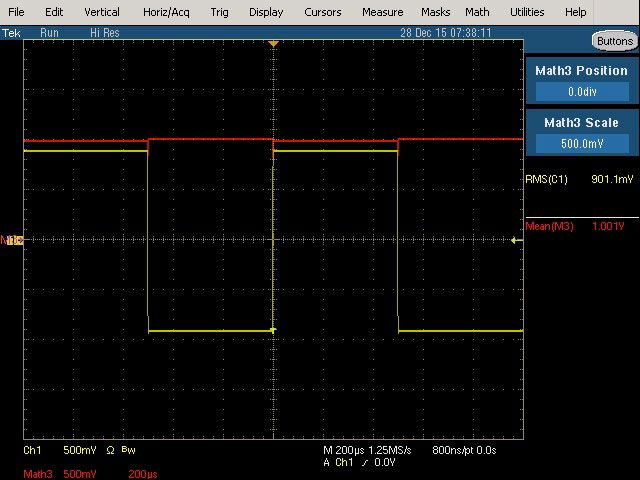
Fig. 14 : Relevé sur l’oscilloscope d’une tension True RMS de 901,1 mV et en simulation RMS average responding de 1,001 VRMS. Les deux mesures ne sont plus cohérentes pour un signal carré.
fig.15 : (à gauche) Grandeur mesurée (carré) HP 400E average responding de 1,000 VRMS. Fig. 16 : (à droite) Grandeur mesurée (carré) HP 3400A RMS responding de 900 mVRMS.
Fig. 17 : Grandeur mesurée (carré) HP 3458A True RMS de 899,6 mVRMS.
La mesure analogique average responding n’est plus cohérente (valeur par excès d’un facteur de 1,1107) avec la mesure analogique RMS responding ni avec la mesure numérique True RMS pour un signal carré. En revanche, la mesure analogique RMS responding reste cohérente avec la mesure numérique True RMS pour un signal carré.
La simulation de mesure average responding sur l’oscilloscope reste en accord avec celle du voltmètre analogique average responding pour un signal carré.
Fig. 18 : Consigne d’un signal triangulaire symétrique (50 %) 1 kHz 900 mVRMS au générateur.
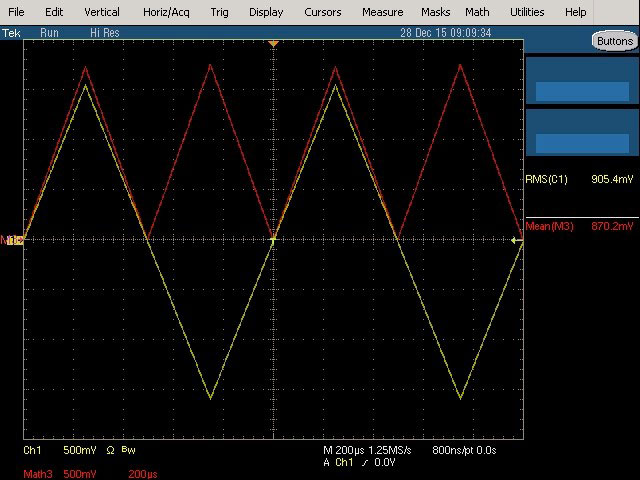
Fig. 19 : Relevé sur l’oscilloscope d’une tension True RMS de 905,4 mV et en simulation RMS average responding de 870,2 mVRMS. Les deux mesures ne sont plus cohérentes pour un signal triangulaire.
Fig. 20 : (à gauche) Grandeur mesurée (triangle) HP 400E average responding de 866 mVRMS. Fig. 21 : (à droite) Grandeur mesurée (triangle) HP 3400A RMS responding de 900 mVRMS.
Fig. 22 : Grandeur mesurée (triangle) HP 3458A True RMS de 902,7 mVRMS.
La mesure analogique average responding n’est plus cohérente (valeur par défaut d’un facteur de 0,9619) avec la mesure analogique RMS responding ni avec la mesure numérique True RMS pour un signal triangulaire. En revanche, la mesure analogique RMS responding reste cohérente avec la mesure numérique True RMS pour un signal triangulaire.
La simulation de mesure average responding sur l’oscilloscope reste en accord avec celle du voltmètre analogique average responding pour un signal triangulaire.
Peut-on mesurer facilement un signal rectangulaire positif d’un rapport cyclique très faible, c’est-à-dire lorsque ce signal tend à devenir un signal impulsionnel ?
La réponse est oui, mais jusqu’à une certaine limite. Cette limite est celle de la bande passante de l’appareil de mesure. En effet, plus le rapport cyclique diminue et plus le spectre des fréquences s’élargit. L’enveloppe du spectre est de la forme .
C’est ici qu’intervient la notion de facteur de crête d’un signal (Crest Factor).
Le facteur de crête (Fc) est par définition le rapport de la valeur de crête sur la valeur efficace :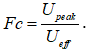
Pour un signal rectangulaire positif et d’un rapport cyclique α, on a :
Fig. 23 : Voltmètre RMS HP 3400A : RMS Responding.
Caractéristique de facteur de crête de 10 : 1 (à fond d’échelle).
Jusqu’à présent, nous avons relevé des mesures de tension RMS sur des signaux de formes bien déterminées et relativement simples : sinusoïdal pur, carré, triangulaire. Qu’en est-il pour des signaux composés ou signaux complexes ?
C’est ici qu’un voltmètre RMS responding ou True RMS offre tout son bénéfice. En effet, on ne peut pas toujours caractériser à l’avance sous forme mathématique un signal sinusoïdal affecté de distorsion harmonique et de bruit. Ce type d’appareil de mesure True RMS est indispensable pour pouvoir caractériser correctement la mesure du signal démodulé à la sortie d’un récepteur radiofréquence car ce signal est affecté de distorsion et de bruit dans les mesures spécifiques de sensibilité du récepteur, des produits d’intermodulation du troisième ordre (IMD) et du point d’interception du troisième ordre (IP3).
Pour ce deuxième lot d’expériences, nous prendrons chaque fois un signal sinusoïdal d’une fréquence fondamentale de 1 kHz et d’une tension efficace vraie de 100 mVRMS à la sortie du premier canal du générateur HP 3326A. À la sortie du deuxième canal du générateur, nous prendrons un harmonique du deuxième ou troisième rang dont nous allons faire varier la phase relative avec le fondamental.
La visualisation des signaux et mesures sur l’oscilloscope sera effectuée comme suit. Une mesure True RMS sera activée sur le canal 1 et une mesure True RMS sera activée sur le canal 2.
Une trace issue d’une fonction mathématique sera définie pour effectuer la composition des deux signaux (fondamental plus harmonique) par addition des deux canaux :
Math 1=(canal1+canal2)
Une mesure True RMS sera activée sur le résultat de la fonction Math 1, c’est-à-dire sur le signal composé par addition des deux canaux. Cette mesure représente celle de la tension efficace vraie d’un signal affecté de distorsion harmonique :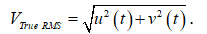 
Ceci permettra de vérifier que la mesure d’une tension efficace vraie est le résultat d’une moyenne quadratique : RMS, Root Mean Square et que la phase relative entre le fondamental et l’harmonique n’affecte pas la mesure.
Une autre trace sera activée pour simuler le fonctionnement d’un voltmètre RMS average responding, c’est-à-dire :
Math 2 = 1,11.(canal 1 + canal 2)|
Une mesure de la valeur moyenne (tension moyenne redressée) sera activée sur le résultat de la fonction Math 2, c’est-à-dire : VRMS avg = 1,11.{|(u(t) + v(t)|} Ceci permettra d’illustrer la mesure erronée d’un voltmètre RMS average responding et nous pourrons même constater que l’erreur de mesure est en outre dépendante de la phase relative entre le fondamental et l’harmonique.
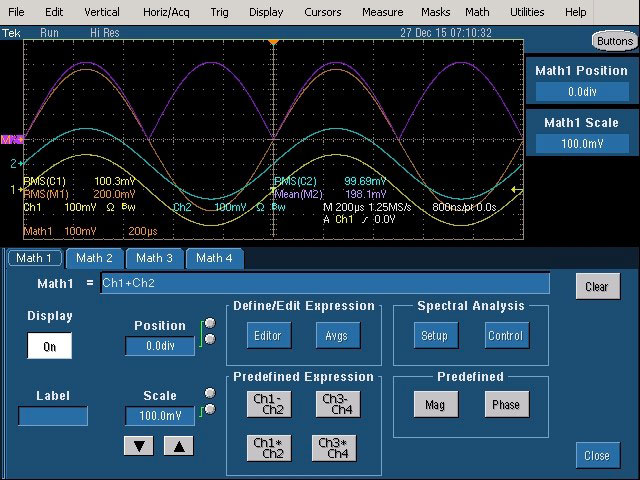
Fig. 24 : Activation de la fonction mathématique (Math 1) réalisant la composition du signal fondamental et d’un harmonique par addition des signaux.
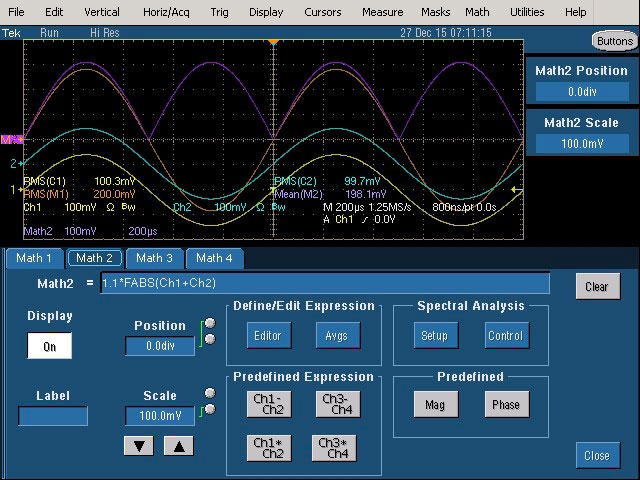
Fig. 25 : Activation de la fonction mathématique (Math 2) simulant le fonctionnement d’un voltmètre RMS average responding.
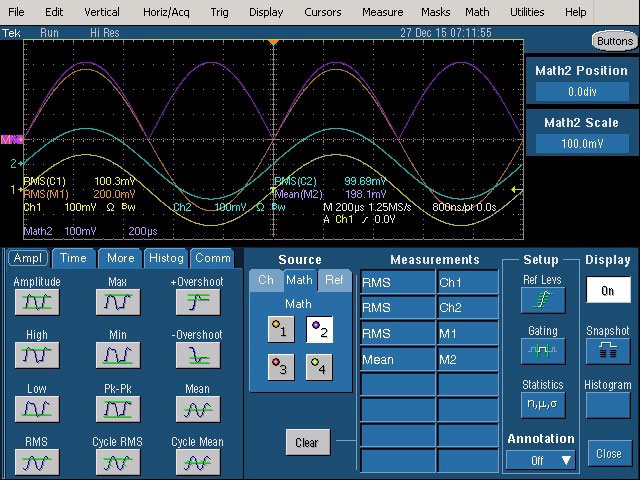
Fig. 26 : Activation d’une mesure RMS (Canal 1), d’une mesure RMS (Canal 2), d’une mesure RMS des signaux composés (Math 1 = Canal 1 + Canal 2) qui représente la mesure d’un voltmètre True RMS et enfin d’une mesure de moyenne (Math 2) qui représente la mesure d’un voltmètre RMS average responding.
Fig. 27 : Pour se familiariser avec les oscillogrammes qui vont suivre, voici une composition de deux sinusoïdes de même fréquence (1 kHz), de même amplitude (100 mVRMS) et qui sont en phase (ondes constructives). La légende de couleur des traces est : jaune = canal 1 ; cyan = canal 2 ; brun orangé (Math 1) = somme des canaux 1 et 2 ; magenta (Math 2) = simulation du fonctionnement d’un voltmètre RMS average responding. L’affichage des mesures à la droite de l’écran est de la même légende de couleur et l’objet de ces mesures a été décrit à la figure précédente.
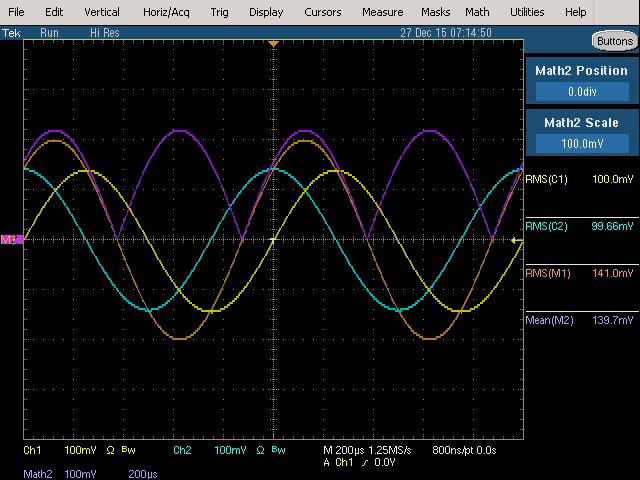
Fig. 28 : Idem que figure précédente mais avec un déphasage de 90°.
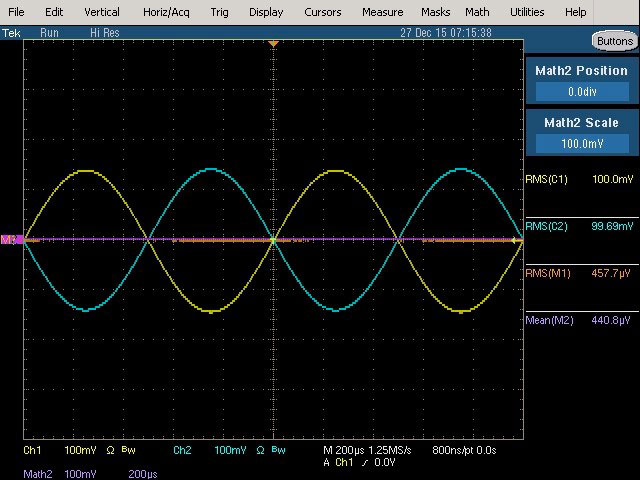
Fig. 29 : Idem que figure précédente mais avec un déphasage de 180° (ondes destructives).
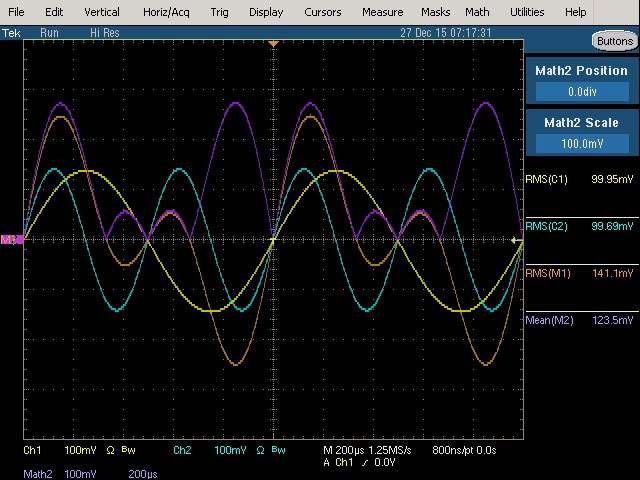
Fig. 30 : Fondamental (1 kHz, 100 mVRMS) et 2ème harmonique (2 kHz, 100 mVRMS) avec phase relative de 0°. L’origine des phases est visualisée au centre de l’écran.
Mesure True RMS : 141,1 mVRMS qui vérifie la relation de la moyenne quadratique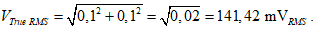 
Cette mesure est confirmée par celle du voltmètre analogique RMS responding HP 3400A, par le multimètre de chantier True RMS Fluke 28 et par le multimètre étalon de laboratoire HP 3458A.
Mesure RMS average responding : 123,5 mVRMS qui est une mesure erronée. Le voltmètre analogique RMS average responding HP 400E effectue la même mesure (124 mVRMS). Ceci démontre immédiatement la limitation des capacités de mesure d’un voltmètre average responding.
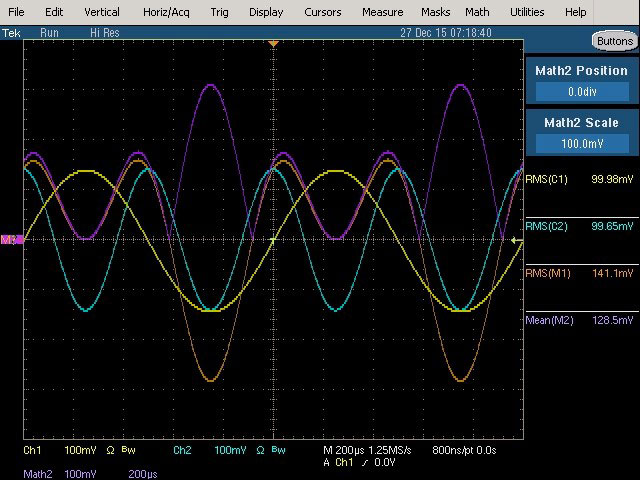
Fig. 31 : Fondamental (1 kHz, 100 mVRMS) et 2ème harmonique (2 kHz, 100 mVRMS) avec phase relative de 90°. L’origine des phases est visualisée au centre de l’écran.
Mesure True RMS : 141,1 mVRMS qui reste inchangée à 90° de phase par rapport à la mesure effectuée à 0 ° de phase. Même mesure sur les voltmètres RMS responding et True RMS.
Mesure RMS average responding : 128,5 mVRMS qui non seulement est erronée mais qui est différente à 90° de phase par rapport à la mesure effectuée à 0° de phase. Mesure similaire avec le voltmètre analogique RMS average responding.
On remarquera que la forme d’onde du signal composé est différente par rapport à celle de la figure précédente.
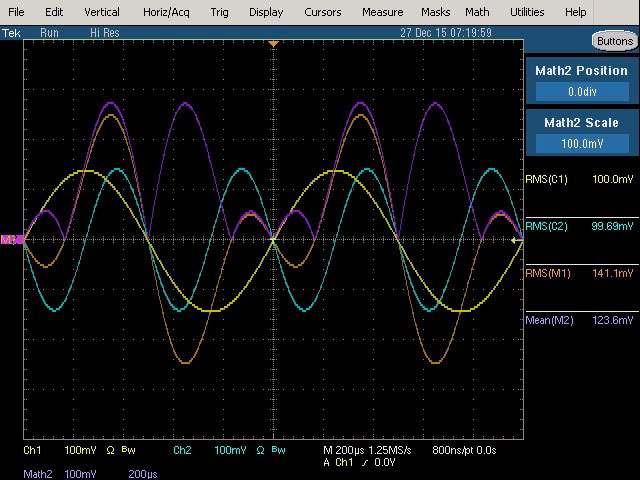
Fig. 32 : Fondamental (1 kHz, 100 mVRMS) et 2ème harmonique (2 kHz, 100 mVRMS) avec phase relative de 180°. L’origine des phases est visualisée au centre de l’écran.
Mesure True RMS : 141,1 mVRMS qui reste inchangée à 180° de phase par rapport à la mesure effectuée à 0 ° et à 90° de phase. Même mesure sur les voltmètres RMS responding et True RMS.
Mesure RMS average responding : 123,6 mVRMS qui non seulement est erronée mais qui est différente à 180° de phase par rapport à la mesure effectuée à 90° de phase, mais comparable à 180° de phase par rapport à la mesure effectuée à 0° de phase. Mesure similaire avec le voltmètre analogique RMS average responding.
On remarquera que la forme d’onde du signal composé à 180° de phase est différente par rapport à celle de la figure précédente à 90° de phase mais qu’elle ressemble à la figure de l’oscillogramme à 0° de phase. La seule différence est un déphasage d’ensemble du signal composé à 180° de phase entre le fondamental et l’harmonique par rapport l’oscillogramme à 0° de phase entre ceux-ci.
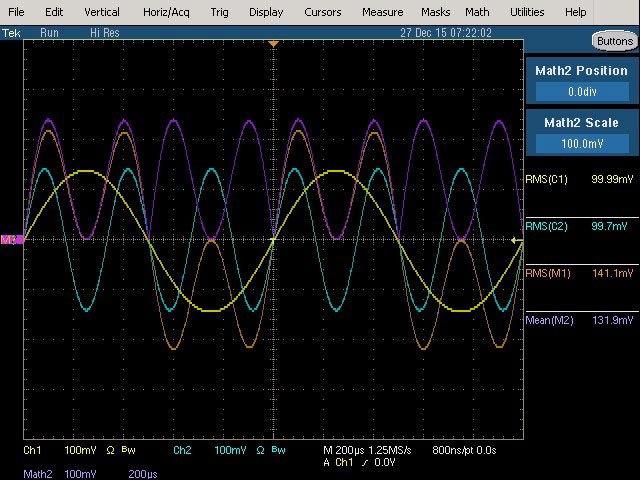
Fig. 33 : Fondamental (1 kHz, 100 mVRMS) et 3ème harmonique (3 kHz, 100 mVRMS) avec phase relative de 0°. L’origine des phases est visualisée au centre de l’écran.
Mesure True RMS : 141,1 mVRMS qui reste inchangée avec le troisième harmonique par rapport aux mesures effectuées avec le second harmonique. Même mesure sur les voltmètres RMS responding et True RMS.
Mesure RMS average responding : 131,9 mVRMS qui non seulement est erronée mais qui est encore différente des mesures précédentes. Mesure similaire avec le voltmètre analogique RMS average responding.
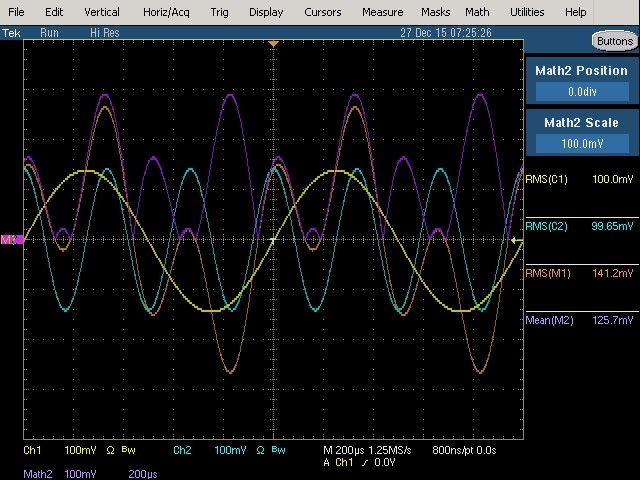
Fig. 34 : Fondamental (1 kHz, 100 mVRMS) et 3ème harmonique (3 kHz, 100 mVRMS) avec phase relative de 90°. L’origine des phases est visualisée au centre de l’écran.
Mesure True RMS : 141,2 mVRMS qui reste inchangée par rapport aux mesures précédentes. Même mesure sur les voltmètres RMS responding et True RMS.
Mesure RMS average responding : 125,7 mVRMS qui non seulement est erronée mais qui est encore différente des mesures précédentes. Mesure similaire avec le voltmètre analogique RMS average responding.
On remarquera que la forme d’onde du signal composé est différente par rapport à celle de la figure précédente.
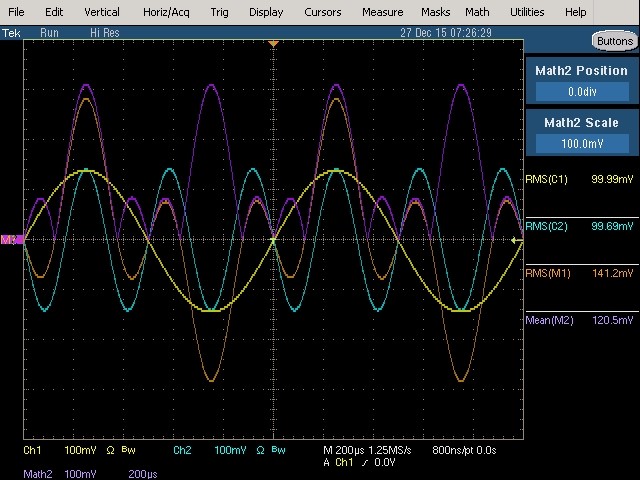
Fig. 35 : Fondamental (1 kHz, 100 mVRMS) et 3ème harmonique (3 kHz, 100 mVRMS) avec phase relative de 180°. L’origine des phases est visualisée au centre de l’écran.
Mesure True RMS : 141,2 mVRMS qui reste inchangée par rapport aux mesures précédentes. Même mesure sur les voltmètres RMS responding et True RMS.
Mesure RMS average responding : 120,5 mVRMS qui non seulement est erronée mais qui est encore différente des mesures précédentes. Mesure similaire avec le voltmètre analogique RMS average responding.
On remarquera que la forme d’onde du signal composé est différente par rapport à celle de la figure précédente.
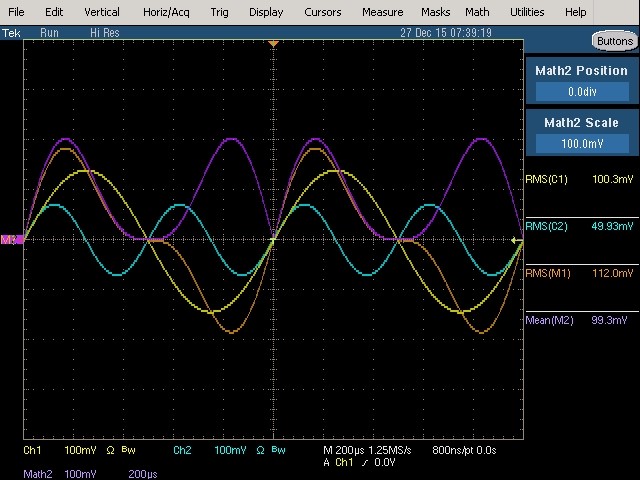
Fig. 36 : Fondamental (1 kHz, 100 mVRMS) et 2ème harmonique (2 kHz, 50 mVRMS) avec phase relative de 0°. L’origine des phases est visualisée au centre de l’écran.
Cet oscillogramme est similaire à celui qui a été réalisé à la figure 30, mais le niveau de l’harmonique a été réduit à 50 mVRMS.
Mesure True RMS : 112,0 mVRMS qui vérifie toujours la relation de moyenne quadratique 
Cette mesure est confirmée par celle du voltmètre analogique RMS responding HP 3400A, par le multimètre de chantier True RMS Fluke 28 et par le multimètre étalon de laboratoire HP 3458A.
Mesure RMS average responding : 99,3 mVRMS qui est toujours une mesure erronée. Le voltmètre analogique RMS average responding HP 400E effectue une mesure similaire.
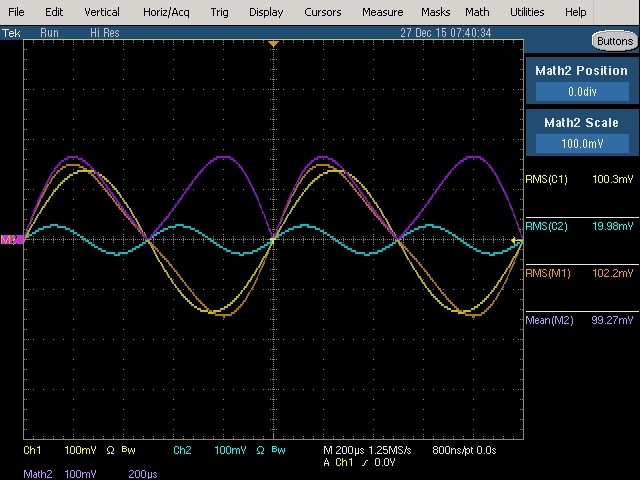
Fig. 37 : Fondamental (1 kHz, 100 mVRMS) et 2ème harmonique (2 kHz, 20 mVRMS) avec phase relative de 0°. L’origine des phases est visualisée au centre de l’écran.
Cet oscillogramme est similaire à celui qui a été réalisé à la figure précédente, mais le niveau de l’harmonique a encore été réduit jusqu’à 20 mVRMS.
Mesure True RMS : 102,2 mVRMS qui vérifie toujours la relation de moyenne quadratique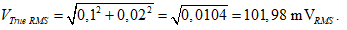 
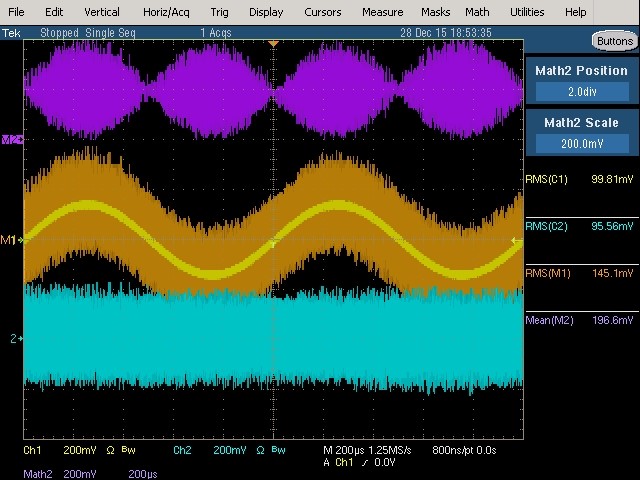
Fig. 38 : Signal sinusoïdal (1 kHz, 100 mVRMS) avec bruit blanc superposé (100 mVRMS), bande passante 20 MHz.
Voici une troisième expérience qui et probablement la mesure la plus difficile pour un voltmètre RMS conventionnel average responding. Seul un voltmètre RMS responding ou True RMS est capable de donner une mesure significative pour un signal superposé de bruit. Ce type de mesure est particulièrement critique lorsque l’on effectue des relevés de sensibilité de récepteurs radiofréquence ou bien dans le cas où l’on doit déterminer le plancher de bruit d’un appareil (Noise Floor). En effet, le niveau minimum que peut discerner un récepteur (plancher de bruit) s’effectue pour un rapport signal sur bruit de 3 dB pour une bande passante définie. Cela signifie que l’énergie du signal utile est à peine le double de celle du bruit. Ce niveau de bruit devient dès lors prépondérant dans la mesure de la tension efficace vraie du signal plus le bruit ou dans la mesure de la tension efficace vraie du bruit seul avant de pouvoir déterminer une augmentation de 3 dB du signal au-dessus du bruit.
Sur la figure ci-dessus, la mesure True RMS est correcte et attendue : 145,1 mVRMS en pratique (141,42 mVRMS en théorie selon la moyenne quadratique). Cette mesure est confirmée par les voltmètres RMS responding et True RMS. Ce n’est pas du tout le cas de la mesure RMS average responding qui est complètement erronée : 196,6 mVRMS. Le voltmètre analogique RMS average responding donne une mesure similaire mais qui est de toute façon erronée.
Cas particulier : mesure de signaux impulsionnels.
Il s’agit de signaux rectangulaires symétriques dont on peut faire varier le rapport cyclique. Ce type de signal n’est plus du type alternatif pur (sauf pour un rapport cyclique de 50 %) mais bien du type périodique. C’est-à-dire que le signal est composé d’une partie variable et d’une composante continue (tension moyenne). La composante continue est fonction du rapport cyclique du signal rectangulaire symétrique. La partie strictement variable est aussi fonction du rapport cyclique (voir plus loin). On trouvera l’application de tels signaux dans les dispositifs à Modulation de Largeur d’Impulsion (MLI, PWM : Pulse Width Modulation).
Afin de mesurer la tension efficace vraie d’un tel type de signal, il y a lieu de faire la distinction entre la partie strictement variable du signal et le signal total : partie variable et composante continue (AC+DC). Seuls les multimètres de laboratoire sont équipés pour mesurer distinctement la valeur efficace vraie du signal total (AC+DC), la partie strictement variable (AC) et la composante continue (DC).
La tension efficace vraie du signal rectangulaire symétrique total (AC+DC) est :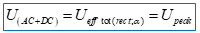
On remarque que cette valeur (AC+DC) est indépendante du rapport cyclique. La valeur moyenne (non redressée) d’un signal rectangulaire symétrique de rapport cyclique α est :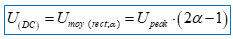
La tension efficace vraie du signal total (AC+DC) doit vérifier la relation de la moyenne quadratique :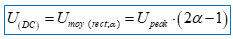ce qui donne pour un signal rectangulaire symétrique :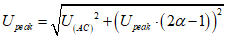 
Or les voltmètres True RMS et RMS responding ne mesurent que la partie strictement variable des signaux (AC) que l’on appelle aussi l’ondulation : U(AC).
De la relation de la moyenne quadratique qui précède, on peut en déduire que :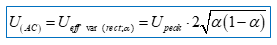
Faut-il rappeler qu’un voltmètre RMS average responding est parfaitement incapable d’effectuer une mesure correcte pour un tel type de signal.
Les mesures distinctes de U(AC+DC), U(AC), et U(DC) sont intéressantes pour le relevé de l’ondulation résiduelle d’une alimentation régulée lorsque l’on veut exprimer l’ondulation en termes de valeur de tension efficace vraie.
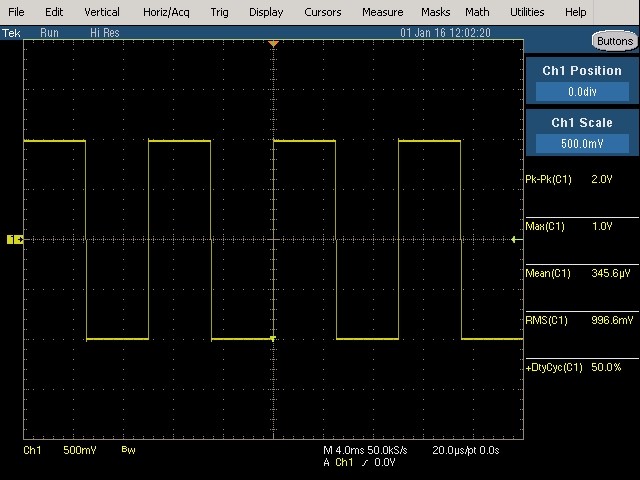
Fig. 39 : Signal rectangulaire symétrique (100 Hz, 2 Vpp) d’un rapport cyclique de 50 % (signal carré symétrique). Mesures de Upp, Upeak, Umoy, URMS (AC+DC), rapport cyclique.
Vérifions les mesures décrites ci-dessus pour un signal rectangulaire symétrique dont le rapport cyclique est de 50 % (c’est-à-dire un signal carré symétrique). Les relations mathématiques établies ci-dessus doivent au moins confirmer les mesures pour un signal carré symétrique comme cela avait été illustré aux figures 13, 14, 15, 16 et 17.
Sur l’oscilloscope, l’entrée verticale est paramétrée sur « DC » et non pas sur « AC ». Ainsi, l’oscillogramme et les mesures qui s’y rapportent concernent la totalité du signal rectangulaire, c’est-à-dire U(AC+DC).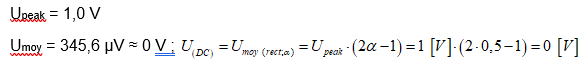 
La valeur moyenne est nulle car il s’agit ici d’un signal alternatif pur (signal carré). URMS (AC+DC) = 996,6 mVRMS ≈ 1 VRMS (= Upeak)
Fig. 40 : Mesures d’un signal rectangulaire symétrique (100 Hz, 2 Vpp) d’un rapport cyclique de 50 % (signal carré symétrique). Mesures de la tension efficace vraie URMS (AC) au moyen d’un voltmètre analogique RMS responding et d’un multimètre True RMS.
Ici, nous vérifions les mesures de la composante strictement variable d’un signal rectangulaire symétrique dont le rapport cyclique est de 50 %.
La relation mathématique de la mesure de U(AC) doit se vérifier.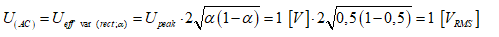
Sur le voltmètre analogique RMS responding, la mesure de U(AC) = 1,0 VRMS.
Sur le multimètre true RMS, la mesure de U(AC) = 1,000 VRMS.
Les mesures relevées ci-dessus sont des vraies mesures sur le signal rectangulaire. On remarquera la précision redoutable de ces appareils. Tout ceci vérifie ce que nous avions déjà constaté pour un signal carré symétrique.
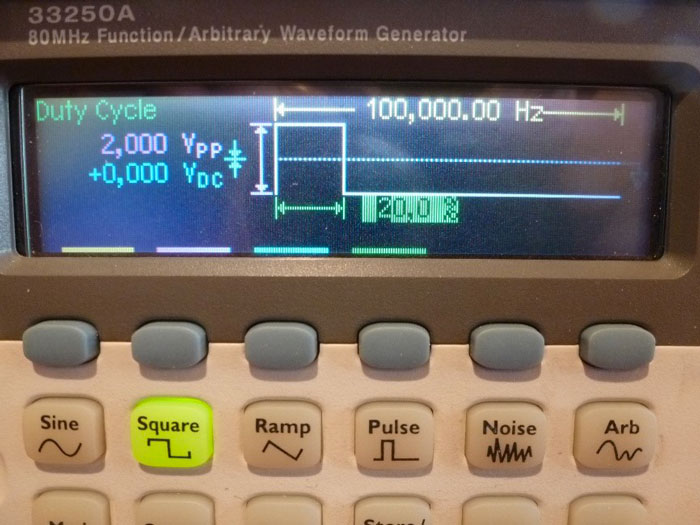
Fig. 41 : Consigne au générateur d’un signal rectangulaire symétrique (100 Hz, 2 Vpp) d’un rapport cyclique de 20 %.
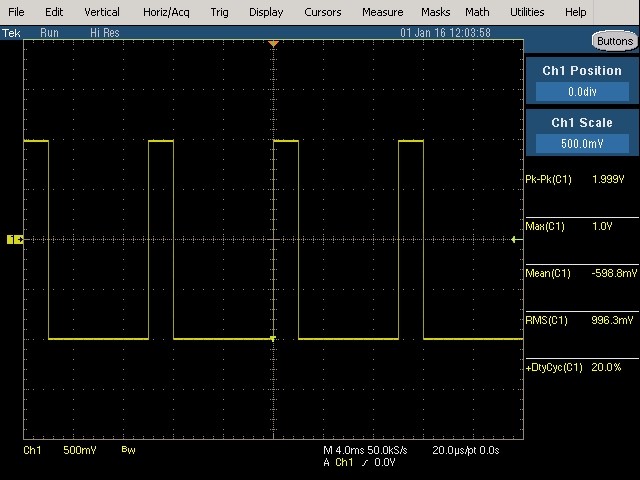
Fig. 42 : Signal rectangulaire symétrique (100 Hz, 2 Vpp) d’un rapport cyclique de 20 %. Mesures de Upp, Upeak, Umoy, URMS (AC+DC), rapport cyclique.
Vérification des mesures décrites ci-dessus pour un signal rectangulaire symétrique dont le rapport cyclique est de 20 %. Les relations mathématiques établies ci-dessus doivent confirmer ces mesures.
Upeak = 1,0 V
Umoy = -598,8 mV ;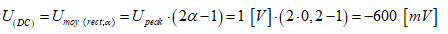
La mesure de Umoy se confirme : -598,8 mV ≈ -600 mV.
URMS (AC+DC) = 996,3 mVRMS ≈ 1 VRMS (= Upeak)
Fig. 43 : Mesures d’un signal rectangulaire symétrique (100 Hz, 2 Vpp) d’un rapport cyclique de 20 %. Mesures de la tension efficace vraie URMS (AC) au moyen d’un voltmètre analogique RMS responding et d’un multimètre True RMS.
Ci-dessus, nous vérifions les mesures de la composante strictement variable d’un signal rectangulaire symétrique dont le rapport cyclique est de 20 %. La relation mathématique de la mesure de U(AC) doit se vérifier.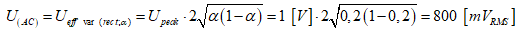
Sur le voltmètre analogique RMS responding, la mesure de U(AC) = 0,8 VRMS.
Sur le multimètre true RMS, la mesure de U(AC) = 801 mVRMS.
Les mesures relevées ci-dessus sont des vraies mesures sur le signal rectangulaire. On remarquera une nouvelle fois la précision redoutable de ces appareils.
Fig. 44 : Mesure de la composante strictement variable (U(AC) à gauche) et mesure de la tension moyenne (U(DC) à droite) pour un signal rectangulaire symétrique (100 Hz, 2 Vpp) d’un rapport cyclique de 20 %.
Ci-dessus, la valeur de la tension moyenne est confirmée avec la mesure en courant continu par le multimètre Fluke 28.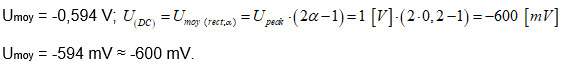
Voici les mêmes mesures que ci-dessus mais réalisées au moyen d’un multimètre étalon de laboratoire HP 3458A permettant de mesurer distinctement les tensions efficaces vraies U(AC+DC), U(AC) et U(DC). Il s’agit de vraies mesures effectuées sur un signal rectangulaire symétrique 100 Hz, 2 Vpp, α = 20 %.
Fig. 45 : Mesure de la tension efficace vraie totale U(AC+DC).URMS (AC+DC) = 999,7 mVRMS ≈ 1 VRMS (= Upeak)
Fig. 46 : Mesure de la tension efficace vraie strictement variable U(AC). URMS (AC) = 800,2 mVRMS ≈ 800 mVRMS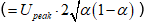 
Fig. 47 : Mesure de la tension moyenne U(DC).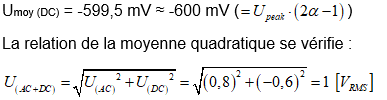
Cas de la mesure de la sinusoïde d’un réseau de distribution d’énergie électrique.
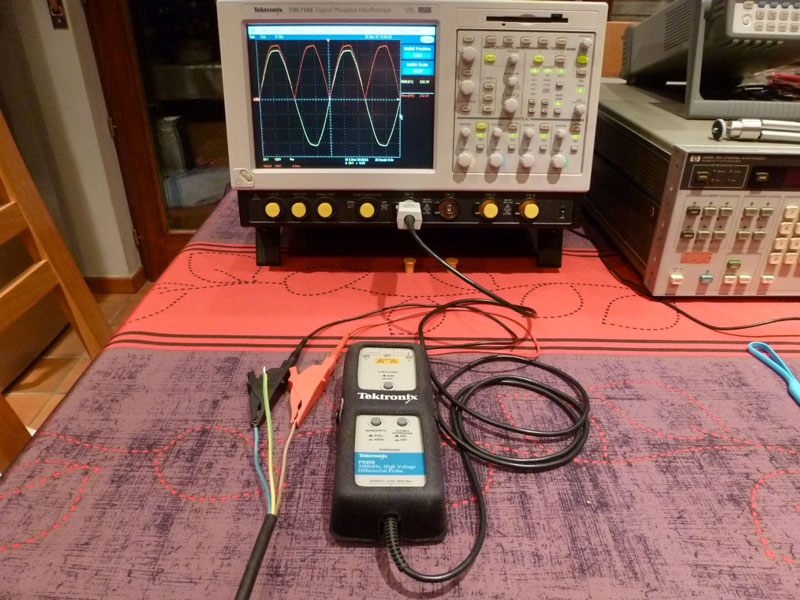
Fig. 48 : Mesure de la valeur RMS du réseau de distribution d’énergie 230 VRMS 50 Hz avec une sonde différentielle haute tension appropriée.
ATTENTION : Ne jamais raccorder l’entrée d’un oscilloscope directement sur le réseau électrique !
En effet, l’entrée de l’oscilloscope a un point commun avec la masse qui est raccordée à la prise de terre (PE : Protection Électrique). Aucune phase du réseau ne doit être raccordée à un point commun avec la masse étant elle-même raccordée au conducteur PE car notre réseau de distribution électrique est du type TT (Terre–Terre). Pour approfondir le sujet de ce type de réseau, nous invitons le lecteur à aller consulter le cahier technique n° 172 rédigé par Schneider Electric (disponible sur Internet). Si une des phases (que cela soit le neutre ou la phase) d’un réseau électrique TT vient en contact avec la terre, cela présente dans l’installation une condition de défaut électrique qui doit faire déclencher un Dispositif Différentiel Résiduel (DDR).
La seule façon de raccorder sur le réseau électrique un appareil de mesure qui a un point commun avec la masse reliée au PE est d’utiliser une sonde différentielle qui ne présente aucun point commun avec la masse. Il est donc exclu d’utiliser une sonde conventionnelle pour oscilloscope qui a un point de raccordement avec la masse.
Fig. 49 : Sonde différentielle haute tension utilisée entre autres pour les mesures sur des réseaux électriques. Il y a lieu de se rappeler qu’une tension efficace de 230 V représente une amplitude crête à crête de 650 Vpp. Il s’agit donc bien de haute tension !
Remarque : pour une mesure en mode différentiel sur un oscilloscope on peut utiliser deux sondes conventionnelles (sans relier la masse de celles-ci). Chaque sonde est raccordée sur un canal de l’oscilloscope dont un des deux canaux est paramétré en inverse du signal. Il suffit d’activer la fonction d’addition des deux canaux pour obtenir la mesure en mode différentiel : Ch1 + Inv (Ch 2) = Ch1 – Ch 2.
Attention : les sondes conventionnelles ont une tension maximale admissible. Les sondes de catégorie II utilisées en électronique admettent en général une tension maximale de 300 V ce qui est insuffisant pour des mesures sur le réseau électrique (on risque de les claquer). Seules les sondes haute tension 1000 V avec un facteur x100 peuvent être raccordées sur le réseau à condition qu’elles soient utilisées par paires en mode différentiel sans raccorder la masse de celles-ci aux phases du réseau.
Le réseau de distribution d’énergie électrique dont nous disposons délivre une tension efficace de 230 V à une fréquence de 50 Hz et est de forme sinusoïdale. Toutefois, la sinusoïde du réseau comporte une légère distorsion comme nous allons l’observer.
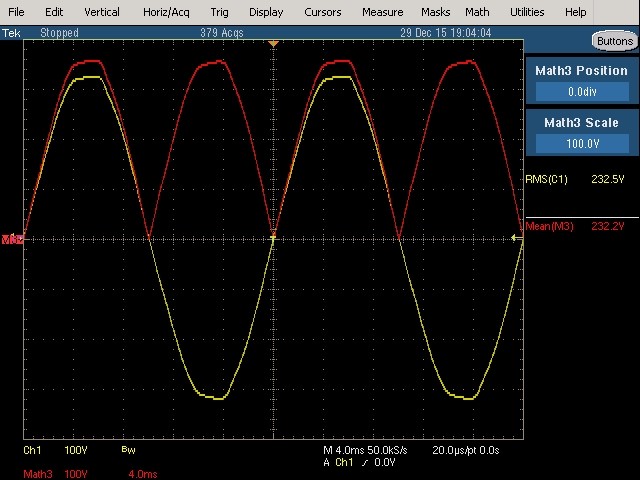
Fig. 50 : Signal sinusoïdal avec légère distorsion d’un réseau de distribution d’énergie électrique d’une tension efficace nominale de 230 V 50 Hz.
Mesure True RMS : 232,5 VRMS.
Cette mesure est confirmée par le multimètre True RMS de chantier Fluke 28 qui est un appareil portable à double isolation et qui ne présente aucun point commun avec la masse. La mesure est donc directement effectuée en mode différentiel. Simulation de mesure RMS average responding à l’oscilloscope : 232,2 VRMS.
Les deux mesures True RMS et RMS average responding sont cohérentes. En effet, la sinusoïde du réseau est presque parfaite et peut donc être mesurée valablement avec un voltmètre RMS average responding sans que l’erreur de mesure ne soit significative.
Dans la dernière expérience, nous allons observer la forme de la tension alternative à la sortie d’un transformateur. Cela va nous réserver quelques surprises !
Nous avons réalisé un montage avec un Variac qui alimente un petit transformateur d’alimentation dont le secondaire transfo est isolé par rapport au réseau électrique. Il n’y a donc aucun danger à réaliser une mesure avec des appareils dont l’entrée présente un point commun avec la masse : le transfo réalise une isolation galvanique par rapport au réseau électrique. Tout se passe comme si un réseau du type IT (Isolé–Terre) avait été recréé avec le transformateur d’isolation galvanique.
Le Variac et le petit transfo ont été montés de manière pratique dans une ancienne carcasse d’appareil trouvé sur le marcher aux puces (HP 8404A Leveling Amplifier)
Fig. 51 : Montage d’un Variac et d’un petit transfo d’isolation galvanique dans une carcasse HP 8404A
Fig. 52 : Montage du Variac sur la face avant de la carcasse.
Fig. 53 : Montage du petit transfo d’isolation galvanique.
Voici le banc de mesure avec l’oscilloscope numérique TEK 7104, un voltmètre analogique RMS HP 400E average responding, un voltmètre analogique RMS HP 3400B RMS responding et un multimètre de chantier True RMS Fluke 28. Les entrées de tous les appareils de mesure sont à haute impédance et sont raccordées en parallèle sur la sortie du secondaire transfo sous test.
Fig. 54 : Banc de mesure pour le relevé d’oscillogramme de la tension de sortie d’un transformateur et mesure de la tension efficace vraie au secondaire transfo.
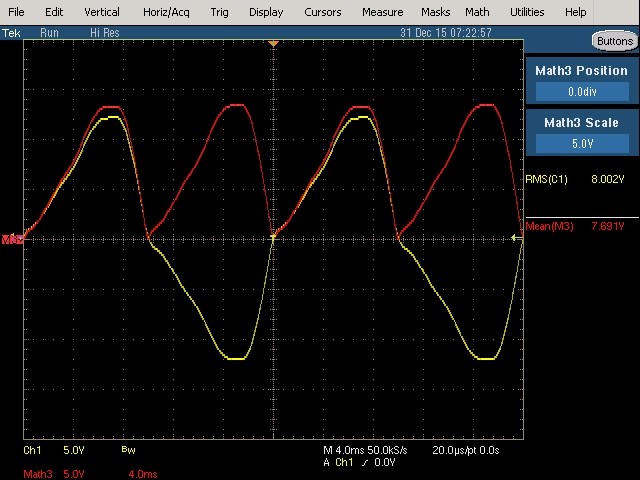
Fig. 55 : Mesure True RMS et average responding de la tension de sortie transfo. Le Variac est réglé vers la position du minimum de tension pour obtenir une tension nominale de 8 VRMS au secondaire transfo.
Mesure de la tension efficace vraie, True RMS : 8,002 VRMS.
Simulation de mesure RMS average responding à l’oscilloscope : 7,691 VRMS. Cette mesure est erronée et on constate que l’erreur est flagrante.
La distorsion de la sinusoïde de la tension de sortie du transfo est suffisante pour fausser la mesure avec un dispositif RMS average responding. Cette distorsion s’explique par la saturation du noyau magnétique du transfo : le nombre de spires du primaire ne sont pas suffisantes et donnent pour résultat une valeur d’ampères–tour trop élevée. Ainsi, l’induction électromagnétique dans le noyau devient trop élevée avec un ordre de grandeur au-delà de 12.000 Gauss (1,2 Tesla). Cette induction trop élevée sature le matériau ferromagnétique du transfo et provoque ainsi une distorsion de la forme du courant alternatif au secondaire du transfo.
Dans la réalité, le nombre de spires du primaire transfo est approprié. Dans notre expérience, nous avons légèrement survolté le primaire du transfo à l’aide du Variac de façon à accentuer le phénomène de saturation du noyau magnétique du transfo.
Les mesures de tension efficace vraie peuvent légèrement fluctuer en fonction de celle de la tension du réseau électrique au cours du temps (le temps de réaliser les clichés).
Fig. 56 : Mesure de la tension secondaire transfo (tension nominale 8 VRMS) sur un voltmètre RMS average responding HP 400E (à gauche) et sur un voltmètre RMS responding HP3400B (à droite). Il y a une légère parallaxe sur la droite du cliché ci-dessus.
Mesure de la tension efficace RMS responding : 8,00 VRMS.
Mesure RMS average responding : 7,75 VRMS (mesure erronée).
Mesure True RMS : 7,98VRMS.
Fig. 57 : Mesure de la tension nominale 8 VRMS secondaire transfo sur un multimètre True RMS
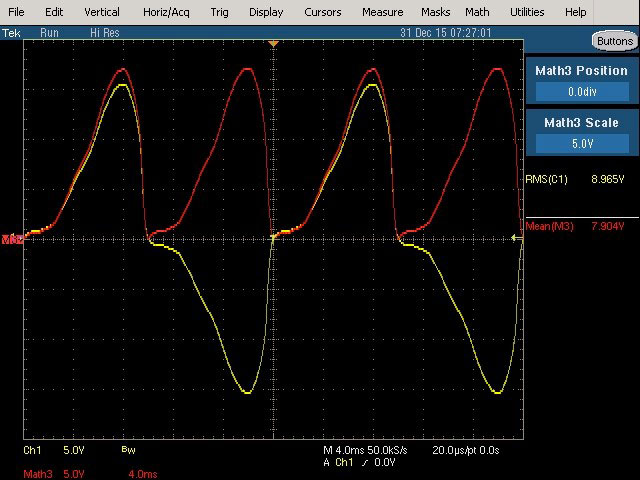
Fig. 58 : Mesure True RMS et average responding de la tension de sortie transfo. Le Variac est réglé vers la position du maximum de tension pour obtenir une tension nominale de 9 VRMS au secondaire transfo.
Mesure de la tension efficace vraie, True RMS : 8,965 VRMS.
Simulation de mesure RMS average responding à l’oscilloscope : 7,904 VRMS. Cette mesure est erronée et on constate que l’erreur est encore accentuée.
La distorsion de la sinusoïde de la tension de sortie du transfo est plus importante car la saturation du noyau du transfo a augmenté et accentue le phénomène de distorsion.
Fig. 60 : Mesure de la tension nominale de 9 V au secondaire transfo sur un multimètre True RMS.
En conclusion de toutes les expériences qui ont été réalisées, Il y a lieu de bien retenir que les mesures des tensions alternatives sont délicates lorsqu’elles sont effectuées sur un voltmètre conventionnel qui n’est pas certifié True RMS ou RMS responding. En effet, la plupart de ces voltmètres effectuent des mesures RMS average responding et sont donc de facto dépendantes de la pureté de la sinusoïde du signal mesuré.
Un exemple particulièrement critique de mesure est celle qui est effectuée à la sortie du secondaire d’un transformateur devant alimenter le filament d’un tube radiofréquence d’un amplificateur linéaire de forte puissance. Nombreux sont les radioamateurs qui ont expérimenté des amplificateurs linéaires avec des tubes 2C39A, 4X150A, 4CX250B, 3CX1500A7, 4CX1000, 3-500Z, 3-1000Z, GU78B, ou autres QB4-1100, etc. Tous ces tubes radio doivent avoir une tension d’alimentation du filament rigoureusement exacte et précise. Si la valeur de tension filament est par défaut ou par excès, la durée de vie du tube est considérablement écourtée.
L’explication est simple à comprendre : le but du filament est de chauffer la cathode pour provoquer une agitation thermoïonique et créer une charge d’espace d’électrons. Parfois, la cathode est à chauffage direct : le filament est la cathode. Celle-ci doit être à une température optimale pour bénéficier des propriétés émissives d’électrons sans vieillissement prématuré de cette cathode. En effet, dans un tube radio de puissance, l’anode « arrache » littéralement les électrons de la cathode.
Rappelons-nous la définition d’une tension efficace : valeur de tension continue qui apporterait une même dissipation de puissance que celle qui est apportée par la tension alternative du signal à mesurer si elle était appliquée à une même résistance. Ici, la résistance est le filament et la puissance dissipée dans celui-ci est créée par effet Joules pour porter le filament à une température optimale.
On comprend mieux à présent que la mesure de tension filament doit être effectuée par un voltmètre True RMS car la forme de la tension à ses bornes a subit la distorsion de la sinusoïde du réseau électrique et surtout celle du transformateur d’alimentation.
Fig. 61 : Voici les vieux multimètres poussiéreux qui appartenaient à grand-papa. Ces voltmètres ne sont pas True RMS mais sont tous du type average responding. Attention à ce que l’on mesure, ou ce que l’on croit mesurer.
Cet article peut être téléchargé au format PDF. Il suffit de cliquer sur ce lien :
A propos de l'auteur
