Introduction :

Alimenter un transceiver d’une station de radioamateur peut paraître une chose simple à réaliser et ne doit en principe poser aucune difficulté à un OM.  Toutefois la manière d’agencer la mise à disposition de l’énergie électrique nécessaire à un transceiver requiert un certain savoir-faire dans la pratique lorsque la station radio doit être fonctionnelle en toutes circonstances, c’est-à-dire non seulement dans le shack, mais aussi en station mobile ou en station portable, par exemple lors d’un exercice B-EARS (Belgian Emergency Radio Service) ou lors d’un Fielday.

Ce quiz m’a été suggéré par Paul ON6DP pour que je propose la rédaction d’un article technique à ce sujet sur le site Internet des radioamateurs de Liège ON5VL.  Dans cet article, nous partons de situations concrètes où l’on va adopter une approche méthodologique, étape par étape, et avec quelques calculs très simples qui sont abordables par tous.  Les résultats seront très orientés vers la pratique.

Une première situation concrète dans un shack où ça marche mais de temps en temps avec des problèmes, pourquoi ?

Quiz n° 1

J’ai un transceiver ondes courtes qui est alimenté sous une tension de 13,8 V par l’intermédiaire d’une alimentation secteur à découpage et de haut rendement.  L’alimentation peut délivrer un courant maximal de 82 A.  À pleine puissance d’émission, l’intensité du courant qui circule entre l’alimentation et le transceiver est de 45 A.  Le transceiver dispose de deux connecteurs d’entrées d’alimentation commune, ce qui permet de le raccorder par deux faisceaux de câbles distincts à une sortie commune de l’alimentation.  Les câbles que j’utilise ont une section des conducteurs de AWG 12.  Le premier câble a une longueur de 3 m et le second câble a une longueur de 2 m.  Chaque câble est protégé respectivement par deux fusibles de 25 A : un sur le pôle positif et un sur le pôle négatif ; il y a donc quatre fusibles en tout.  De temps en temps, il y a un des deux fusibles de 25 A qui claque (toujours sur la même branche).  Je constate aussi que les câbles ont tendance à beaucoup chauffer.

Questions :

• Pourquoi les câbles chauffent-ils beaucoup ?
• Pourquoi un des deux fusibles finit toujours par claquer sur la même branche ?
• Que faut-il faire pour remédier à la situation ?

Ces questions peuvent paraître anodines, mais il y a toute une physique de l’électricité qui se cache là derrière et que nous vous proposons de découvrir ou de redécouvrir avec une méthode analytique.

Réponses et explications au quiz n° 1 :

Table de conversion des sections de conducteurs données en AWG (American Wire Gauge) vers le système métrique :

En électronique, la section des conducteurs est parfois donnée en jauge AWG, ce qui est usuel dans les publications des radioamateurs américains, comme par exemple dans l’ARRL Radioamateur’s Handbook.  Ces jauges sont d’application aux fils de bobinage (fils de cuivre émaillés) et aux fils de câblage (fils rigides monobrin ou fils souples multibrins avec une isolation en matériau synthétique, par exemple PVC).

Le plus simple pour convertir une jauge AWG vers le système métrique est de consulter un tableau qui donne la correspondance entre le numéro de la jauge et le diamètre du fil en mm ou la section du fil en mm².  Ce qu’il faut retenir, c’est que plus le numéro de la jauge est de valeur élevée et plus la section du fil est de faible valeur.

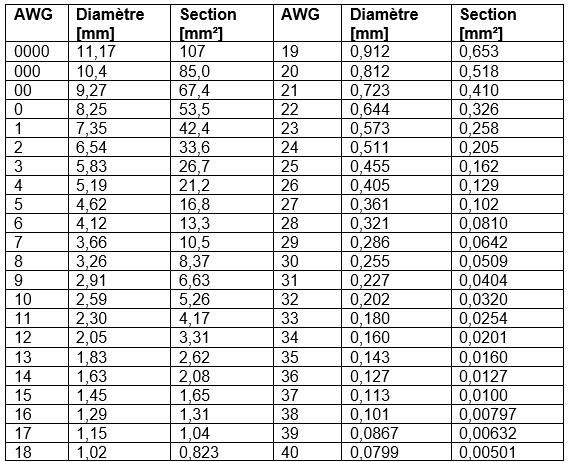
Dans notre exemple, un conducteur de AWG 12 a un diamètre de 2,05 mm et une section de 3,31 mm².  La mesure du diamètre d’un fil est aisée au moyen d’un pied à coulisse.  La connaissance de la section permet d’évaluer si un conducteur électrique est adapté à une application bien définie, en particulier au point de vue de l’intensité du courant qui doit traverser ce conducteur.

Échauffement d’un conducteur :

L’échauffement d’un conducteur électrique en courant continu est dû aux pertes par effet Joule car le conducteur offre une résistance au passage du courant.  Les pertes par effet Joule sont directement proportionnelles à la résistance du conducteur et sont proportionnelles au carré du courant qui le traverse.

P_J = R.I²

P_J : perte par effet Joule [W]

R : résistance du conducteur [Ω]

I : courant traversant le conducteur [A]

Les pertes par effet Joule ont pour effet de dissiper une quantité de chaleur par unité de temps dans le conducteur ; il s’agit bien d’une puissance, c’est-à-dire une quantité d’énergie par unité de temps exprimée en Joules par seconde ou en kilocalorie par seconde.

1 kcal = 4186,8 J

1 KJ = 0,2388 Kcal

La quantité de chaleur qui est produite au cours du temps dans le conducteur aura pour effet une élévation de la température de celui-ci.  Au départ, en l’absence de courant, le cuivre du conducteur est à la température ambiante de l’environnement dans lequel il se trouve et au moment où il s’y trouve.  Lors de l’établissement du passage du courant, l’énergie dissipée (la quantité de chaleur produite) échauffe la masse de cuivre du conducteur et la température augmente.  En d’autres mots, l’écart de température augmente entre celle du cuivre et celle de l’environnement qui reste à une température que l’on peut considérer pratiquement comme constante.  La quantité de chaleur qui contribue uniquement à l’élévation de la température de la masse de cuivre est donnée par la relation suivante.

Ceci explique qu’il faut un certain temps pour réchauffer toute la masse de cuivre du conducteur à une certaine température (en supposant pour l’instant que le conducteur n’est pas encore refroidi par le milieu ambiant).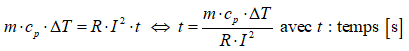

Il arrive un moment où la masse de cuivre atteint une température d’équilibre car l’environnement du conducteur refroidit celui-ci en fonction de l’écart de température entre le conducteur et son environnement.  À la température d’équilibre, la chaleur produite par unité de temps par le courant traversant le conducteur (puissance dissipée par effet Joule) équivaut la quantité de chaleur qui est échangée par unité de temps avec le milieu ambiant.  Cet échange de chaleur avec le milieu ambiant s’effectue par rayonnement infra-rouge, par conduction entre le cuivre et le milieu ambiant et par les connexions du conducteur à ses extrémités, et enfin essentiellement par convection de l’air qui est brassé autour du conducteur.

La modélisation mathématique de l’échange de chaleur d’un conducteur avec son milieu ambiant est relativement complexe à établir car elle est fonction de plusieurs paramètres.  Ces paramètres peuvent être regroupés sous le format d’un coefficient qui est établi en fonction des conditions physiques pratiques dans lequel le conducteur se situe.  On doit donc évaluer le mode d’installation du conducteur, par exemple :

• Conducteur simple placé à l’air libre sur des isolateurs (lignes électriques extérieurs) ;
• Conducteur placé dans un câble comprenant plusieurs conducteurs en charge ;
• Câble posé à l’air libre sur une surface (mur, sol) ;
• Câble posé dans des gaines enfouies (encastrement dans des murs, enfouissement dans le sol) ;
• Câble posé sur des chemins de câble en présence d’autres câbles en charge ;
• Fil conducteur d’un bobinage d’enroulement de transformateur, etc.

Dans le cas d’un conducteur simple placé à l’air libre, on peut modéliser l’échange de chaleur avec le milieu ambiant selon la relation suivante.

On peut retenir que l’échange de chaleur est directement proportionnel à la surface de contact entre le conducteur et son milieu ambiant, directement proportionnel à l’écart de température et directement proportionnel au coefficient d’échange de chaleur.  Ce coefficient d’échange de chaleur peut être interprété et comparé à l’inverse d’une résistance thermique entre le conducteur et le milieu ambiant (conductibilité thermique).

La proportionnalité de l’échange de chaleur avec l’écart de température explique que le conducteur atteint une température d’équilibre où l’on obtient l’équivalence entre les pertes Joule et l’échange de chaleur avec le milieu ambiant par unité de temps.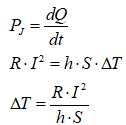

Que faire avec une telle relation mathématique ?  Où nous voulons en venir, c’est de déterminer le paramètre critique qui est le principal responsable de l’échauffement d’un conducteur électrique pour que celui-ci ne dépasse pas une température excessive.  Il y a donc lieu d’aller un peu plus loin dans le raisonnement afin de trouver le critère sur lequel on se base pour déterminer la section optimale d’un conducteur électrique pour que celui-ci subisse un échauffement acceptable pour un courant donné et pour des conditions d’installation données.

Pour continuer le raisonnement, on va faire appel à deux relations mathématiques qui caractérisent d’une part le calcul de la résistance d’un conducteur électrique et d’autre part le calcul de la répartition du courant dans la section d’un conducteur électrique.

Résistance d’un conducteur (loi de Pouillet) :

En substituant la résistance et la densité de courant dans l’équation de l’écart de température on obtient ce qui suit.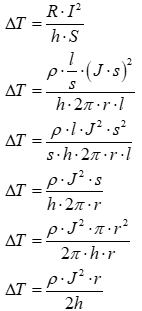

On constate que l’échauffement d’un conducteur est indépendant de la longueur de celui-ci.

On constate aussi que l’échauffement d’un conducteur d’une section donnée (et donc de rayon de section circulaire constant) est uniquement fonction du carré de la densité de courant.  En effet, la résistivité (ρ) est une constante et le coefficient d’échange de chaleur (h) est aussi une constante.

Il est donc important de retenir que la section d’un conducteur est déterminée par la densité de courant maximale admissible pour que l’échauffement de ce conducteur soit acceptable dans les conditions de son installation.

Il y a toutefois un dernier élément dont il faut tenir compte.  Pour un conducteur d’une longueur donnée (constante) et pour une densité de courant donnée, la section du conducteur est proportionnelle au courant qui doit le traverser.  Or un volume est le cube d’une longueur et la surface est le carré d’une longueur.  En d’autres mots, le volume d’un conducteur croît plus vite que celui de sa surface de contact avec l’air ambiant pour le refroidir.  Ainsi, il est usuel d’admettre une densité de courant maximale qui doit avoir une valeur réduite pour des conducteurs de section circulaire élevée (fortes sections).  C’est aussi la raison pour laquelle les conducteurs devant faire circuler une intensité de valeur extrêmement élevée prennent la forme de barres de section rectangulaire pour offrir un maximum de surface d’échange avec l’air ambiant pour le refroidissement (jeux de barres des tableaux électriques).

On peut se baser sur la formule empirique suivante pour le calcul du courant maximum admissible dans une section de conducteur normalisé composant un câble d’installation électrique.

I = 11 .  S^0,625

I : courant maximum admissible dans un conducteur d'un câble (installation domestique) [A]

s : section du conducteur [mm²]

Voici un tableau avec les valeurs de courant admissible et les valeurs de densité de courant admissible en fonction des sections normalisées des conducteurs usuels.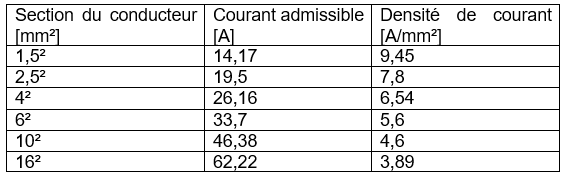

Dans la pratique, pour le raccordement d’un transceiver en basse tension (13,8 V) et donc pour des courants d’intensités élevées de l’ordre de 25 A à 50 A, on choisira une densité de courant maximale comprise entre 4 A/mm² et 6 A/mm².

Dans notre exemple du quiz n° 1, les conducteurs pour chaque faisceau des deux câbles en parallèle doivent se répartir un courant d’une intensité de 45 A, ce qui donne en première approximation une valeur de l’ordre de 22,5 A par câble (pour autant que ceux-ci aient la même longueur et donc la même résistance).  En choisissant une section idéale de 6 mm², on aurait une densité de courant de 3,75 A.  En choisissant une section de 4 mm², on obtient une densité de courant de 5,625 A/mm², ce qui constitue un compromis acceptable.  En câblant deux conducteurs de 2,5 mm² en parallèle pour chaque conducteur de chaque câble, on obtient une section de 5 mm² et une densité de courant de 4,5 A, ce qui est une valeur tout-à-fait correcte.

Pour un conducteur d’une section de AWG12 (3,31 mm²) et pour un courant de 22,5 A on arrive à une densité de courant de 6,8 A/mm² ; cette valeur devient relativement élevée et explique l’échauffement prononcé des conducteurs traversés chacun par un courant de 22,5 A.

Chute de tension dans les conducteurs et déséquilibre de courant dans des conducteurs placés en parallèle :

La chute de tension dans un conducteur est directement proportionnelle au courant qui le traverse et est directement proportionnelle à la résistance linéique du conducteur.

U = R.I ; loi d'Ohm

R = ρ. l/s ; loi de Pouillet

La résistivité du cuivre à température ambiante (27 °C ou 300 K) a pour valeur :

ρ_cu = 17. ^10-9 [Ω.m]

Il est usuel de donner la résistance linéique d’un conducteur en Ω.mm²/m, ce qui correspond à 10^-6 Ω.m ou bien en Ω.mm²/km, ce qui correspond à 10^-9 Ω.m.

Par exemple, un conducteur d’une section de AWG 12 a une résistance linéique de 5,21 Ω/km (pour une section de 3,31 mm²), ce qui correspond à une résistance linéique de 5,21 mΩ/m.  On peut vérifier cette valeur par la loi de Pouillet :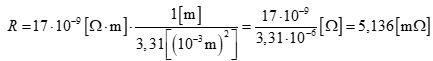

La différence de résultat s’explique par le fait que la donnée de la résistance linéique d’un conducteur AWG 12 a été donnée à une autre température que 300 K.
En prenant une résistivité de 5,21 mΩ/m pour un conducteur de section AWG 12, la résistance d’un conducteur AWG 12 de 2 m est de R₁ = 10,42 mΩ et pour un conducteur AWG 12 de 3 m est de R₂ = 15,63 mΩ.

Si deux conducteurs de résistances différentes sont placés en parallèle, alors on obtient un déséquilibre de courant entre ces deux conducteurs.

Voici comment se présente le schéma-bloc du raccordement du transceiver :

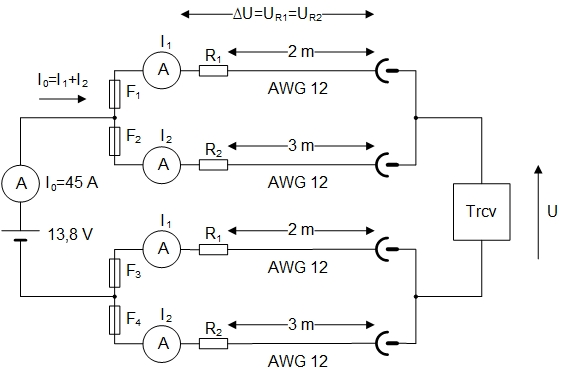
Fig. 1 : Schéma-bloc d’un transceiver alimenté par deux faisceaux de câbles constitués de conducteurs de section AWG 12 ; le 1^er faisceau a une longueur de 2 m et le 2^ème a une longueur de 3 m.  Graphisme : ON4IJ.

On peut établir deux relations mathématiques sur la répartition des courants et des tensions selon les lois de Kirchhoff : loi des nœuds et loi des mailles.

I₀ = I₁ + I₂

ΔU = U_R1 = U_R2 

En appliquant la loi d'Ohm, on obtient :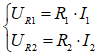

En combinant les trois équations ci-dessus, on obtient :

On peut à présent calculer la chute de tension entre les bornes de l’alimentation et celles du tranceiver.  Soit on calcule la résistance équivalente du circuit qui est R_eq = 2 x (R₁//R2) et que l’on multiplie par I₀, soit on calcule la tension ∆U_tot = 2 x U_R1 = 2 x U_R2 = 2 x R₁ x I₁ = 2 x R₂ x I₂.  On doit tenir compte de deux fois la chute de tension dans les conducteurs des câbles : une première fois pour l’aller et une seconde fois pour le retour du courant vers la source de tension.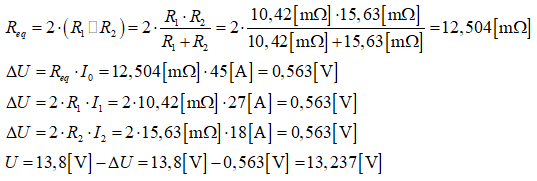

Le transceiver, après une chute de tension de 0,563 V dans le circuit de câbles ne recevra plus qu’une tension de 13,237 V.

Calibre des fusibles :

Les deux câbles entre l’alimentation et le transceiver sont protégés respectivement par deux fusibles (d’une part F₁ et F₂ et d’autre part F₃ et F₄).  Les quatre fusibles ont un calibre de 25 A.  On a calculé le déséquilibre de courant et nous avons constaté qu’il y a un courant de I₁ = 27 A dans une des deux branches du circuit et un courant I₂ = 18 A dans l’autre branche.  Comment se fait-il que le fusible F₁ ou F₃ finit toujours par claquer et que les fusibles F₂ et F₄ ne claquent jamais ?

La réponse peut sembler évidente si l’on se contente de dire que le courant de 27 A excède le calibre de 25 A des fusibles F₁ et F₃.  La réponse est moins évidente si l’on doit expliquer pourquoi un fusible de 25 A ne claque pas tout de suite avec un courant de 27 A.

Un fusible est caractérisé par deux courbes : la courbe de non-fusion et la courbe de fusion qui sont tracées sur un graphique dont l’axe des abscisses représente le courant qui traverse le fusible et dont l’axe des ordonnées représente le temps.

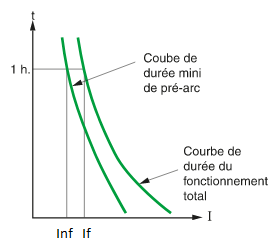
Fig. 2 : Courbes du temps de non-fusion et temps de fusion d’un fusible en fonction du courant qui le traverse.  Source : Guide de l’installation électrique, fr.electrical-installation.org, Installation Électrique, chapitre H, les fusibles.

Sur la figure ci-dessus, la courbe de gauche caractérise le temps de la durée minimale de pré-arc (durée avant le moment de fusion) en fonction de l’intensité qui traverse le fusible et la courbe de droite représente le temps de la durée de fonctionnement total, en d’autres mots la durée totale pour obtenir la coupure du courant (somme de la durée de pré-arc et de la durée de l’arc jusqu’à son extinction).

Le courant conventionnel de non-fusion Inf est la valeur de l’intensité du courant que peut supporter le fusible pendant un temps normalisé de 1 heure sans fondre.  Le courant conventionnel de fusion If est la valeur de l’intensité du courant qui provoque la fusion du fusible avant l’expiration du temps normalisé de 1 heure.

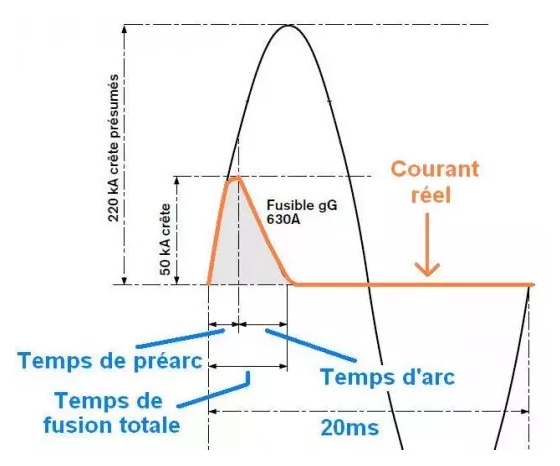
Fig.3 : Chronogramme illustrant le temps de pré-arc, le temps d’arc et le temps de fusion totale d’un fusible placé dans un circuit à courant alternatif.  Source : astuces-pratiques.fr, fusibles.

Un fusible est un dispositif de protection des lignes électriques lorsqu’intervient un défaut sur celles-ci.  Le défaut sur la ligne peut être de deux natures : défaut par court-circuit sur la ligne électrique ou défaut par surcharge de la ligne par un courant excessif.

Pour un calibre donné d’un fusible, la caractéristique temps-courant de fusion doit se situer entre les deux courbes de non-fusion et de fusion.  En pratique, pour deux fusibles différents mais du même calibre et du même type, ces deux fusibles peuvent avoir un temps de fusion total relativement différent l’un de l’autre en particulier pour des courants de surcharge de valeurs légèrement situées au-delà de celle du calibre.

Ainsi, ceci explique qu’un fusible d’un calibre de 25 A peut supporter un courant de surcharge de 27 A parfois pendant plusieurs heures avant de finir par claquer.

Améliorations des connexions entre l’alimentation 13,8 V et le transceiver :

La première action qui s’impose pour la situation du quiz n° 1 est de fabriquer deux nouveaux faisceaux de câbles de longueurs rigoureusement identiques et qui doivent être constitués de conducteurs dont la section est appropriée pour maintenir la densité de courant dans les valeurs recommandées et décrites ci-dessus.

Il y a lieu d’utiliser des câbles dont la longueur est celle qui est strictement nécessaire.  Au plus courts sont les câbles (dans la mesure du possible) et plus la chute de tension sera faible dans les conducteurs.

Il y a moyen de profiter des multiples points de connexions (pins) d’un connecteur qui sont reliés à un même potentiel afin de diminuer les résistances de contact : chaque résistance de contact se met en parallèle l’une sur l’autre.  Ainsi, deux pins raccordées en parallèle au même potentiel offrent une résistance de contact qui est réduite de moitié.

Parfois, les pins d’un connecteur ne peuvent pas accepter des conducteurs de forte section.  En revanche ces connecteurs peuvent disposer de quatre pins : deux pour le pôle positif et deux pour le pôle négatif.  C’est l’opportunité de constituer un faisceau de câble avec des conducteurs de section moyenne mais qui sont redoublés.  Par exemple, il vaut mieux utiliser deux conducteurs d’une section de 2,5 mm² en parallèle constituant une section totale de 2 x 2,5 mm² = 5 mm² à la place d’un seul conducteur de jauge AWG 12 qui a une section de 3,31 mm² à lui seul.  Si les pins des connecteurs peuvent accepter une section de conducteur de 4 mm², alors les câbles seront bien à l’abris de tout échauffement et on bénéficiera principalement d’une moindre chute de tension dans les câbles.  La chute de tension est particulièrement critique pour des alimentations à basse tension (13,8 V) et à courant forts (45 A).

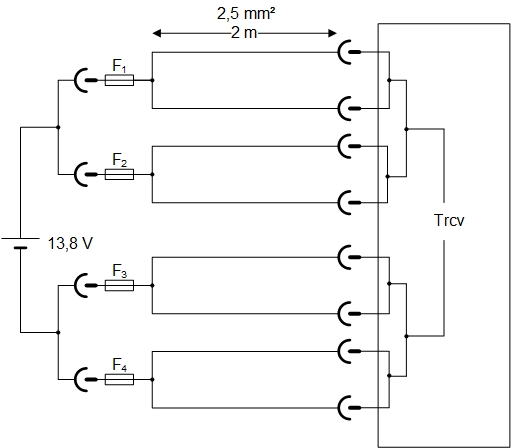
Fig.4 : Solution préconisée en réponse au quiz n° 1.  Graphisme : ON4IJ.

On invite le lecteur à calculer la résistance équivalente du câblage selon la figure ci-dessus avec des conducteurs redoublés d’une section de 2,5 mm² et d’en déduire la chute de tension dans ce type de raccordement.  On peut aussi faire l’exercice avec des conducteurs d’une section de 4 mm².  Les résultats seront comparés à ceux qui ont été calculés précédemment ci-dessus avec des conducteurs d’une section AWG 12.

Quiz n° 2

Je dois organiser, pour un Fielday de 24 heures, l’alimentation d’un transceiver VHF en portable à partir d’une batterie 12 V et d’un panneau photovoltaïque d’une puissance de 300 W crête.  Le panneau photovoltaïque recharge la batterie par l’intermédiaire d’un régulateur qui interface la tension de sortie du panneau solaire avec la tension de charge de la batterie.  Le rendement du régulateur de tension pour le panneau solaire est de 85 %.  La tension 12 V de la batterie alimente un élévateur de tension vers 13,8 V pour alimenter le transceiver VHF.  Le rendement de l’élévateur de tension 12 V vers 13,8 V est de 90 %.  Sous une tension de 13,8 V, le transceiver consomme un courant de 15 A à pleine puissance d’émission et consomme un courant de 2 A lorsqu’il est en réception.  J’estime que la durée d’émission devrait être de 60 % du temps et que la durée de réception est de 40 % du temps au cours des 24 heures.  On annonce une météo favorable pour la date du Fielday avec un temps relativement bien ensoleillé pour un mois de juin.  Le Fielday commence à 10 h 00 du matin et se termine le lendemain à la même heure.  On annonce le lever du soleil à 05h20 du matin et le coucher à 21h50.  Toutefois, l’ensoleillement effectif moyen est de 9 heures en Belgique au mois de juin avec une moyenne d’intensité lumineuse de 75 % de l’intensité maximale de la journée établie sur un ensoleillement effectif de 9 heures.  On suppose que le panneau photovoltaïque sera toujours orienté de façon optimale par rapport à la direction du soleil et que l’opérateur de la station radio corrigera l’orientation du panneau solaire au cours de la journée.

Questions :

• Quel est le bilan de consommation énergétique de la station radio du Fielday ?
• Quelle capacité de batterie faut-il prévoir sans l’apport énergétique du panneau photovoltaïque ?
• Quel est le bilan énergétique apporté par le panneau photovoltaïque ?
• Quelle capacité de batterie faut-il prévoir sachant que celle-ci bénéficie de l’apport énergétique amené par le panneau photovoltaïque ?

Réponses et explications au quiz n° 2 :

Bilan de consommation énergétique de la station radio :

Pour établir le bilan énergétique de la station radio, on va commencer par le calcul de la puissance d’alimentation du tranceiver en émission et puis en réception sous une tension de 13,8 V.  Ensuite, on va traduire cette puissance en énergie consommée selon les périodes d’émission et de réception au cours des 24 heures du Fielday.  Enfin, on tiendra compte du rendement de l’élévateur de tension de 12 V vers 13,8 V pour introduire le début du calcul de la capacité de la batterie 12 V qu’il faudra prévoir sans l’apport d’énergie du panneau photovoltaïque.

P_TX = U_TX . I_TX = 13,8[V] . 15[A] = 207 [W]

P_RX = U_RX . I_RX = 13,8[V] . 2[A] = 27,6[W]

Dans une heure il y a 60 minutes et dans une minute il y a 60 secondes.  Dans une heure il y a donc 60 secondes par minutes x 60 minutes = 3600 secondes par heure.  Sur une période de 24 heures, il y a 24 heures x 3600 secondes par heure, ce qui donne 86400 secondes.

100 % du temps du Fielday donne 86 400 secondes ;
1 % du temps du Fielday donne 86 400 secondes divisé par 100, ce qui donne 864 secondes ;
60 % du temps du Fielday en émission donne 864 secondes multiplié par 60, ce qui donne t_TX = 51 840 secondes ;
40 % du temps du Fielday en réception donne 864 secondes multiplié par 40, ce qui donne t_RX = 34 560 secondes.

Énergie consommée par la station radio sur une période de 24 heures (en unités S.I. : Système International mksA) :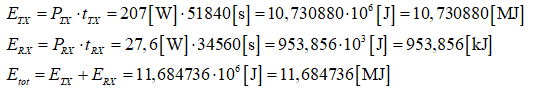

Pour mieux se représenter cette quantité d’énergie, on va convertir les Joules en kilo Watt x heure [kWh].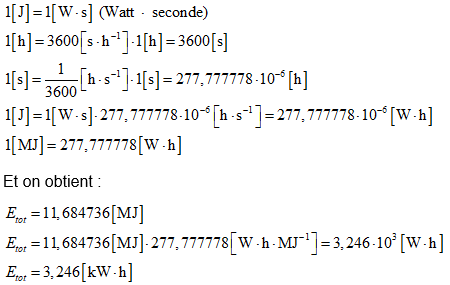

La consommation d’énergie de la station radio sur la période de 24 heures sera donc de 3,246 [kWh].

Définition du rendement en électricité et en électronique :

Le rendement (η) est le rapport entre la puissance de sortie d’un dispositif et la puissance d’entrée de ce dispositif.

Le rendement de l’élévateur de tension 12 V vers 13,8 V est de 90 %.  On va donc pouvoir calculer l’énergie totale qui sera consommée à partir de la batterie 12 V.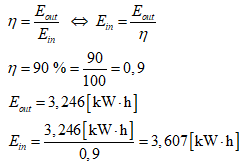

Capacité de la batterie sans apport énergétique du panneau photovoltaïque :

L’énergie que va devoir fournir la batterie pendant la période de 24 heures est de 3,607 kWh.  Nous allons à présent déterminer la capacité de la batterie qui s’exprime en ampère x heure [Ah].

C’est ici qu’il ne faut pas confondre l’unité de capacité d’une batterie, c’est-à-dire une énergie exprimée en Ah ou en kWh (ou en Joules) avec l’unité de l’intensité du courant qui s’exprime en Ampère.

L’énergie, en unité kWh, exprime une puissance en kW multipliée par une unité de temps (ici : 1 heure).  On peut exprimer la partie puissance par le produit d’une tension et d’un courant.  La tension de la batterie étant de 12 V, on peut calculer le courant que la batterie devrait délivrer comme si elle devait fournir toute l’énergie consommée pendant 24 heures en seulement 1 heure (unité de temps).  En effet, une énergie de 3,607 kWh correspond à une puissance de 3,607 kW pendant 1 heure (unité de temps).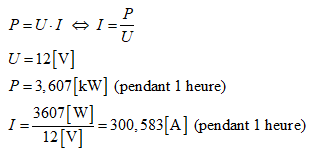

La capacité de la batterie doit donc être (sans apport d’énergie du panneau photovoltaïque) de 300,583 Ampères pendant 1 heure, c’est-à-dire 300,583 Ah.

Quelle sera l’intensité moyenne que devra fournir la batterie pendant 24 heures ?

Quelle sera l’intensité de pointe à la sortie de la batterie lors d’une période d’émission à pleine puissance ?
Pour effectuer ce calcul, il est plus simple de démarrer à partir de la puissance consommée par le transceiver en émission sous une tension de 13,8 V et de tenir compte du rendement de l’élévateur de tension de 12 V vers 13,8 V.  Ensuite, à partir de la puissance de pointe fournie par la batterie sous une tension de 12 V, on pourra calculer le courant de pointe fourni par la batterie.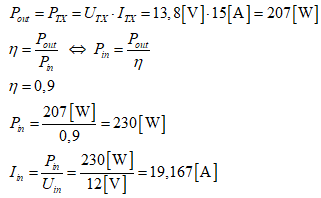

En ce qui concerne une batterie, il ne faut pas confondre sa capacité en Ah avec le courant maximum de crête que peut délivrer une batterie (en général pendant un temps très court).  Il est intéressant de connaître le courant maximum de crête d’une batterie lorsque celle-ci doit alimenter le démarreur d’un moteur thermique.  En effet, un démarreur nécessite un appel de courant très élevé à la batterie lors du démarrage d’un moteur thermique (véhicule automobile par exemple).

Bilan énergétique apporté par le panneau photovoltaïque :

Le calcul de l’énergie apportée par un panneau photovoltaïque est relativement complexe.  Ici, nous proposons une méthode très simplifiée qui comporte quelques raccourcis dans l’énoncé du quiz n° 2.

Dans l’énoncé, nous avons volontairement donné des informations « inutiles » de façon à ce qu’on puisse porter un regard critique sur les données qui sont pertinentes et celles qui sont superflues.  Par exemple, peu importe l’heure du lever et l’heure du coucher du soleil.  En effet, même si le soleil est déjà levé au mois de juin à 5h20 du matin et que le Fielday ne commence qu’à 10h00 du matin, la période d’ensoleillement dont on n’a pas pu profiter entre 05h20 et 10h00 du premier jour sera bien présente le lendemain entre les mêmes heures à la fin du Fielday.  La seule information utile est celle de la durée moyenne exploitable pour des panneaux photovoltaïques en une journée qui est de 9 heures en Belgique et au mois de juin.  En outre, l’intensité lumineuse varie au cours de la journée pour atteindre un maximum lorsque le soleil est au zénith et que la trajectoire des rayons lumineux est la plus courte dans l’atmosphère (minimum d’atténuation).  C’est la raison pour laquelle on donne une intensité lumineuse moyenne de 75 % sur la période exploitable de 9 heures pour une journée en juin.  On peut en déduire que le maximum d’intensité lumineuse au mois de juin qui se situe directement autour de la date du solstice d’été doit correspondre à un maximum de 100 % de la puissance de crête du panneau photovoltaïque (300 W crête).

Ainsi, dans les conditions qui viennent d’être décrites, on peut en déduire que le panneau photovoltaïque va délivrer une puissance de 75 % de 300 W crête pendant 9 heures sur toute la durée du Fielday.

Le bilan de l’énergie apportée par le panneau solaire est :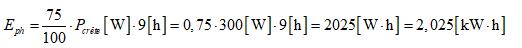

En tenant compte du rendement de 85 % du régulateur de tension placé entre le panneau solaire et la batterie, l’apport en énergie à la batterie par le panneau solaire sera de :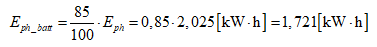

Il reste à convertir cette quantité d’énergie exprimé en kWh en termes de capacité de charge en Ah pour la batterie.

Pour une batterie au plomb, la tension de charge est de 2,35 V par élément, ce qui donne une tension de charge de 14,1 V pour une batterie de 12 V.  En partant de la puissance de charge pendant une unité de temps (1 heure), on peut en déduire un courant de charge comme si toute l’énergie était emmagasinée en 1 heure dans la batterie.

On peut en déduire que sur toute la durée du Fielday, le panneau solaire va apporter une capacité de charge de 122,06 Ah à la batterie.

Quel est le courant de charge de la batterie lorsque le panneau solaire délivre une puissance de 300 W crête lorsque le soleil est au zénith au mois de juin ?

En tenant compte du rendement de 85 % du régulateur de charge entre le panneau solaire et la batterie, on a :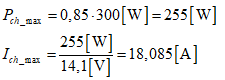

Capacité de la batterie à prévoir en tenant compte de l’apport énergétique du panneau photovoltaïque :

Sans panneau solaire, il faut prévoir une batterie de 300,583 Ah.  Le panneau solaire va apporter une capacité de charge de 122,06 Ah.  Ainsi, il faudra prévoir en final une batterie de 300,583 Ah - 122,06 Ah = 178,52 Ah.  On prendra une batterie dont la capacité a une valeur normalisée immédiatement supérieure à cette valeur : par exemple une batterie de 200 Ah.  Cette batterie sera moins coûteuse et moins lourde qu’une batterie de 300 Ah qu’il aurait fallu prévoir en l’absence du bénéfice de l’énergie apportée par un panneau solaire.

Remarque : En toute rigueur il faudrait examiner si la batterie, supposée complètement chargée assure une autonomie suffisante pendant toute la nuit (absence de soleil).  Le lecteur est invité à établir une méthode de calcul pour vérifier l’autonomie de la batterie.

Quiz n° 3

Je dois prévoir une station radio HF ondes courtes de puissance appréciable (300 W RF) pour un Fielday de 24 heures.  Le transceiver nécessite un courant de 45 A sous une tension de 13,8 V lorsque celui-ci est en émission à pleine puissance.  J’estime la proportion du temps d’émission à 70 % de la durée du Fielday.  Je néglige la consommation de la station en réception.  Je dois me prononcer s’il vaut mieux alimenter la station à partir d’une batterie de grosse capacité avec un élévateur de tension 12 V vers 13,8 V d’un rendement de 90 % ou s’il vaut mieux prévoir un groupe électrogène 230 V 50 Hz avec une alimentation secteur 13,8 V à haut rendement de 90 %.

Questions :

• Quelle devrait être la capacité à prévoir pour une batterie de 12 V ?
• Quelle est la puissance nécessaire du groupe électrogène à prévoir ?
• Quel est votre avis : batterie ou groupe électrogène ?
• Subsidiaire : quel est l’âge de l’OM qui opère la station ?

Réponses et explications au quiz n° 3 :

Consommation énergétique de la station radio :

Calcul de la capacité de la batterie :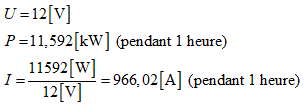

On constate après un rapide calcul auquel vous êtes maintenant habitué que la batterie à prévoir doit avoir une capacité de pratiquement 1000 Ah (théoriquement de 966,02 Ah).  Est-ce bien raisonnable de prévoir une batterie d’une telle capacité ?

Ce qu’il y a moyen de faire, c’est de constituer un jeu de quatre batteries de 250 Ah chacune.  Soit on les utilise l’une après l’autre : quand une batterie est vide, on la remplace par la suivante.  Soit on dispose de quatre batteries de 250 Ah toutes du même type, du même constructeur, de la même date de construction et toutes dans le même état de charge.  Dans ce cas, on raccorde les quatre batteries de 250 Ah en parallèle pour obtenir une capacité totale de 1000 Ah.

Dimensionnement du groupe générateur :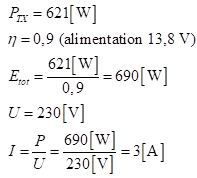

La puissance disponible nécessaire doit être de 690 W.  On doit donc, en pratique, prévoir un groupe électrogène de 1 kVA.

Quiz n° 4

J’ai finalement prévu un groupe électrogène de 1 kVA pour la station HF du Fielday.  Le courant secteur (d’une tension de 230 V) qui est nécessaire pour l’alimentation 230 V/13,8 V du transceiver est de 3 A.  Pour éloigner le plus possible le groupe électrogène de la station radio, je prévois un enrouleur de câble complètement déployé d’une longueur de 50 m et dont la section des conducteurs est de 2,5 mm².

Question :

Quelle sera la chute de tension dans le câble de l’enrouleur ?

Réponses et explications au quiz n° 4 :

La longueur totale du conducteur de section de 2,5 mm² établissant le circuit fermé entre le générateur et la prise secteur de l’alimentation du transceiver est de 2 x 50 m = 100 m (aller et retour dans le câble).

On peut calculer la résistance linéique d’un conducteur d’une section de 2,5 mm² par la loi de Pouillet en connaissant la résistivité du cuivre à 300 K ou bien on peut tout simplement consulter une table de la résistance linéique des conducteurs des sections normalisées et usuelles pour des applications électriques.

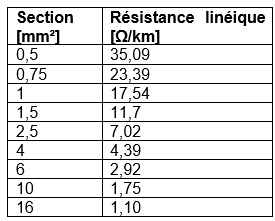
Un conducteur de 100 m et d’une section de 2,5 mm² a donc une résistance de 0,702 Ω.

Chute de tension sous un courant de 3 A :

U = 0,702 Ω x 3 A = 2,1 V.  Ce qui est négligeable vis-à-vis d’une tension secteur de 230 V.

Conclusion :

Ces quatre quiz et les questions qui les accompagnent permettent de soulever certains aspects pratiques dans l’alimentation d’une station radio en toutes circonstances.  Il est parfois intéressant de connaître les raisons physiques qui expliquent d’où proviennent les recettes empiriques que nous utilisons dans certaines de nos réalisations OM’s.

En espérant que ce QUIZ vous a été utile.

Vignette : ON5VL - ONFF+ https://www.clipartmax.com

Cet article peut être téléchargé au format PDF. Il suffit de cliquer sur ce lien :

A propos de l'auteur