Le B.A. BA de la Ligne d’Alimentation (Suite et fin)

Nous avions terminé la première partie par un exemple chiffré qui montre une image peu réjouissante du R.O.S qui dans la pratique courante d’un système d’antenne bien pensé est très différente.

Nous allons examiner plus en détail les éléments qui entrent en ligne de compte pour assurer autant que possible le rendement optimal de la puissance électrique transmise à l’antenne.

Le but étant de regarder le dessous des cartes pour comprendre ce qu’il s’y joue, je ne vais pas me limiter à dérouler l’un ou l’autre « User Guide » d’outils informatiques en relation avec le sujet, qui bien que très utiles dans la pratique courante, occultent les mécanismes sous-jacents nécessaires à une bonne compréhension.

Table des matières :

1. Principes généraux de l’adaptation d’impédances
            1.1 Quand la puissance est-elle maximale à la charge RL ?
            1.2 Adaptation d’impédances en HF
                       1.2.1 Exemple de l’adaptation entre deux résistances au moyen d’une réactance

2. La Puissance réfléchie est-elle une puissance perdue ?
           2.1 La ligne sans perte est adaptée à sa sortie
           2.2 La ligne sans perte est désadaptée à sa sortie
                        2.2.1 La ligne est également désadaptée à son entrée
                        2.2.2 La puissance réfléchie s’ajoute à la puissance réduite fournie par le générateur
           2.3 Une adaptation d’impédances est installée.

3. L’adaptation conjuguée
           3.1 Théorème de l'adaptation conjuguée.
           3.2 Une adaptation conjuguée existe à travers l'ensemble du système
           3.3 Une ré-réflexion précise et totale de l’onde réfléchie.

4. L’onde réfléchie détériore l’amplificateur final ?
5. Augmentation de la puissance incidente résultant d'une adaptation conjuguée à l'entrée d'une ligne de transmission désadaptée en sortie.
          5.1 La ligne de transmission est sans perte.
          5.2 La ligne de transmission présente des pertes (atténuation).

1. Principes généraux de l’adaptation d’impédances
Dans un circuit électrique quelconque, constitué d'un générateur de FEM E d'impédance interne Z_S, relié à une charge Z_L, le concepteur recherche le plus souvent à ce que la charge reçoive la puissance maximale que le générateur est capable de fournir.

Prenons un circuit électrique composé de simples résistances, le courant débité par le générateur de tension de FEM E est :  I= E /(R_S + R_L)
La puissance développée par le générateur est : P= E.I
La puissance délivrée par le générateur est fonction du courant I.
La puissance disponible à la charge est : P= R_L.I²
La puissance dissipée dans la résistance interne du générateur est : P= R_S.I²

En considérant comme invariables la FEM E et la résistance interne RS du générateur :
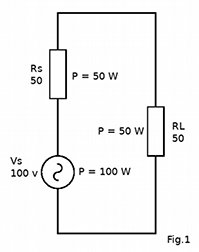
- quand la charge RL est élevée, le courant I est faible et la puissance produite par le générateur est faible Fig.2.
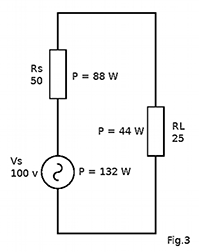
- inversement, quand la charge RL est faible, le courant I est élevé et la puissance produite par le générateur est élevée Fig.3
En comparant les Fig.2 et Fig .3 la puissance produite par le générateur est doublée pour la même puissance disponible à la charge RL.
Conclusion : le générateur adapte la puissance produite en fonction de la valeur de la charge.

1.1 Quand la puissance est-elle maximale à la charge RL ?

Le calcul simple au moyen de la loi d’Ohm, du courant résultant dans les trois configurations ci-dessus nous conduit à constater que la puissance maximale disponible à la charge est celle qui se  produit quand la résistance de charge est égale à la résistance interne du générateur [*]. Dans la situation de la Fig.1, le rendement est de 50 %, la moitié de la puissance produite par le générateur de tension est dissipée dans sa résistance interne et l’autre moité dans la résistance de charge.
Dans les deux autres configurations, où la résistance de charge est soit le double,soit la moitié de la résistance interne de la source, la puissance disponible à la charge est inférieure. Remarquons aussi dans la Fig.3 que la plus grande partie de la puissance produite par le générateur de tension est dissipée dans sa résistance interne.
Note : Ici il n’est pas tenu compte du rendement du générateur, c’est-à-dire du rapport de la puissance à la charge par la puissance produite par le générateur. La Fig.2 montre un meilleur rendement que les deux autres configurations, bien que la puissance à la charge soit moindre que la puissance maximale disponible.
[*] En mathématique cette condition de RL=RS pour une puissance maximale dans RL se démontre facilement en égalant à zéro la dérivée première par rapport à RL de la fonction

1.2 Adaptation d’impédances en HF

En courant alternatif cette adaptation, RL=RS, est exclusivement réalisée au moyen de composants réactifs qui, s'ils sont parfaits, ne sont pas consommateurs d'énergie. Le but étant de présenter au générateur, avec un minimum de perte, une impédance égale à sa résistance interne de manière à obtenir le maximum de puissance à cette impédance.
Il existe de nombreux agencements de réactances capables de réaliser cette fonction d'adaptation, dont les trois principaux sont les circuits en « L inversé », en  « Pi » et en « T ».
Les radioamateurs connaissent bien ou ont souvent entendu parler des circuits en Pi et en T.
Les circuits d’adaptation faisant partie intégrante de nos lignes d’alimentation, et de nos émetteurs nous allons montrer par une brève analyse l’adaptation d’impédance au moyen d’un circuit en L inversé qui est le circuit de base des autres formes de circuit, hormis les circuits faisant intervenir une transformation par couplage magnétique.

** Le paragraphe 1.2.1 n’est pas indispensable à la compréhension de la suite du sujet, bien qu’ouvrir le « moteur » peut grandement aider à comprendre le mouvement des pistons. Il est montré simplement qu’un circuit d’adaptation d’impédances n’est rien de bien compliqué si l’on aime manipuler de simples équations de nombres complexes. Sachant que l’ »Abaques de Smith », s’il est bien compris, permet de résoudre graphiquement les situations des plus simples aux plus complexes.

1.2.1 Exemple de l’adaptation entre deux résistances au moyen d’une réactance
La principe et le calcul sont basés sur ce que l’on appelle une transformation de circuit.
1) Soit à calculer le circuit série Rs+jXs équivalent à un circuit Rp // jXp

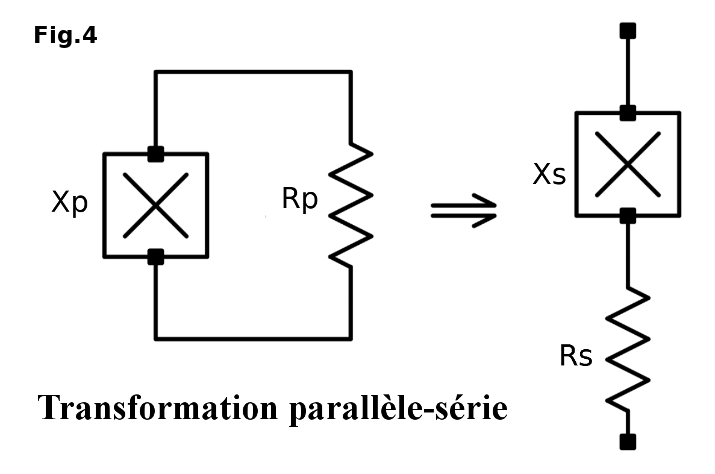
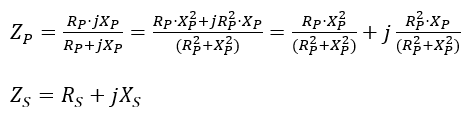
En égalant membre à membre les parties réelles et les parties imaginaires (réactives), on trouve :
et 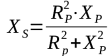en posant   et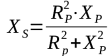

Avec une valeur de QP >>1, ce qui est généralement le cas, la valeur de la résistance série équivalente RS est inférieure à la résistance réelle RP et la valeur de la réactance série équivalente XS est approximativement égale à XP. C’est la configuration que l’on choisit pour « réduire » la valeur apparente d’une résistance.
Le schéma équivalent n’est alors plus une résistance pure, mais l’association en série de la résistance apparente RS souhaitée et d’une réactance résiduelle non désirée XS. Ce qui introduit une réponse en fréquence qui n’est plus plate, mais centrée sur la fréquence qui a été choisie pour déterminer la réactance parallèle Xp à partir d’un composant capacitif ou inductif. La largeur de bande à -3 dB est fonction de QP  avec  B=F0 / QP .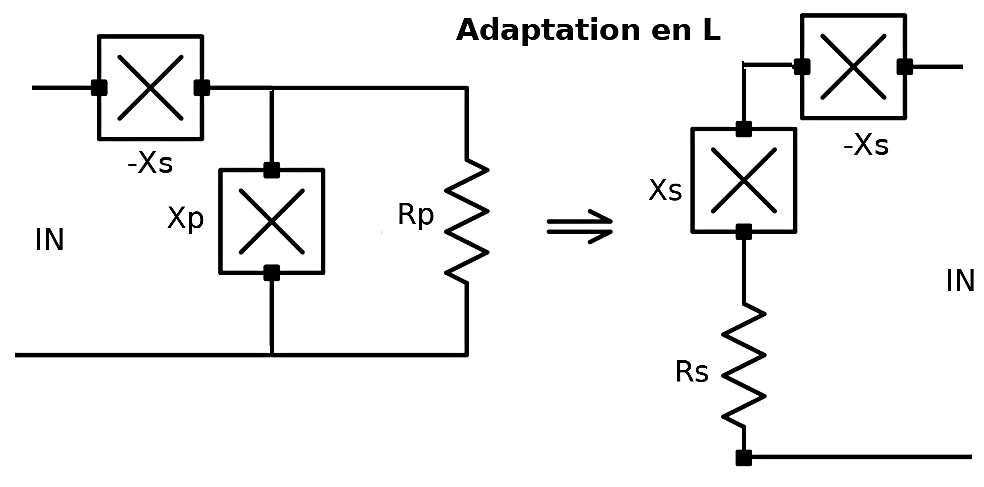
Dans une seconde étape, cette réactance série devra forcément être compensée par une réactance série de même amplitude mais de signe contraire de manière à obtenir la résonance, c-à-d une résistance pure.
Nous venons de réaliser notre premier circuit d’adaptation en L.
C’est en réalité ce que nous faisons en manipulant notre coupleur d’antenne, en premier lieu avec le contrôle de charge (Load) et ensuite avec le contrôle d’accord (Tune).

2) La seconde transformation possible consiste à calculer le circuit parallèle RP //jXP équivalent à un circuit série RS + jXS

 

 

 

 

En égalant membre à membre les parties réelles et les parties imaginaires (réactives), on trouve :

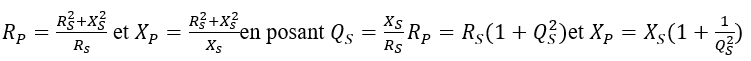
Avec une valeur de QS >>1, ce qui est généralement le cas, la valeur de la résistance parallèle équivalente RP est supérieure à la résistance réelle RS et la valeur de la réactance parallèle équivalente XP est approximativement égale à XS. C’est la configuration que l’on choisit pour « augmenter » la valeur apparente d’une résistance.

Ceci étant, dans notre domaine de la HF, le rapport tension/courant aux deux bornes d’un composant ou d’un circuit se traduit rarement comme une simple résistance ohmique, un rapport dans lequel la tension et le courant sont en phase.
Un générateur peut être confronté aux deux situations ci-dessous.

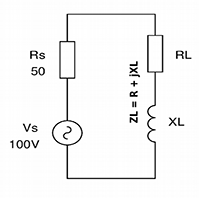
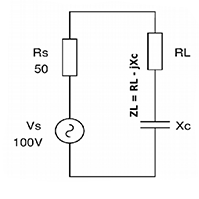
Comme nous venons de le voir, toute configuration de circuit peut être ramenée à son équivalent série soit directement, soit par étapes successives. Le rapport tension/courant que l’on nomme impédance Z, quelque soit la disposition matérielle originale des composants, est symbolisé sous la forme Z= R ± jX, le circuit série d’une résistance et d’une réactance. Dans laquelle R représente une résistance ohmique pure, où le courant et la tension à ses bornes sont en phase, et X représente une réactance, où le courant et la tension sont en quadrature (90°) de phase. Soit (+ j) si la tension est en avance de phase sur le courant comme aux bornes d’une inductance, soit (-j) quand la tension est en retard de phase sur le courant, comme aux bornes d’un condensateur.
Pourquoi prendre le courant comme référence de la phase ? Tout simplement parce que le courant est commun à tous les composants du circuit série.

2. La Puissance réfléchie est-elle une puissance perdue ?

2.1 La ligne sans perte est adaptée à sa sortie

Dans un premier temps, nous considérons une ligne d’alimentation sans perte ayant une charge terminale parfaitement adaptée ZL = Z0. La ligne est aussi adaptée à son entrée générateur-émetteur. Dans ces conditions, il n’y a pas de puissance réfléchie dans la ligne et de ce fait, pas de « perte » par réflexion. Le générateur délivre donc ce qui est défini comme la puissance maximale disponible à l’adaptation, et la charge absorbe toute la puissance délivrée.

2.2 La ligne sans perte est désadaptée à sa sortie (voir Le B.A. BA,... première partie)

Si maintenant la charge d’extrémité est modifiée, créant une désadaptation entre l’impédance caractéristique de la ligne Z0 et la charge terminale ZL, il y aura moins de puissance absorbée par la charge. La réduction de la puissance absorbée résultant du changement de l’impédance de la charge est la mesure de la « perte » par réflexion. Comme la puissance réfléchie retourne vers le générateur, elle provoque un changement de l’impédance Z0 de la ligne vers une impédance complexe Z=E/I et ce tout le long de la ligne.

Quand l’onde réfléchie atteint l’extrémité entrée de la ligne, le générateur-émetteur est confronté à un changement de l’impédance d’entrée depuis sa valeur caractéristique Z0 vers une nouvelle valeur déterminée par le rapport E/I en amplitude et en phase apparaissant aux bornes d’entrée de la ligne.

2.2.1 La ligne est également désadaptée à son entrée

Cette nouvelle impédance à l’entrée de la ligne présente exactement le même degré de désadaptation à l’impédance Z0 de la ligne que celui qui est généré par la charge terminale désadaptée ayant entraîné la réflexion.
Maintenant la ligne est désadaptée au générateur-émetteur à un même degré, et dans ces conditions, le générateur mettra automatiquement à disposition de la ligne moins de puissance, d’un niveau déterminé par la désadaptation. La réduction de puissance délivrée à l’entrée de la ligne est exactement de la même grandeur que la puissance réfléchie à la charge. En d’autres termes, la « perte » due à la  réflexion à la charge est reportée le long de la ligne vers le générateur. Donc cette « perte » par réflexion est simplement une perte non-dissipative représentant seulement moins de puissance fournie à la charge parce que le générateur délivre moins de puissance, conséquence de la désadaptation d’impédance à l’entrée de la ligne.
Il devient maintenant évident que la « perte » par réflexion représente seulement une diminution de puissance fournie à la charge, et que la charge absorbe toute la puissance que le générateur-émetteur met à disposition, à ce moment, à destination de la ligne.

2.2.2  La puissance réfléchie s’ajoute à la puissance réduite fournie par le générateur

Quand la puissance réfléchie par la charge atteint les bornes d’entrée, elle provoque la désadaptation au générateur-émetteur, désadaptation qui engendre à son tour une puissance réfléchie qui s’ajoute à la puissance réduite fournie par le générateur par exactement la même quantité de puissance que la diminution de puissance délivrée par le générateur-émetteur. Puisque à ce moment, la puissance incidente est égale à la puissance réduite du générateur augmentée de la puissance réfléchie, la puissance incidente atteignant la charge désadaptée demeure la même que celle avant que le générateur ne réduise sa puissance. Ainsi la perte par réflexion équivaut à la diminution de puissance mise à disposition par le générateur-émetteur. Cependant, puisque la puissance réfléchie par la charge est maintenant une partie de la puissance incidente atteignant la charge, la puissance incidente continue à être au même niveau que celle délivrée à l’origine par le générateur avant la diminution de sa fourniture. Donc la charge continue à recevoir la quantité original de puissance, et de ce fait absorbe toute la puissance réduite délivrée par le générateur.

2.3 Une adaptation d’impédances est installée.

Si une adaptation d’impédances est maintenant installée n’importe où le long de la ligne, même aux bornes d’entrée, la puissance réfléchie est empêchée de circuler en direction du générateur-émetteur au-delà du point d’adaptation. Donc, l’impédance caractéristique de la ligne entre le point d’adaptation et le générateur n’est dès lors plus concernée par l’onde réfléchie et elle demeure à sa valeur Z0 aux bornes d’entrée.  En conséquence le générateur ne voit plus une désadaptation et délivre à nouveau sa puissance nominale maximale à la ligne. L’adaptation d’impédance à donc généré une réflexion négative appelé communément un « gain de réflexion » qui égale exactement et annule la « perte » par réflexion.
En conséquence, toute la puissance effectivement délivrée par le générateur-émetteur est absorbée par la charge dans l’un ou l’autre cas de figure avec ou sans gain de réflexion. Le générateur délivre simplement moins de puissance avant que le gain de réflexion (l’adaptation) ne restaure la condition d’adaptation entre le générateur et la ligne.

3. L’adaptation conjuguée

D’après ce qui précède, la fonction première d’un réseau d’adaptation d’impédances est de provoquer une désadaptation ayant pour objectif la réflexion totale en retour des ondes réfléchies circulant de l’antenne vers l’émetteur tandis qu’elle présente une adaptation parfaite pour les ondes incidentes circulant de l’émetteur vers l’antenne. C’est le concept de base du fonctionnement du réseau en Pi ou en T pour adapter l’impédance de charge ZL présentée à la sortie de l’émetteur RF à son impédance de source Zs.
Notre réseau d’adaptation possède donc deux interfaces, une interface vers la sortie de l’émetteur et la seconde interface vers l’entrée de la ligne d’alimentation, c’est un quadripôle. 

3.1 Théorème de l'adaptation conjuguée.

Une adaptation conjuguée existe chaque fois que toute la puissance disponible (le maximum dont est capable la source) est délivrée à la charge. (Réf 137.IEEE)

Si un groupement de réseaux quadripôles contenant uniquement des réactances pures sont organisés en cascade pour connecter un générateur à une charge, alors si à n’importe quelle jonction, il existe une adaptation conjuguée des impédances, il y aura une adaptation conjuguée des impédances à toutes les autres jonctions dans le système. (Communication Engineering, Everitt-Anner, 1956 page 407)

3.2 Une adaptation conjuguée existe à travers l'ensemble du système

Toute la puissance disponible sera délivrée, c-à-d la puissance maximale dont est capable la source, quand l'impédance d'entrée de la ligne est rendue égale à la composante « résistive » (réelle ) de l'impédance de sortie de la source, et quand toutes les composantes réactives (imaginaires) dans les impédances de sortie de la source et d'entrée de ligne sont annulées (réduites à zéro) par un réseau d’adaptation. Le circuit d’adaptation peut être le circuit en Pi de sortie de l'émetteur, un circuit extérieur tel qu'un coupleur d'antenne (Antenna Turner Unit) ou les deux à la fois.
Dans cette configuration, l'ensemble du circuit est résonnant, incluant le circuit de sortie de l'amplificateur. Toute la puissance disponible à la source pénètre dans la ligne et les réflexions en provenance de n'importe quelle désadaptation ou autre discontinuité de ligne, en n'importe quel endroit, sont compensées par une nouvelle réflexion qui annule, au point d'adaptation choisi, la réflexion originale.
Une telle réflexion est obtenue en introduisant une désadaptation non-dissipative à l'endroit de la ligne choisi pour l'adaptation. Cette désadaptation non-dissipative, est celle qui placée dans le système devrait générer par elle-même une réflexion ou un S.W.R du même ordre de grandeur que celui produit par l'extrémité désadaptée.

3.3 Une ré-réflexion précise et totale de l’onde réfléchie.

Bien que cela semble très compliqué, l'ensemble des conditions est automatiquement réalisé en effectuant simplement une procédure d'accord (Tune) et de charge (Load) de la source de puissance (l'émetteur).
Si l'émetteur ou le générateur de source est maintenant remplacé par une impédance passive égale à son impédance de source (égale à sa résistance de charge optimale) la ligne peut être ouverte en n'importe quel endroit.  Ensuite, à partir de cette ouverture et en regardant dans l'un et l'autre sens, nous verrons l'impédance conjuguée de l'impédance vue dans la direction opposée, que la valeur   soit vue dans une direction,  sera vue dans l'autre direction.

Quel que soit le type de réseau d’adaptation utilisé, l’adaptation est réalisée parce que le réseau lui-même présente une désadaptation complémentaire qui génère une autre réflexion de l’onde, complémentaire à celle à générée à l’extrémité désadaptée. Ces deux ondes réfléchies complémentaires sont des images miroir l’une de l’autre, parce qu’elles ont la même amplitude, mais sont opposées en phase (déphasées de 180°). La nature complémentaire des ondes, courant et tension, générées par le réseau d’adaptation est obtenue en sélectionnant des valeurs appropriées pour les composants du réseau. Quand les deux ondes réfléchies de phases opposées se rejoignent au point d’adaptation dans le réseau, elles s’annulent mutuellement. Cette annulation crée un circuit virtuel ouvert ou fermé (zéro courant ou zéro tension) pour les ondes circulant en retour, et provoquent leur totale re-réflexion - une inversion totale de leur direction arrière. Les ondes s’additionnent alors en phase avec l’onde de source, produisant une onde résultante circulant dans la direction avant.

Note: L’assimilation du circuit d’adaptation au comportement d’une ligne d’alimentation ouverte ou en court-circuit à l’interface coté émetteur a fait l’objet dans un passé pas si lointain, d’un échange assez pointu entre deux spécialistes appréciés internationalement qui ne partagent pas exactement la même compréhension du processus d’adaptation.
Sans entrer dans le débat et prendre parti pour l’un ou l’autre, ce sont plutôt les conséquences qui nous intéressent ici.
Comme radioamateurs notre coupleur d’antenne nous permet d’empêcher la puissance réfléchie de poursuivre son chemin jusqu’à l’émetteur. C’est que nous constatons après réglages, par la lecture du R.O.S mètre intégré à la sortie émetteur du coupleur d’antenne. Si nous plaçons un second mesureur de R.O.S. à la sortie antenne du coupleur, nous pouvons constater que la puissance incidente vers l’antenne est supérieure à la puissance incidente indiquée par le R.O.S. du coupleur. De là nous pouvons simplement déduire que la puissance réfléchie par l’antenne retourne totalement à l’antenne sans intervention autre que les circuits réactifs du coupleur considérés sans perte. Voir les paragraphes 5.1 et 5.2 pour plus de détails. 

4. L’onde réfléchie détériore l’amplificateur final ?

Contrairement à ce que beaucoup croient, il n’est pas vrai que quand un émetteur délivre de la puissance dans une ligne sujette à réflexions, une onde réfléchie en retour voit la résistance interne du générateur comme une charge dissipative. Pas plus que l’onde réfléchie est convertie en chaleur et perdue, tandis qu’en même temps elle détériore l’amplificateur final.
Quand un amplificateur de puissance RF, adapté à sa charge, fournit activement de la puissance au moment où l'onde réfléchie revient, elle subit une nouvelle réflexion totale au point d'adaptation se situant aux bornes d'entrée du circuit d'adaptation (coté émetteur) et la puissance réfléchie est entièrement conservée parce qu'elle ne voit jamais l'impédance de source de l'amplificateur comme une charge terminale dissipative, et pas plus parce que l'impédance de source serait non dissipative.
Les tensions réfléchies et de source ainsi que les courants respectifs se superposent ou s’additionnent (en phase) au point d’adaptation, exactement comme si la puissance réfléchie avait été fournie  par un générateur séparé en série avec la source. Le vecteur somme des tensions produit une circulation du courant résultant qui est toujours dans la direction avant. La puissance réfléchie s’additionne donc à la puissance de la source se traduisant comme un gain de réflexion, lequel compense la perte due à la  réflexion subie à l’extrémité désadaptée.

5. Augmentation de la puissance incidente résultant d'une adaptation conjuguée à l'entrée d'une ligne de transmission désadaptée en sortie.

Quand nous utilisons une ligne de transmission coaxiale avec une charge non adaptée qui génère des ondes stationnaires sur la ligne, nous devons être attentif aux limites qui sont imposées à l'amplitude des ondes stationnaires par rapport aux capacités en tension et en puissance de la ligne. Nous devons donc trouver un moyen pour déterminer le niveau de puissance circulant sur la ligne en fonction de l'amplitude des ondes stationnaires.
Il n’est pas toujours connu qu’une ligne de transmission désadaptée à sa charge, mais adaptée de manière conjuguée à son entrée, (ex : un coupleur d'antenne), voit la puissance incidente (directe) se propageant le long de la ligne être supérieure à la puissance fournie par la source d'un montant égale à la puissance réfléchie.
En conséquence, pour ce qui concerne les lignes sans pertes, la puissance absorbée par l'extrémité non-adaptée est égale à la puissance incidente totale diminuée de la puissance réfléchie, différence qui représente la puissance effectivement délivrée par la source. Pour que ce phénomène se produise, la puissance circulant dans la sens direct doit forcément dépasser celle fournie par la source. 

5.1 La ligne de transmission est sans perte.

Quand une onde d'énergie (tension, courant) est appliquée dans un premier temps à l'entrée d'une ligne de transmission, elle voit seulement l'impédance caractéristique ZC dans son déplacement le long de la ligne jusqu'à ce qu'elle arrive à l'extrémité désadaptée.
En arrivant à la désadaptation, l'onde est réfléchie avec une amplitude qui dépend du coefficient de réflexion
avec
             ρL= coefficient de réflexion en tension et en courant à l'extrémité désadaptée.
             ZC= l’impédance caractéristique de la ligne
             ZL= l’impédance de la charge à l'extrémité de la ligne, avec  Z_L ≠  Z_C

Sachant que 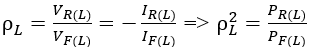comme c'est la puissance qui fait l'objet de cette  analyse, nous retiendrons  uniquement

Pour améliorer la lisibilité des équations, nous appliquons la substitution suivante ρL² = a .

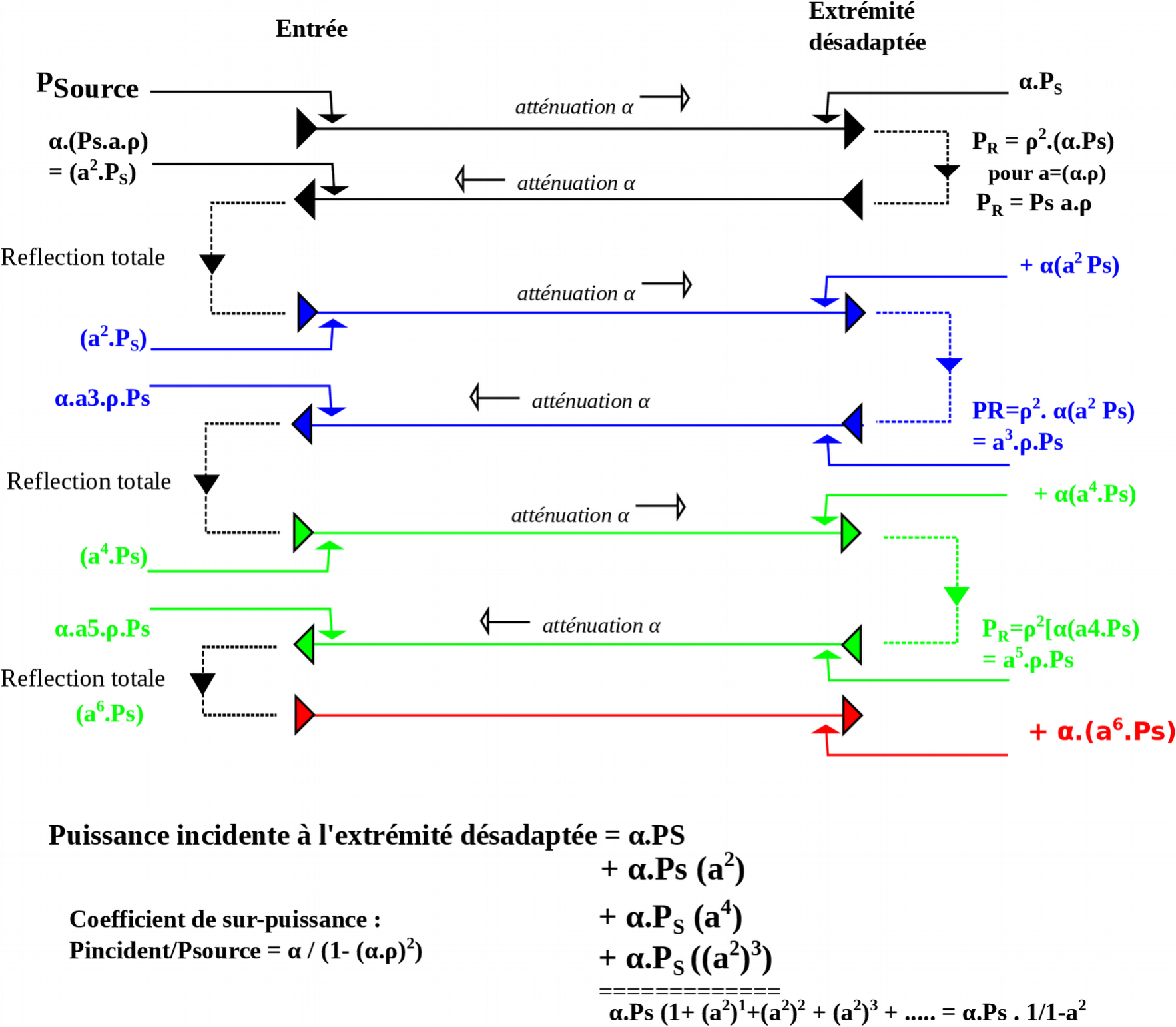
Dans la figure ci-dessous, nous illustrons uniquement le comportement de la puissance réfléchie, tout en sachant qu'une fois arrivée à l'entrée de la ligne, elle se combine à chaque retour avec la puissance en provenance de la source.

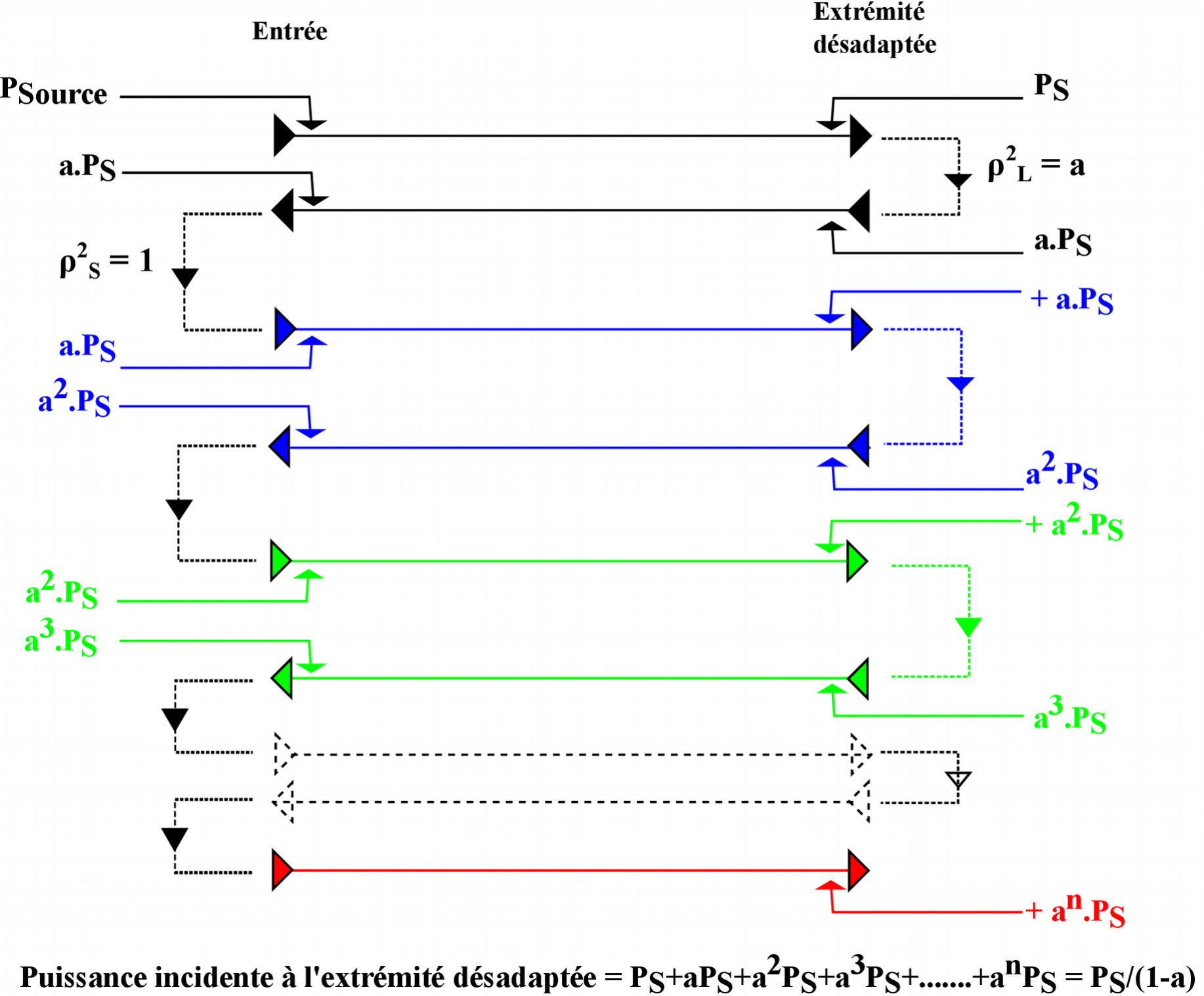
1) La réflexion de la puissance incidente [PF(L) = PS] à l'extrémité désadaptée donne naissance à une puissance réfléchie PR1 qui se déplace en retour vers l'entrée de la ligne avec une amplitude déterminée par le produit de [ρL²] par la puissance incidente : [PR1 =  ρL² x PS = a x PS] .
2) En arrivant à l'entrée de la ligne, PR1 subit une réflexion totale [ρS² = 1] au point d'adaptation (entrée émetteur) que réalise l'adaptation conjuguée (coupleur d'antenne).
Cette réflexion de PR1 à l’entrée constitue une deuxième puissance incidente de même amplitude qui circule vers l'extrémité désadaptée [PR2 = PR1 = a PS] en phase avec la puissance fournie par la source.
3) Cette puissance une fois arrivée à l'extrémité désadaptée est à nouveau réfléchie vers l'entrée de la ligne avec une amplitude liée à [ρL²] : [PR3 = PR2 x a = a² PS]
4) Arrivée au début de la ligne, PR3 rencontre la toujours présente réflexion totale [ρS²= 1] et se retrouve une fois de plus renvoyée vers l'extrémité désadaptée avec une amplitude identique et toujours accompagnée de la puissance générée par la source: [PR4 = PR3 =a² PS]
5) A l’extrémité désadaptée, cette troisième puissance incidente PR4 est à son tour réfléchie vers l'entrée de la ligne : [PR5 = PR4 x a = a³ PS]
6) ……..
Ce fonctionnement continue indéfiniment avec pour chaque puissance réfléchie incidente une amplitude inférieure à la précédente car : [0 < ρ < 1] [ρ²  << 1] , [a << 1 ]
Cette progression géométrique [Ptot = PS (1+a+a²+a³+a⁴+...+aⁿ] de raison [a < 1] dont la somme est convergente représente la condition de l’état stable qui est finalement atteint.
La série infinie [1+a+a²+a³+a⁴+...+aⁿ] converge vers la valeur avec [|a| < 1] [*] .
[*] Voir Mathématiques Supérieures, Suites et Séries.
En revenant à la substitution inverse pour [a] =>

Expliqué de manière plus succincte

Par un développement itératif nous voyons à chaque aller-retour à la charge que la puissance incidente est la somme de la puissance fournie par la source additionnée en phase avec la précédente puissance réfléchie, qui est alors totalement re-réfléchie à l’entrée de la ligne
Nous avons l’expression générale P_incidents = P_source + P_réfléchie  qui nous donne successivement :

1er aller-retour :  P_incidentes = P_source + (P_source x P²) = P_source (1 + p²)
pour le second retour vers la source : p_réfléchi2 = (P_incidents x p²) = (P_source(1 + p²)) x p² = P_source  x (p² + p⁴)
2e aller-retour : P_incidente = P_source(1 + (p²)¹ + (p²)²)
3e aller-retour : P_incidente = P_source(1 + (p²)¹ + (p²)²) + (p²)³
4e aller-retour : P_incidente = P_source(1 + p² + p⁴ + p⁶ = p⁸)
Soit une série infinie de raison ρ² qui converge vers la limite finie

En régime permanent, la puissance totale se propageant dans la direction de la charge désadaptée, quand la ligne est adaptée-conjuguée à l'entrée à l'aide d'un réseau d'adaptation tel qu'un coupleur d'antenne est donnée par :  s'appelle le facteur d'accroissement de la puissance d'entrée.

Tandis que 1 - p² s'appelle le coefficient de transmission de puissance :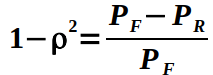

qui représente le pourcentage de la puissance incidente qui est absorbée par la charge désadaptée .

Exemple :
Soit un émetteur de 50 W qui alimente une antenne d’impédance d’entrée résistive de 150 Ω au moyen de 30 m de ligne d’alimentation d’impédance caractéristique 50 Ω. La ligne ne présente pas de pertes (atténuation).

Le R.O.S. :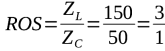

Le coefficiant de réflexion en tension :

Le coefficiant de réflexion en puissance :

La puissance incidente à l'antenne : 

La puissance réfléchie à l'antenne :

La puissance absorbée par l'antenne :

Toute la puissance fournie par l’émetteur, excepté une perte éventuelle dans le coupleur est disponible aux bornes de l’antenne et ce quel que soit le R.O.S sur la ligne d’alimentation.

C’est la raison pour laquelle, nos anciens qui utilisaient des lignes d’alimentation en échelle à grenouilles, à perte dérisoire, n’étaient pas sensibilisés par le R.O.S. qui pouvait exister sur la ligne une fois réglé le filtre en Pi de sortie du PA à tubes. Le R.O.S et son mesureur le R.O.S. mètre tel que nous le connaissons a fait sont apparition et sa réputation en même temps que l’arrivée du câble coaxial après la WWII.

5.2 La ligne de transmission présente des pertes (atténuation).

Nous suivons la même procédure en réduisant la valeur de [ρ] par l'atténuation [α]
Pour améliorer la lisibilité des équations, nous appliquons la substitution suivante  [a = α x ρL]  .

La série infinie (1 + (a²)¹ + (a²)² + (a²)³ +.... +(a²)ⁿ) converge vers   avec |a|<1 .

La série infinie [1+a+a2+a3+a4+...+an]  converge vers la valeur  avec [|a| < 1] [*] .

 En revenant à la substitution inverse pour a => 

En régime établi, la puissance à l’extrémité désadaptée est :

Le rapport du coefficient de « sur-puissance » de la ligne avec atténuation par rapport à la ligne

 sans atténuation :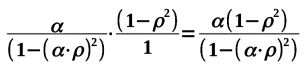

Exemple :

Soit un émetteur de 50 W qui alimente une antenne d’impédance d’entrée uniquement résistive de 150 Ω au moyen de 30 m de ligne d’alimentation d’impédance caractéristique 50 Ω. Suivant les spécifications du constructeur, la ligne présente une atténuation de 0.42 dB pour 30 m à 14 MHz.

Nous constatons ici que le R.O.S couplé à l’atténuation à l’adaptation de la ligne introduit une perte supplémentaire d’un peu plus de 2 W soit 5 % dans le cas présent.

L'atténuation de 0,42 dB donne :

La puissance à l'antenne :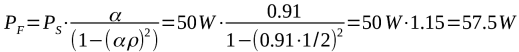

La puissnace réfléchie à l'antenne :

La puissance absorbée pr l'antenne :

Avec une charge adaptée la puissance à  l'antenne aurait été de :

Conclusion

Dans un système d’antenne avec une ligne d’alimentation désadaptée à l’extrémité antenne, mais adaptée par un ATU à l’extrémité émetteur, le R.O.S intervient principalement comme un coefficient multiplicateur de l’atténuation à l’adaptation de la ligne.

Pour des lignes de bonne qualité présentant aux basses fréquences HF une faible atténuation à l’adaptation, un R.O.S. élevé sur la ligne entre le coupleur et l’antenne peut ne pas être trop impactant comme nous venons de le voir dans l’exemple ci-dessus.

Par contre sur les fréquences VHF-UHF, où l’atténuation à l’adaptation de la ligne est souvent beaucoup plus élevée, le radioamateur a intérêt à adapter au plus près l’impédance de l’antenne à celle de la ligne pour éviter tout R.O.S sur la ligne d’alimentation.

A la lecture de cet exposé vous avez pu constater l’aspect répétitif de certaines notions qui loin de vouloir ennuyer le lecteur n’a pour objectif que d’assoire une compréhension précise et sans ambiguïté des mécanismes internes d’une ligne d’alimentation désadaptée.

Meilleurs 73s et excellents QSOs TECHNiQUES.

Le lien pour télécharger cet article au format PDF :

A propos de l'auteur